傅里叶指数形式简析

根据欧拉公式

可得

其中,

【例1.1】 试求图1.8所示的周期性方波的频谱。

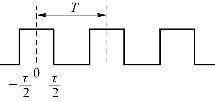
图1.8 周期性方波

解:设周期性方波的周期为T,方波的宽度为τ,幅度为1。

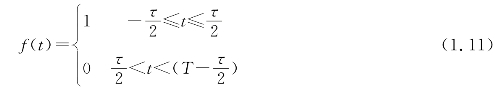
求频谱:

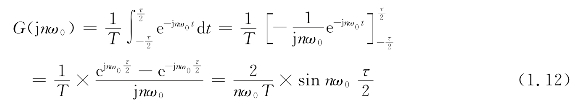
画出频谱图,如图1.9所示。(www.xing528.com)

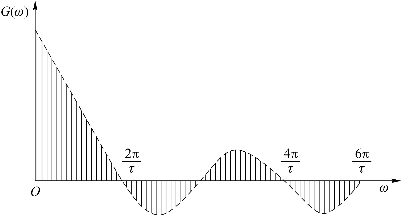
图1.9 周期性方波的频谱图

由图1.9可以看出,周期信号的频谱函数是由一系列的离散谱线构成的。它的频谱是离散谱,两谱线的间隔为脉冲重复周期越大,谱线越靠近,但其包络仍是形。当(m=1,2,3,…)时,谱线包络经过零点。

周期性方波信号包含无穷多条谱线,但其主要能量集中在第一个零点以内,通常把在第一个零点以内的频率范围称为周期性方波信号的频带宽度。

或

如果T保持不变,τ为不同时,由图1.9可见,脉冲越窄,频带越宽。

在的特殊情形下,矩形脉冲序列成为交替开关方波,通过周期函数的频谱变换,其傅里叶级数可写成

这时,信号仅包含直流和基波及奇次谐波,而谐波的幅度与频率成反比。如矩形脉冲序列成为双极性交替开关方波,正的幅度为1,负的幅度为-1,那么傅里叶级数没有直流分量,而基波和奇次谐波幅度比以前加倍,即

如果脉冲宽度τ保持不变,脉冲间隔T加得很大,则频谱线的数目加得很多,它们的包络依然是sin x/x形。最后,到了极限,T变成无限大,信号成为单个矩形脉冲时,则具有连续的sin x/x形频谱。这时,傅里叶级数变成非周期信号傅里叶变换,就是1.3节的情形。