伺服变量机构实质上是一个由双边滑阀控制的差动缸组成的动力机构,它的工作原理如图2-18所示,可供分析其特性用。假设阀为理想零开口三通滑阀,对应于阀芯位移和阀压降变化的流量变化能瞬时发生,并忽略所有的泄漏。各物理量的正方向如图2-18所示,对控制腔应用连续方程,得
qL=Kqxv-Kcpc (2-12)
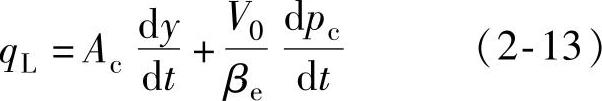
式中 Kq——伺服阀的流量增益;
Kc——伺服阀的流量压力系数;
pc——变量活塞控制腔大腔控制压力;
xv——阀芯开口量;
Ac——变量活塞大端面积;
V0——控制腔容积;
βe——油液的体积弹性模数;
y——变量机构输出位移。
活塞方程和负载的受力方程为
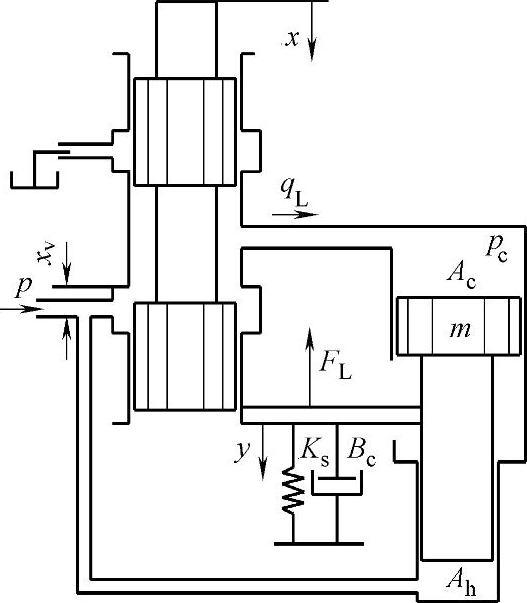
图2-18 位移直接反馈比例排量调节机构简图
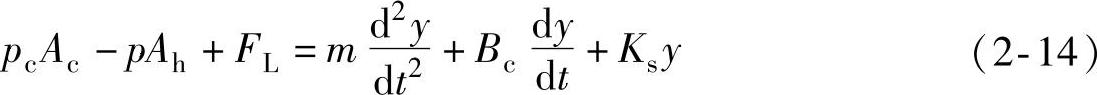
式中 Ah——活塞小端面积;
p——泵的出口压力;
FL——变量机构的负载力;(https://www.xing528.com)
m——变量机构的运动部件的质量;
Bc——黏阻系数;
Ks——弹簧负载刚度。
对式(2-13)和式(2-14)利用小变量线性化理论进行线性化处理,并对它们进行拉氏变换可得

pcAc-pAh+FL=mS2Y+BcSY+KsY (2-16)
式中 S——拉普拉斯算子;
m——活塞质量。
在式(2-14)中由于p为泵的出口压力,在变化过程中不一定是恒量,所以研究泵的动态特性时不应将其忽略。
对式(2-12)也进行拉氏变换,并利用式(2-15)和式(2-16)经运算后求得
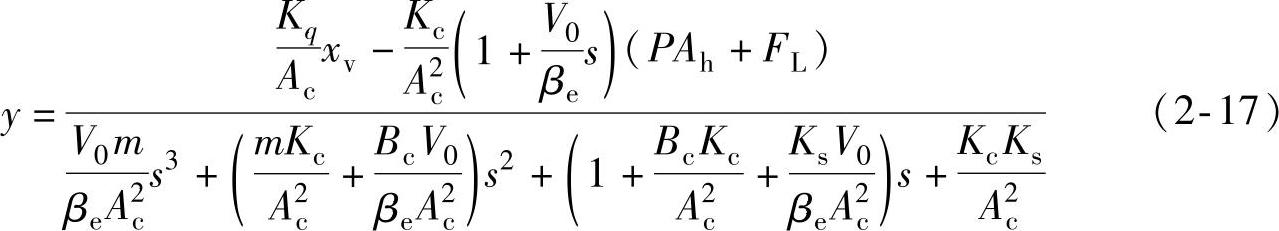
变量活塞的弹性负载刚度Ks主要是由变量泵供油回路的连接情况而确定的,在输入信号变化较慢时,可以认为弹性负载刚度为零。而当变量信号变化较快,特别是快速双向变化时,则弹性负载刚度的影响不容忽视。
经简化,最终可以写出活塞对阀位移的传递函数为
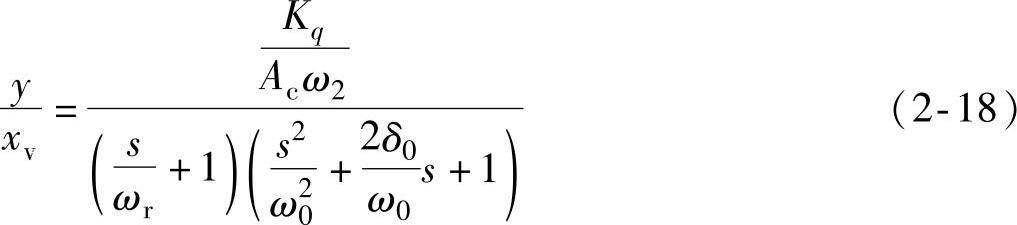
式(2-18)中的δ0、ω0、ω1、ω2、ωr的表达式如下:
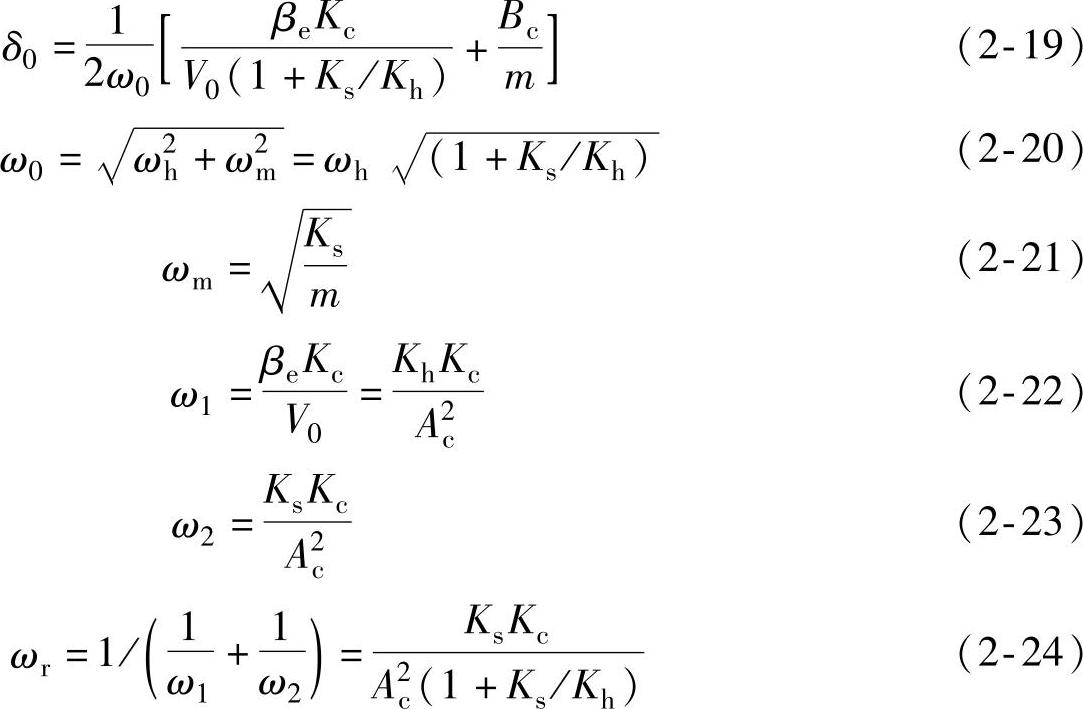
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




