体积弹性模量、可压缩性系数和液容的探究

一个充满油液的液压缸如图1-4所示：移动活塞可以改变液体的容积，通过活塞使原始压力p₀增加一个Δp的增量，原始体积V₀=Al₀则被减少了一个ΔV_Fl，因为压力流体是可压缩的，考虑到由于压力增大时体积减小，因此式（1-1）右边需加一负号，以使压缩系数为正。因此有

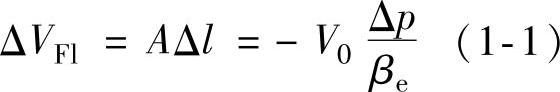
体积弹性模量β_e（单位为N/m²）可用下式表示

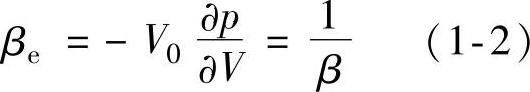
体积弹性模量的倒数β（单位为m²/N）称为可压缩性系数

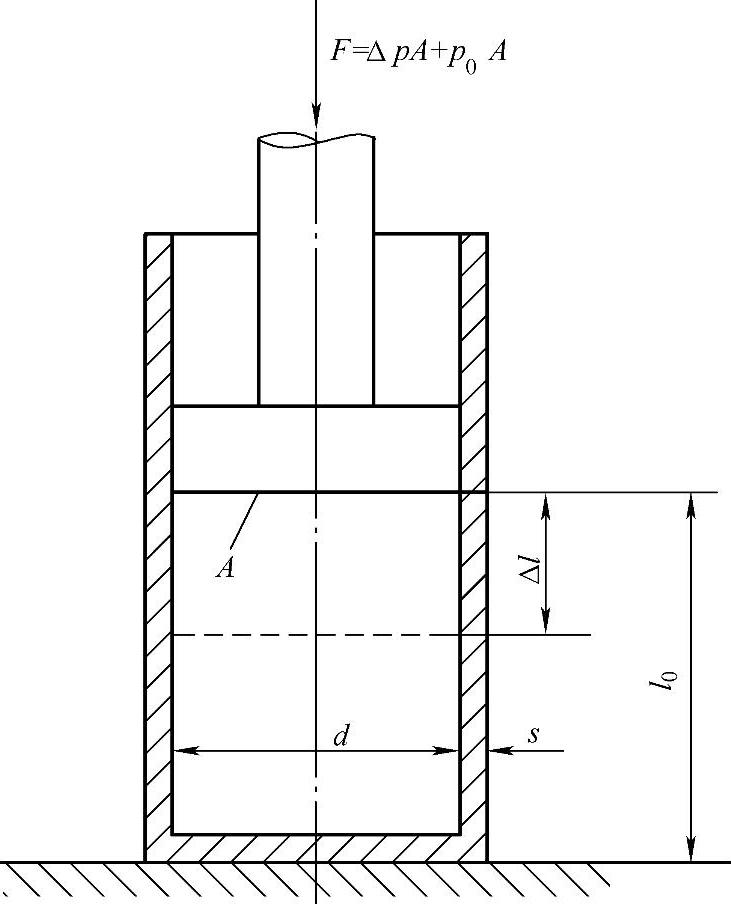
图1-4 液体容积的可压缩性

对式（1-1）微分可得到可压缩性液体的流量q_k，其正比于压力变化率p

比例系数C_H称为液容：

体积弹性模量β_e不是一个常数，其取决于各种变参数，如压力、温度和未溶解在压力油中空气的含量。此外，容器壁的弹性影响体积弹性模量。为了确定该模量，常用考虑所有这些影响的等效体积弹性模量β′_e计算。那么液容表达式变成：

βe在普通的温度和压力范围下可以近似认为是常量，对于基于矿物油的压力流体，它等于

βe≈1.6×10⁹N/m²=16MPa(www.xing528.com)

充满一台液压缸，一根管道或者其他容器的液体的可压缩性是随着容器壁的弹性变小和液体内的气泡增加而增加的，有效体积弹性模量因此会减小。假如一薄壁管道的内压增加了Δp，那么根据Barlow公式得到

这里V_R是原始的体积，E_R是管道材质的弹性模量（杨氏模量），d是管道的内径而s是管道的壁厚，管道延伸引起的体积的增加由管道的横向收缩引起的体积减少而补偿，因此简化的式（1-7）适用于所有泊松数接近0.3的金属管道。

在一个厚壁管道中随着压力增加一个Δp，体积的变化为

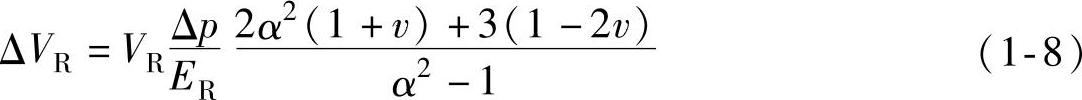
式中 α——管道外径和内径之比。

v——油液在管道中的流速。

类似于式（1-2），考虑容器壁弹性变形的影响，等效体积弹性模量β_e′，对于充满油液的管道被定义为

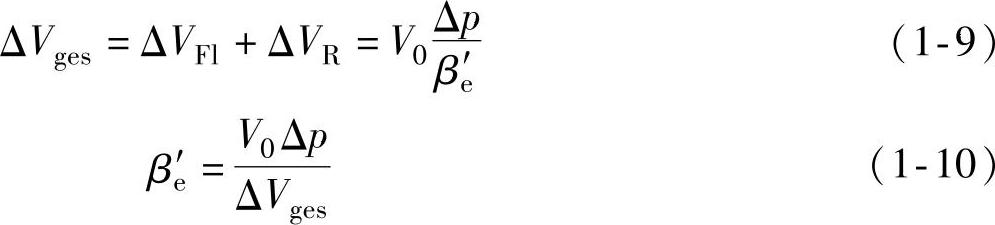
对于薄壁充满油液的管道得到如下公式：

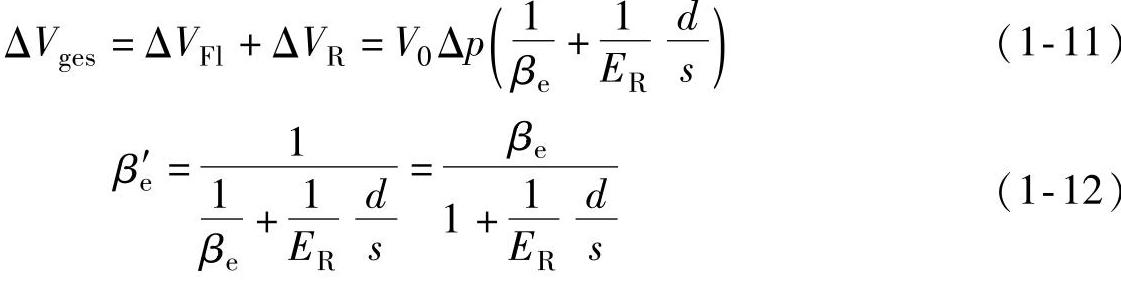
高压管道由于壁厚很大，对等效体积弹性模量的影响很小，但对于薄壁管道特别是软管应该考虑其影响。

假如未溶解的空气存在于压力流体中，其对可压缩性会产生严重的影响。空气溶解过程取决于气泡的尺寸和其可能作用的时间。因此，假如需要计算确切的液压系统的等效体积弹性模量的值，应该在实验条件下进行。

在液压缸封闭容腔中，液体由于受压而产生压力（其程度由体积弹性模量、总容积等制约）的原理，实际上是液压传动技术的基础。显而易见，封闭容腔中如果只是充满液体，而无外界的作用力，其中的液体除了受一般略去不计的重力之外，是不会产生压力的。正是由于在封闭容腔中的液体受（外部）作用力，而且常伴随不应忽略的体积有所减小，才产生压力（这里应该有两层意思：首先油液要将执行机构的几何容腔V充满；其次，要补充由于液体压缩而减小的那部分体积）。这种情况在液压传动系统中也是一个基本现象。例如：工作液体在充满执行机构（如液压缸）的工作容腔之前，系统一般建立不起压力，只有工作液体充满执行机构工作容腔，推动执行机构克服外负载时，系统才建立起由外负载所决定的压力（当然系统压力往往由像溢流阀这类压力阀来加以限制）。也正由于这个缘故，有理由将一般封闭容腔的压力公式，在一定条件下拓展应用于液压系统的压力容腔。而在一般的教材和技术书籍中，往往在得出液体的体积弹性模量公式后，总有类似这样的一些话：“液压油的可压缩性对在动态下工作的液压系统来说影响极大；但当液压系统在静态（稳态）下工作时，一般可以不予考虑。”其实这是一种不恰当的说法，其对液压技术工作者来说可能是一种误导。