端尺寸的方法及计算流程

对于圆锥体和锥孔主要是角度和大小端尺寸的检测，在第二章第二节中叙述了圆锥体工件计算方法，这里主要从检测方面对内外锥体计算进行介绍。

1.外锥体角度计算

外锥体角度使用角度尺（图10-21）或角度块进行检测，大批量加工中，可使用角度样板（图10-22）或专用工具进行检测（图10-23）；检测精度要求较高的工件时常使用钢柱法和正弦法进行检测。

（1）钢柱法检测外锥体角度图10-24所示以圆锥体小端面为基准，在平板上测得两钢柱外围尺寸N，再把两钢柱垫高H，测量它的外围尺寸M，通过计算来求出它的圆锥半角β。

图10-21 角度尺结构形式

a）游标万能角度尺 b）游标角度尺

图10-22 角度样板检测外圆锥角度

图10-23 专用工具检测外圆锥角度

在直角三角形ABC中，钢柱中心升高量AB等于垫块高H，钢柱中心水平移动量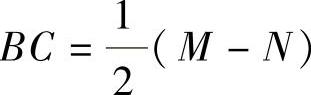，于是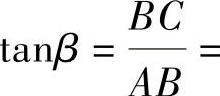

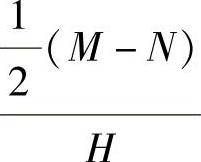
图10-24 钢柱法检测外锥体角度

【例】 一圆锥体测得两钢柱外围尺寸N=49.38mm，垫高H=50mm后测得钢柱外围尺寸M=52.43mm，计算圆锥半角β为多少？

【解】 用式（10-23）计算：

查三角函数表得：β=1°45′。

（2）使用正弦规检测外锥体角度正弦规由一个矩形长方体和两个直径相等的精密圆柱组成（图10-25），它利用正弦函数原理，能够精确地测量圆锥面的角度，是一种间接的测量量具。正弦规的两圆柱中心距L的精度很高，两圆柱中心线与基板工作面间的平行度要求也很高，这样，可保证很小的测量误差。

图10-25 正弦规

图10-26 正弦规测量外锥体

图10-26中，在精密检验平板上，把正弦规的一个钢柱用量块垫上一定高度H，使被测工件放置在正弦规上面以后，上母线和平板平行，再用千分表来测量上母线两端是否等高，以便确定工件锥度是否符合要求。垫高H的大小是根据工件圆锥角α大小来计算的，在直角三角形ABC中，sinα=BC/AB=H/L，于是：

H=Lsinα （10-25）

式中 H——正弦规垫高量块尺寸（mm）；

L——正弦规两圆柱间中心距（mm），L一般为100mm和200mm。

式（10-25）中的H还可用下面方法计算：

式中 C——被测外锥体工件的锥度（°）；

L——正弦规两圆柱间中心距（mm）。

实际工作中，正弦规所垫量块一般不超过5块，这是为了尽量减少测量误差，因为千分表在工件两端测量时所得值总不可能完全相同，总会出现误差值。所垫量块如果少垫了，这就相当于降低了工件小端，而出现图10-27a所示情况，而使测得的角度值增大；如果量块多垫了，就相当于降低了工件的大端，而出现图10-27b所示的情况，而使测得的角度值变小，本来锥角等于基本值的工件，测出的圆锥角α却小于基本值。所测圆锥角锥度误差Δ_θ用式（10-27）计算：

Δ_h=lsinΔ_θ （10-27）

式中 l——千分表在两点测量的长度（mm）；

Δ_h——千分表在两个测量点读数差（mm）；

Δ_θ——工件圆锥角锥度误差。

图10-27 正弦规测量外锥度出现的误差

a）测得角度值增大 b）测得角度值变小

【例】 正弦规两钢柱间的中心距L=100mm，千分表的测量长度l=300mm，被测量圆锥体的圆锥角α=5°25′±10′，问应垫的量块高度H为多少？

【解】 1）用式（10-25）计算H：

H=Lsinα=100sin5°25′=100×0.0944mm=9.44mm

2）用式（10-27）计算Δ_h：(www.xing528.com)

Δ_h=lsinΔ_θ=±30sin10′=±30×0.00291mm=±0.087mm

Δ_h的正负号表示大端比小端高0.087mm或比小端低0.087mm均可。

测量一般用途的锥体时，正弦规应垫量块尺寸见表10-1。

表10-1 测量一般用途锥体，正弦规应垫量块高度

2.外锥体小端直径计算

锥体两端往往做成倒角形式，加上锥体直径又是在斜面上进行测量，所以测出的误差较大。图10-28所示是使用两个钢柱测量外锥体工件小端直径的情况，将工件放在平板上，选择两个相同直径的钢柱，放在工件的外侧，然后用千分尺量出两钢柱外侧最大尺寸L，看它是否符合要求。L为测定值，可用式（10-29）算出：

式中 d——图样中对外锥体小端直径所要求尺寸（mm）；

α——外锥体圆锥半角（°）；

R——钢柱半径（mm）。

由于锥度K=2tanα，式（10-29）可改写成下面的形式：

图10-28 锥体小端直径测量计算

例如，检验锥度为1∶20（等于0.05）的锥体基面尺寸时，如果已知小端直径是20mm，所用的钢柱直径是6.2mm（R=3.1mm），计算两钢柱外侧尺寸L。

图样中大多数是将锥度标注出的，所以利用式（10-31）计算比式（10-29）方便。

实际计算中，最简单方便的是利用查表的方法，即令式（10-31）中的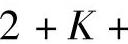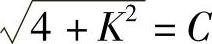，以C作为常数代入（10-31）中，这时：

L=d+CR （10-32）

常数C见表10-2。

表10-2 计算外锥体工件小端直径常数表

（续）

【例】 外锥体工件的锥度为1∶16，图样中所要求小端直径d为19.409mm，所用钢柱半径R=3.1mm（直径为6.2mm），采用图10-28所示两钢柱测量法，问L应是多少？

【解】 从表10-2中查出，常数C=4.0635利用式（10-32）进行计算：

L=d+CR=（19.409+4.0635×3.1）mm=32.006mm

3.计算外锥体大端直径

图10-29a中，在工件的基面A上放置两个直径d相等的小钢圆柱，测出尺寸L的数值。然后，在工件基面上放置两个高度为h的等高量块，再把两个测量小钢圆柱分别放在量块上（图10-29b），再测出尺寸L₁的数值。

图10-29 测量计算外锥体大端直径

a）测出尺寸L b）测出尺寸L1

图10-30所示是两次测量中圆柱的位置及其与工件的相互关系。在直角三角形OO₁A中：

只要知道L、α和d的数值，利用下式可求出大端直径D。

式中 L——第一次测得两钢柱外侧间最大距离（mm）；

α——外锥体半锥角（°）；

d——钢柱直径（mm）。

测量两钢柱外侧最大距离时，要保证两钢柱与工件外锥面接触好，稳住两圆柱，防止其滑动。一般性测量可使用千分尺，比较精密的测量，需在万能测长仪上进行。

图10-30 检测外锥体大端直径计算图