尺寸链的计算方法与应用

1.尺寸链概念

图8-6中，工件是套筒，属于小批生产，采用试切法加工。工件装夹在车床的三爪自定心卡盘中，加工端面2和3。端面1已加工好了。加工端面3时，以端面1做度量基面，保证尺寸A₁。加工端面2时，以端面2做度量基面，保证尺寸A₂。当尺寸A₁和A₂被加工出来后，尺寸A_Δ就随着确定了。显然，尺寸A_Δ的精度取决于尺寸A₁和A₂的加工精度。这样一组尺寸，它们互相关联，构成一个完整的封闭形，它们中间任何一个尺寸有变化，就会引起其他尺寸的变化。这种尺寸关系就叫做尺寸链。

图8-6 尺寸链概念（一）

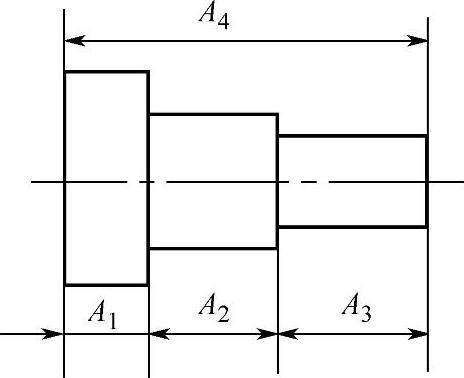
图8-7 尺寸链概念（二）

图8-7所示的阶梯轴，由三段不同直径的外圆组成，每段的长度分别为A₁、A₂、A3总长为A₄。这四个尺寸也构成一个完整的封闭形，所以也是一个尺寸链。在绘制工件图样时，是不允许把尺寸标注成这种封闭的尺寸链的形式，因为在加工时，只需要它们中间任意三个尺寸，就能把三个阶梯的长度按照要求加工出来。但是这四个尺寸所代表的长度都是具体存在的。例如，根据A₁、A₂、A₃三个尺寸把这个阶梯轴加工出来（这里不考虑各个直径的加工问题），加工完了以后，总长尺寸A₄就自然地形成了；也可以根据A₁、A₂、A₄三个尺寸把这个阶梯轴加工出来，加工完了以后，尺寸A₃就自然地形成了。同样，还可以让尺寸A₂或A₁最后自然地形成。

由此可见，尺寸链中的尺寸，有两种不同的类型：一种是加工时直接保证的尺寸，另一种是加工后间接形成的尺寸。

2.组成环和封闭环

为了应用时方便，就把尺寸链中的各个尺寸都叫做“环”。加工时直接保证的尺寸叫做“组成环”，加工后间接形成的尺寸叫做“封闭环”。因为是它使尺寸链封闭起来的。一个尺寸链只有一个封闭环，而组成环可以有两个或更多。

如果把构成尺寸链的这些尺寸画成一个专门的图，这个图叫做尺寸链简图。图8-7所示的阶梯轴的尺寸链简图如图8-8所示。

图8-8 尺寸链简图

根据尺寸链简图，可绕此尺寸链的封闭轮廓，依次把各个尺寸写下来，并标上正负号，当改变方向时就改变符号。这样便可列出尺寸链方程式。

图8-8所示尺寸链的方程式如图8-9所示，从A₁开始向右写，A₂、A₃都和A₁同方向，都标上正号；写到A₄时，就是向左回行了，方向与前面的相反，所以应该标上负号。于是得到如下的尺寸链方程式：

A₁+A₂+A₃-A₄=0

图8-10所示的尺寸链方程式为：

图8-9 尺寸链方程式（一）

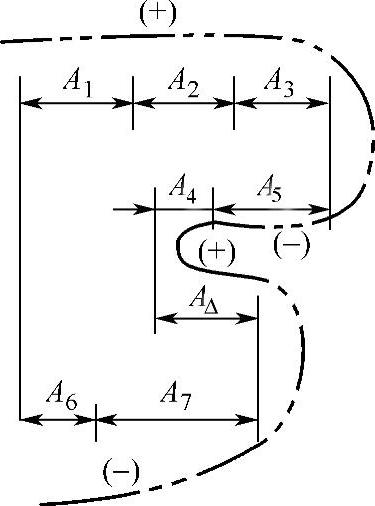
图8-10 尺寸链方程式（二）

A₁+A₂+A₃-A₅-A₄+A_Δ-A₇-A₆=0

尺寸链方程式充分表达了各个组成环和封闭环之间的尺寸关系，学习尺寸链的目的，就是要掌握尺寸链中封闭环与组成环的基本尺寸、极限尺寸以及公差之间的关系。

基本尺寸可以很容易地根据尺寸链方程式计算出来。

如图8-8所示，假定在加工时就直接保证A₁、A₂和A₄，则A₃是加工后自然形成的，是封闭环。设A₄=50mm、A₁=10mm、A₂=20mm，那么封闭环A₃就可求出：

A₃=A₄-A₁-A₂=50mm-10mm-20mm=20mm

由此可以得到一个结论：封闭环的基本尺寸等于各个组成环的基本尺寸的代数和。把这个结论写成一般的公式：

A_Δ=（A₁+A₂+A₃+…+A_m）-（A_m+1+A_m+2+A_m+3+…+A_n-1） （8-1）

式中 A_Δ——封闭环的基本尺寸（mm）；

m——尺寸链中带正号的环的数目；

n——尺寸链中总环数。

上式第一个括弧中的组成环，有一个共同的特点，就是它们的数值如果增大，那么封闭环的数值也随着增大，所以把这些组成环叫做“增环”，也就是说A₁、A2、A3…A_m都是增环。

第二个括弧中的组成环，也有一个共同的特点，就是它们的数值如果增大，那么封闭环的数值便跟着减小。因为括弧的前面是负号。所以把这些组成环叫做“减环”。也就是说：A_m+1、A_m+2、A_m+3…A_n-1都是减环。

当各个增环都是最大极限尺寸，而各个减环都是最小极限尺寸时，就得到封闭环的最大极限尺寸。即：

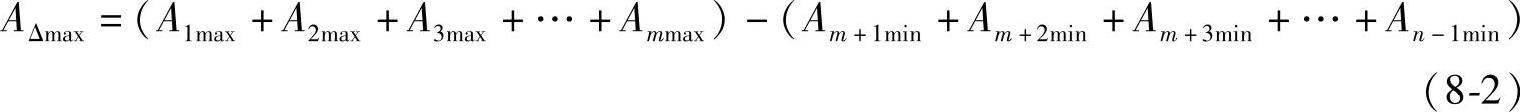
式中，max表示最大值，min表示最小值。

当各个增环都是最小极限尺寸，而各个减环都是最大极限尺寸时，就得到封闭环的最小极限尺寸。即：

根据“公差与配合”可知道，最大极限尺寸等于基本尺寸加上偏差，最小极限尺寸等于基本尺寸加下偏差。用式子写出来就是：

A_max=A+ES，A_min=A+EI。

式中 ES——上偏差；

EI——下偏差。

因此式（8-2）可写成下面的形式：

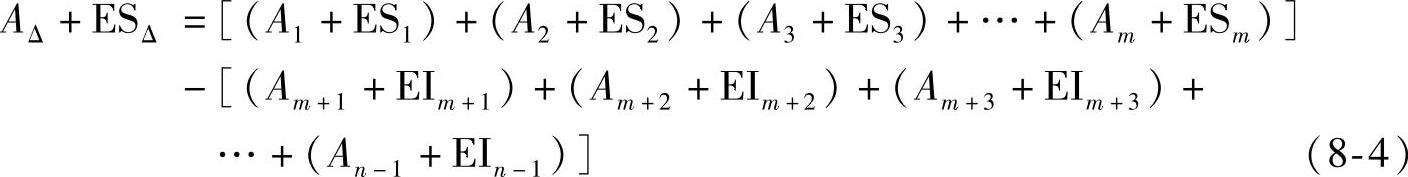
式（8-3）可写成下面的形式：

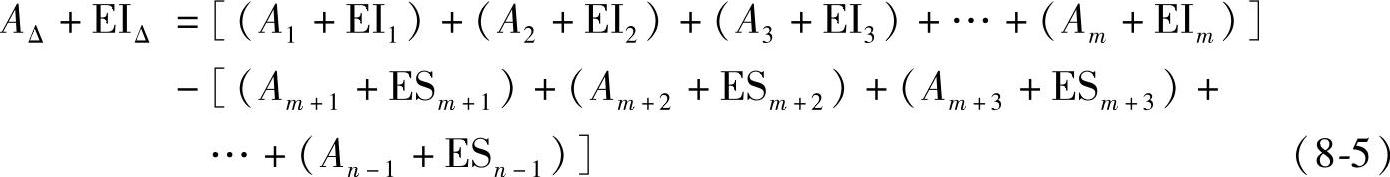
用式（8-4）减去式（8-1），得到：

用式（8-5）减去式（8-1），得到：

于是得到第二个结论：封闭环的上偏差等于所有增环的上偏差之和减去所有减环的下偏差之和；封闭环的下偏差等于所有增环的下偏差之和减去所有减环的上偏差之和。

用式（8-2）减去式（8-3）就得到：

A_Δmax-A_Δmin=（A1_max-A_1min）+（A_2max-A_2min）

+（A_3max-A_3min）+…+（A_n-1max-A_n-1min）令各环的公差分别为δ_Δ、δ₁、δ₂、δ₃…δ_n-1，那么：

将这些数值代入上面的式子中，就得到：

δ_Δ=δ₁+δ₂+δ₃+…+δ_n-1 （8-8）

从这里，可得到第三个结论：封闭环的公差等于各个组成环的公差之和。

把式（8-2）和式（8-3）相加，再用2来除，得到：

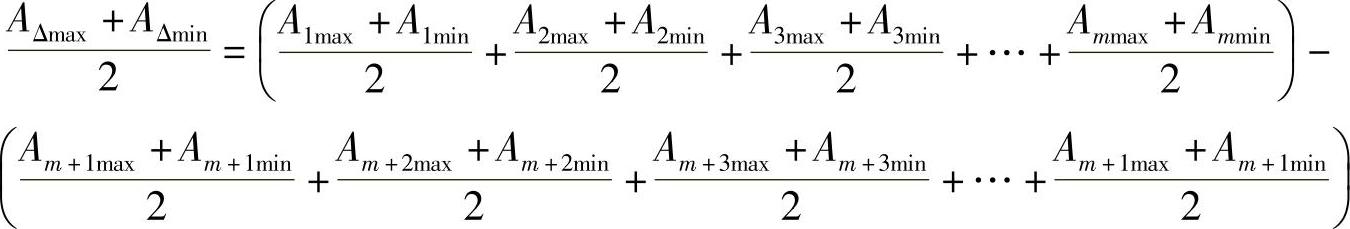
因为任何一个环的最大极限尺寸加上最小极限尺寸，再用2来除，就得到这个环的平均尺寸，所以上面式子中的每一项都代表一个平均尺寸。令A′_Δ、A′₁、A₂′、A′₃…A′_n-1分别表示各个环的平均尺寸，那么上面的式子就变得很简单了。即：

A_Δ′=（A₁′+A₂′+A₃′…+A_m′）-（A′_m+1+A′_m+2+A′_m+3+…+A′_n-1） （8-9）

于是得到第四个结论：封闭环的平均尺寸等于各个组成环的平均尺寸的代数和。

式（8-1）～式（8-9）是用来计算尺寸链的基本公式。

如果某个环的上偏差和下偏差的绝对值相等，例如（20±0.01）mm，（160±0.04）mm，这时，这个环的公差带对称于基本尺寸，所以它的平均尺寸和基本尺寸是相同的。如果某个环的上偏差和下偏差的绝对值不相等，例如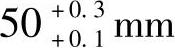、，就要把它的平均尺寸求出来，把它的公差带变成对称于基本尺寸（平均尺寸）的形式，然后才能应用式（8-9）来计算有关的尺寸链问题。因所以由已知环的基本尺寸和上、下偏差，求平衡尺寸时，就可用这个公式，即：

式中 A′——平均尺寸；

A——基本尺寸；

ES——上偏差；

EI——下偏差。

例如：

式中 δ——公差。(www.xing528.com)

上面介绍的这些计算内容，就是关于尺寸链的基本理论。上面的公式，操作者应该真正弄清楚它的意思，的确，这些烦琐的数字公式不易理解，更不好记忆，若把这些公式改写成下面的样子，就便于记忆了。

封闭环公称尺寸=（增环基本尺寸之和）-（减环基本尺寸之和）

封闭环最大极限尺寸=（增环最大极限尺寸之和）-（减环最小极限尺寸之和）

封闭环最小极限尺寸=（增环最小极限尺寸之和）-（减环最大极限尺寸之和）

封闭环的上偏差=（增环的上偏差之和）-（减环的下偏差之和）

封闭环的下偏差=（增环的下偏差之和）-（减环的上偏差之和）

封闭环的公差=组成环的公差之和

封闭环平均尺寸=（增环平均尺寸之和）-（减环平均尺寸之和）

3.尺寸链计算示例

下面举例说明计算尺寸链的方法。

【例1】 已知一尺寸链如图8-11所示，求封闭环的基本尺寸A_Δ和它的公差δ_Δ。

【解】 有三种计算方法。

【方法1】 用式（8-1）～式（8-3）计算。

第一步，由式（8-1）求封闭环的基本尺寸：

图8-11 尺寸链计算示例一

A_Δ=（90+50-24-40-75）mm=1mm

第二步，用式（8-2）、式（8-3）求封闭环的最大极限尺寸与最小极限尺寸：

A_Δmax=（90.8+50-23.7-39.7-74.8）mm=2.6mm

A_Δmin=（90+49.5-23.9-40-75.2）mm=0.4mm

第三步，求封闭环的公差：

δ_Δ=A_Δmax+A_Δmin=（2.6-0.4）mm=2.2mm

由于最大极限尺寸减其基本尺寸所得的代数差称为上偏差ꎻ最小极限尺寸减其基本尺寸所得的代数差称为下偏差，所以所求的封闭环为。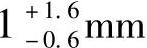

【方法2】 用式（8-1）～式（8-7）计算。

第一步，同方法1。

第二步，由式（8-6）、式（8-7）求封闭环的上偏差与下偏差：ES_Δ=（0.8+0）mm-[（-0.2）+（-0.3）+（-0.3）]mm=（0.8+0.8）mm=1.6mm EI_Δ=[0+（-0.5）]mm-[0.2+0+（-0.1）]mm=（-0.5-0.1）mm=-0.6mm

第三步，求封闭环的公差：

δ_Δ=ES_Δ-EI_Δ=[1.6-（-0.6）]mm=（1.6+0.6）mm=2.2mm

实际上，在第二步做完后就已经求出了这个封闭环的数值，即。

【方法3】 用式（8-1）～式（8-10）计算。

第一步，同方法1。

第二步，由式（8-10）求各组成环的平均尺寸：

（75±0.2）mm不用计算。

第三步，由式（8-9）求各组成环的平均尺寸：A_Δ′=（90.4+49.75-23.8-39.85-75）mm=1.5mm

第四步，由式（8-8）求封闭环的公差：

δ_Δ=（0.8+0.5+0.2+0.3+0.4）mm=2.2mm

所以，封闭环是（1.5±1.1）mm或1⁺_-01..66mm。

【例2】 图8-12所示的尺寸链，封闭环为mm，试求组成环A₁。

图8-12 尺寸链计算示例二

【解】 用【方法2】计算。

尺寸链方程式为：45mm+35mm-60mm+A₁+50mm-100mm=0，所以

A₁=（100+60-45-35-50）mm=30mm

要迅速识别哪些是增环，哪些是减环，把尺寸链方程式整理成式（8-1）的样子：

50=（100+60）-（45+35+A₁）所以、是增环，（45±0.2）mm、、A₁是减环。

用式（8-6）、式（8-7）求A₁₀的上偏差ES₁与下偏差ΕΙ₁：

1.4mm=（0.7+0.4）mm-（-0.2mm+0.1mm+EI₁）

EI₁=（0.7+0.4-1.4+0.2-0.1）mm=-0.2mm

-0.6mm=（-0.1+0）mm-（0.2mm+0.3mm+ES₁）

ES₁=0.6-0.1-0.2-0.3mm=0因此所求的组成环是。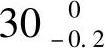

由上面的例题看来，计算尺寸链的工作是不困难的，但必须细心，以免发生错误。进行尺寸链计算时，有两点必须注意：

1）在计算基本尺寸和平均尺寸时，不要弄错了各个环的正负号。要严格按照写尺寸链方程式的规则进行。像例1中的尺寸链，只有两排尺寸，比较简单。上排尺寸为正，下排尺寸就是负。上排尺寸为正，下排尺寸就是负。或者把上排尺寸写在等号的左边，把下排尺寸写在等号的右边。这时出差错的可能性是比较小的。

当尺寸链比较复杂时，它有四排（图8-12）或更多排的尺寸，那就要特别注意各个环的正负号了。

2）在求平均尺寸时，要计算，在求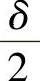时，又要计算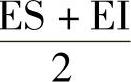。这时很容易混淆，要特别注意。

至于究竟采用哪一种计算方法好，要看具体情况而定。方法1的特点是直接求出最大极限尺寸与最小极限尺寸，但标注尺寸时需要的是基本尺寸和上、下偏差，所以还要拐个弯。而方法2却能直接求出上偏差与下偏差。所以一般情况下，用方法2计算比较简便。当需要知道极限尺寸时，例如查明加工余量的极限值，就应该采用方法1。

如果尺寸链各个环的公差带对称于基本尺寸，各环的基本尺寸就是平均尺寸，这时用方法3计算最为简便。虽然任何尺寸都可以用式（8-10）把它的公差带化成对称于平均尺寸的形式，但计算工作量较多，不熟悉时容易出差错。计算熟练了，只需心算就可以很快把平均尺寸写出来，根本用不着照式（8-10）去套，那时就可能喜欢用方法3了。

为了熟练掌握尺寸链的计算方法，读者必须把式（8-1）～式（8-10）的意思彻底弄明白，牢牢记住。只有这样，才会熟能生巧。

4.尺寸链计算在加工中的应用

机械加工工艺过程的安排，可以用尺寸链方面的道理来指导，图8-13所示轴件，如果它属于小批生产，可在普通车床上用试切法加工。图样上的这些尺寸表示这个阶梯轴各部分长度。端面4至端面5的这段长度，没有标注尺寸，它就是这个尺寸链的封闭环。

实际加工中，如果安排的工艺过程，与图样中的尺寸注法相协调，也就是说，凡是图样上标注的尺寸，在加工时都是直接保证的，那么加工后自然形成的尺寸恰好就是图样上尺寸链的封闭环。这样，在按每个尺寸加工时，就可做到“公差用足”，因而是最经济合理的。这时，图样中的尺寸链和工艺过程中的尺寸链是相同的。所以在加工这个轴件时，应该直接保证图样中所标注的各个尺寸。

图8-13 轴件加工图

假如在加工过程中，不遵守这个原则，而是硬要把图样中尺寸链的封闭环先加工出来，例如直接保证尺寸、（30±0.1）mm、（40±0.15）mm以及端面4至端面5的距离尺寸A，最后自然地形成端面2至端面3的距离尺寸50^+δ0x mm，那么工艺过程中的尺寸链就是图8-14所示的样子，这里的封闭环是尺寸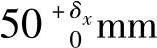。根据尺寸链关系，封闭环的公差等于各个组成环的公差之和。用式子表示就是：

δ_x=0.6+0.2+0.3+δA

组成环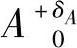的基本尺寸A很容易计算出来，公差δ_A可以根据经济的加工精度规定一个适当的数值。但是δ_x的数值不能大于0.2mm，这是图样中的设计要求。为了保证这个要求，做到δ_x=0.2mm，有什么办法呢？唯一的办法只有压缩各个组成环的公差。这就增加了加工的难度，使生产率降低，废品率增加，这是加工时所不希望的。

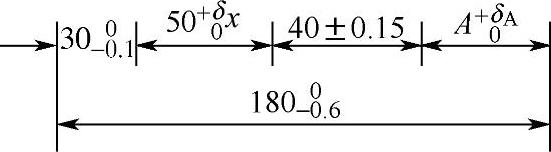
图8-14 尺寸链出现的一种形式

所以应该力求按照图样上的尺寸注法安排工艺过程，使图样中尺寸链的封闭环在加工中最后自然地形成，以做到“公差用足”。