应用几何定理求算尺寸的常用方法

利用几何方法求算长度，勾股定理用得最多。应用勾股定理进行计算，也需要先组成一个直角三角形，其计算和用三角函数中的方法大致相同。

1，应用几何计算组成直角三角形

图1-15所示是个截圆形，已知直径d和平面间厚度h，求平面部分的宽度b，这时，从A点到B点和A点到C点作辅助线，这样，d、b和h组成了直角三角形ABC。

图1-16中，已知R和H，求算L，这时，利用简算后的已知数（R-H）和R及要求算的数L组成直角三角形ABC，进行计算。

图1-15 截圆形（一）

图1-16 带圆角工件

图1-17中，已知弓形长S和弓形半径R，求算弓形高b，这时，可利用未知数h和已知数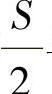与R组成直角三角形ABO，求出h，则可算出b（b=R-h）。

2，应用几何定理计算示例

（1）截圆形尺寸互算图1-18所示是截圆形，D是圆的直径，A是平面部分的宽度，B是两平面对边距离。计算长度和距离时，根据勾股定理得到下式：

图1-17 弓形工件

图1-18 截圆形（二）

公式简化后得：D²=A²+B2

于是

【例】 有一工件直径D=30mm（图1-19），平面部分的宽度A要求为22mm，问对边距离B是多少？

【解】 用式（1-3）进行计算：

（2）凹圆弧尺寸互算在图1-20中，圆弧半径为R，圆弧高度是H，圆弧部分长度是L。在阴影直角三角形中，根据勾股定理可得：R²=L²+（R-H）2，即R²=L²+R²-2RH+H²，则：

2RH=L²+H² （1-4a）

图1-19 方截圆形

由式（1-4a）得：

又由式（1-4a）得：H²-2RH+L²=0，解二次方程式得：

所以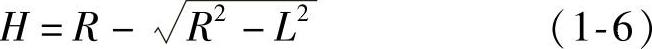

【例】 设工件（图1-20）槽深H=10mm，要在长15mm内用圆弧来连接，问圆弧半径R为多少？

【解】 用式（1-4b）进行计算：

（3）轴圆角尺寸互算图1-21所示的轴件，大直径D和小直径d，用圆角半径R连接，圆弧段的轴向长度L，它们的互算方法实际上和图1-20所示的圆角工件是一致的，这时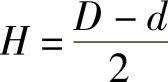，，代入式（1-4b）和式（1-5）后得：

图1-20 带凹圆弧工件

【例】 图1-21的圆轴，大直径D=35mm，小直径d=25mm，在大小两轴间的8mm长度内以圆弧连接（即L=8mm），求圆角半径R为多少？

【解】 用式（1-7）进行计算：

【例】 某工件的大小圆轴间的圆弧半径R=8mm，大轴直径D=40mm，小轴直径d=32mm，问圆弧部分的轴向长度L为多少？

【解】 用式（1-8）进行计算：

（4）正三角形和它的内切圆外接圆尺寸互算在图1-22中，正三角形边长S，内切圆直径d，外接圆直径D。在直角三角形OAB中，因∠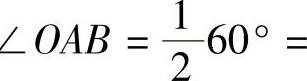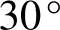，∠BOA=60°，同样根据30°和60°直角三角形定理（图1-9）得：

图1-21 带圆弧半径的轴件

图1-22 正三角形和它的内切圆外接圆

即：

因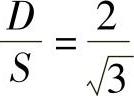，所以：(www.xing528.com)

因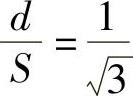，所以：

【例】要加工一个正三角形冲模的冲头，三角形边长是30mm，如果用圆形工具钢来加工，问该用多大直径的圆料？

【解】用式（1-10）进行计算：

D=1，1547S=1，1547×30mm=35mm

（5）孔距的计算如图1-23所示，两个孔中心横向距离是a，纵向距离是b，两孔中心斜距离为c，计算两孔中心距时的公式可利用勾股定理，即：

c²=a²+b² （1-14）

图1-23 两孔距离尺寸

图1-24中的三孔距离尺寸，同样可用以上三个公式来计算。

图1-24 三孔距离尺寸

【例】 图1-23中的两孔距离c=80mm，横向距离a=50mm，求算纵向距离b为多少？

【解】 用式（1-17）进行计算：

如图1-25所示，需要知道多孔工件中心距时，使用游标卡尺量出壁厚和相邻两孔的直径，然后用公式计算。图中，大孔直径为D，小孔直径为d，壁厚为N，两孔中心距用式（1-18）计算：

式中 A——相邻两孔中心距（mm）。

对于不便于测量或数值要求很精确时，两孔中心距可利用勾股定理计算。

图1-25 孔心距及其计算

a）两孔工件 b）三孔工件

从图1-25a可知：

所以A=M+O₁′B+O₂′C

式中 A——两孔中心距（mm）；

M——千分尺测量两孔壁间厚度（mm）；

D——大孔直径（mm）；

d——小孔直径（mm）；

L——千分尺测量触头直径（mm）。

（6）圆锥体垂直高和斜高互算图1-26所示是个圆锥体，垂直高h，斜高l，底圆直径D，在阴影直角三角形中，根据勾股定理可得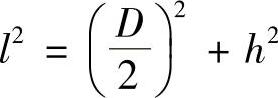：，于是：

【例】 一圆锥体底圆直径D=100mm，垂直高h=140mm，问斜高l为多少？

【解】 用式（1-20）进行计算：

（7）截圆锥体垂直高和斜高互算在图1-27的截圆锥体中，上底直径为d，下底直径为D，垂直高h，斜高l，在阴影直角三角形中，根据勾股定理可得：

图1-26 圆锥体

图1-27 截圆锥体

于是

【例】 一截圆锥体上底直径d=200mm，下底直径D=320mm，垂直高h=210mm，求算它的斜高l为多少？

【解】 用式（1-22）进行计算：