应力积分法的使用及优化

应力积分法可用于连续有限元模型所得应力的线性化。对于二维或三维有限元连续单元分析的结果，沿应力分类线通过壁厚对应力分量进行积分确定薄膜和弯曲应力，峰值应力则由总应力减去薄膜和弯曲应力得到。对于二维和三维有限元壳体单元，则可由分析结果直接导出薄膜应力、弯曲应力和峰值应力。

1．连续单元的应力线性化

采用二维或三维实体连续单元进行有限元分析，所得的应力结果可以采用应力积分法进行线性化处理。沿应力分类线通过壁厚对应力分量进行积分，以确定薄膜和弯曲应力分量。用总应力分布扣除薄膜和弯曲应力分布来直接得到峰值应力分量，此时用于计算应力分量的坐标系为应力分类线定位所在的局部坐标系，如图5.6所示。

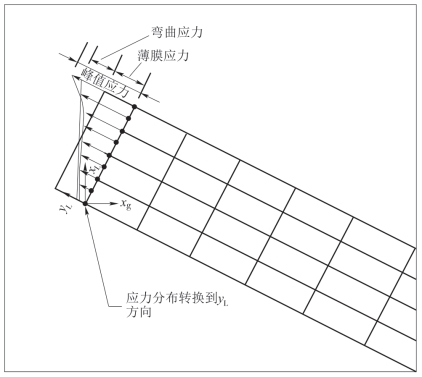
图5.6　有限元所得总应力的线性化

第1步：计算薄膜应力张量。

薄膜应力张量是由沿应力分类线的各应力分量的平均值组成的张量，表达式为：

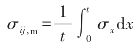
第2步：计算弯曲应力张量。

仅对局部环向和经向（正）应力分量计算弯曲应力，并不对平行于应力分类线的局部应力分量或面内剪切应力计算弯曲应力。

当剪切应力分布引起应力分类线扭转时，剪切应力的线性部分需要考虑。例如环向-法向平面中的面外剪切应力。

弯曲应力分量由沿应力分类线的各应力分量的线性变化部分所组成：

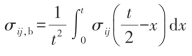
第3步：计算峰值应力张量。

峰值应力张量的分量等于下式的张量：(www.xing528.com)

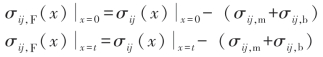
第4步：计算主应力。

以薄膜应力和薄膜应力加弯曲应力分量为基础，计算在应力分类线端部的3个主应力。

第5步：计算当量应力。

以薄膜加弯曲应力分量为基础，用下式计算应力分类线端部的当量应力：

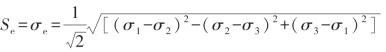
2．壳体单元的应力线性化

采用二维或三维壳单元进行有限元分析，所需的应力结果可以直接由分析结果得出。根据由式计算的当量应力，导出应力分布中的薄膜应力张量、弯曲应力张量和峰值应力张量。

第1步：导出薄膜应力张量。

由沿应力分类线各应力分量的平均值组成。

第2步：导出弯曲应力张量。

由沿应力分类线各应力分量的线性变化部分组成。

第3步：导出峰值应力张量。