不连续应力（边缘应力）的分析方法

1．不连续应力

采用板壳理论求解总体结构不连续的总应力，如图2.1所示。

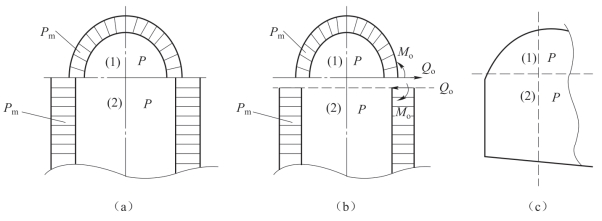
图2.1　连接边缘处的变形协调

由于圆筒和封头的母线曲率不同，所以无法由无力矩理论所得的圆筒和球壳应力公式直接求解连接处的总应力，只能用和一般超静定结构分析相类似的方法求解。先将圆筒和半球形封头的连接分离为单个的圆筒和球壳，分别按圆筒、球壳的无力矩应力公式求出各自的应力，这样求出的应力在包括连接边缘处在内的整个圆筒和整个封头上必然是不同的。设圆筒上的应力为，封头上的应力为，也就是在连接边缘处引起不同的变形而导致两元件“分离”，即变形不协调，如图2.1（a）所示。为保持两个元件在连接处实际上的变形协调，即恢复结构的连续性，一般两个元件的连接边缘处必然有大小相等、方向相反，属于自平衡力系的超静定力矩和剪力，或称边缘力矩Mo和边缘剪力Qo存在，如图2.1（b）所示。此两元件上的边缘力矩和边缘剪力使两元件在连接处产生各自的应力和，即边缘应力，包括薄膜应力和弯曲应力。在应力分类中，分别划分为局部一次薄膜应力类和二次应力类，如图2.2所示，使两元件产生各自的向内和向外的变形，从而消除了变形不协调量，如图2.1（c）所示。

不论是圆筒还是封头，它们连接处附近的总应力不仅包括由压力直接引起的应力，还包括为使连接处保持变形协调所引起的边缘应力。

圆筒上的总应力为：

封头上的总应力为：

(www.xing528.com)

2．不连续应力自限性

根据引起边缘应力的原因，当压力容器的压力为P1时，由无力矩理论所得圆筒和变形不协调量为Δ1（此变形不协调量也可称为“自由”变形不协调量，即设想为两元件相互不受约束时的变形不协调量），相应地，为消除此不协调量而存在的边缘力矩和边缘剪力分别为Mo1和Qo1，如图2.2（a）所示。

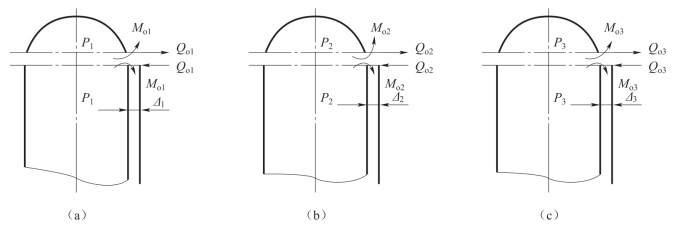
图2.2　边缘应力的自限分析

当压力容器压力增加到P2时，圆筒和封头的变形不协调量相应增加到Δ2，相应地，为消除此不协调量而存在的边缘力矩和边缘剪力分别为Mo2和Qo2，如图2.2（b）所示。当压力容器压力增加到P3时，圆筒和封头的变形不协调量相应增加到Δ3，相应地，为消除此不协调量而存在的边缘力矩和边缘剪力分别为Mo3和Qo3，如图2.2（c）所示。设想当边缘力矩和边缘剪力尚未达到Mo3和Qo3，并且尚未全消除Δ3时，两元件中的任一者因附加边缘应力的作用而使其总应力达到材料的屈服强度而屈服，并假定材料为理想塑性材料，则由于已屈服元件在不增加应力的情况下变形可以任意增加，导致其中任一元件的屈服，从而使得在该应力时尚剩余的变形不协调量自动消除，所以，此时不必达到Mo3和Qo3即可消除变形不协调量Δ3。如再增加压力，尽管其变形不协调Δ值还会相应增加，但边缘力矩Mo、边缘剪力Qo，以及相应的边缘应力和总是保持在使其中任一元件达到屈服时的水平，这就是边缘应力具有自限性的原因。

由上可知，其一，边缘应力的自限性是由其导出方法所决定的，它并不是由外载和内力的平衡关系导出的，而是由两个元件间的变形协调关系导出的。一切由温度梯度引起的温差应力，不论是总体的或局部的，都是由变形协调关系导出的，所以都具有自限性。其二，如果用弹性力学方法或有限元方法求解圆筒和封头连接的边缘问题，则由于它和由板壳理论求解边缘问题的方法完全不同，它并不需要将连接的两元件先行分离，而是把两元件的连接处看作一个结构，直接求得其总应力。所以，如果按有限元方法得到总应力，则要按照以板壳理论方法所建立的应力分类原理进行分类，这就存在如何按板壳理论求解过程进行分解半正确分类的不相匹配问题。

3．不连续应力衰减性

由边缘力矩Mo、边缘剪力Qo在圆筒或封头上引起的边缘应力可以由图2.3所示的模型求得。它在两元件上都可以引起周向和径向的薄膜和弯曲应力。它们都随离连接处的径线方向位置而衰减，一般来说，在离连接处的经线距离处，即可衰减至工程上可以忽略不计的程度。所以，在规范中经常用来表示应力集中存在的范围。开孔补强时，在壳体上的补强有效范围用表示，在接管上的补强有效范围也用表示。

图2.3　边缘应力的求解