时序逻辑电路分析技巧总结

时序逻辑电路的特点是：任一时刻的输出不仅取决于该时刻电路的输入变量，而且还与电路原来的状态有关，因此时序逻辑电路必须包含具有记忆功能的存储电路（触发器），并且其输出状态与输入变量一起决定电路的次态。

时序逻辑电路由组合逻辑电路和存储电路相互连接构成，如图10-31所示，为时序逻辑电路结构框图。图10-31中，（x1…xi）为一组输入变量，（y1…yj）为一组输出变量，（p1…ps）为一组存储电路输入变量，（q1…qk）为一组存储电路输出并反馈至组合逻辑电路输入的变量。由图10-31可见（x1…xi）和（q1…qk）共同作用产生（y1…yj）和（p1…ps）。而（p1…ps）又决定了（q1…qk）。

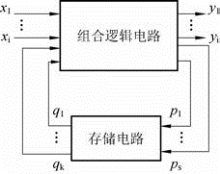
图10-31　时序逻辑电路结构框图

1.时序逻辑电路分类

（1）时序逻辑电路按电路输出信号的特性分为：穆尔型（MOORE）和米莱型（mealy），满足输出方程的为米莱型；若输出只与存储电路现态有关，与现态输入Xtn无关，构成Ytn＝F[Qn]关系，称为穆尔型，这两种电路的分析和设计过程基本上是一致的。

（2）时序逻辑电路按逻辑功能分为计数器、寄存器、移位寄存器、顺序脉冲发生器，以及实现各种不同操作的时序电路。

（3）时序逻辑电路按其工作方式可分为同步时序电路和异步时序电路。

①同步时序电路：电路中各存储单元的更新是在同一时钟信号控制下同时完成。

②异步时序电路：电路中各存储单元无统一的时钟控制，不受同一时钟控制。

2.时序逻辑电路分析方法

1）时序电路描述方法

描述时序电路的逻辑功能可以采取逻辑方程式、状态转换表、状态转换图、时序图（波形图）等方式。

（1）逻辑方程式。

图10-30中，用（x1…xi）代表输入变量，（y1…yj）代表输出变量，（p1…ps）代表存储电路输入驱动变量，（q1…qk）代表存储电路输出状态，这些信号之间的关系可用以下三个逻辑方程表示。

输出方程：

状态方程：Qn＋1＝

驱动方程：

输出方程说明输出信号是输入信号和存储电路输出Qn的函数（米莱型）。

状态方程说明存储电路的次态Qn＋1是其存储输入和现态Qn的函数。

驱动方程说明存储电路输入驱动信号是输入信号和现态Qn的函数。

（2）状态转换表。

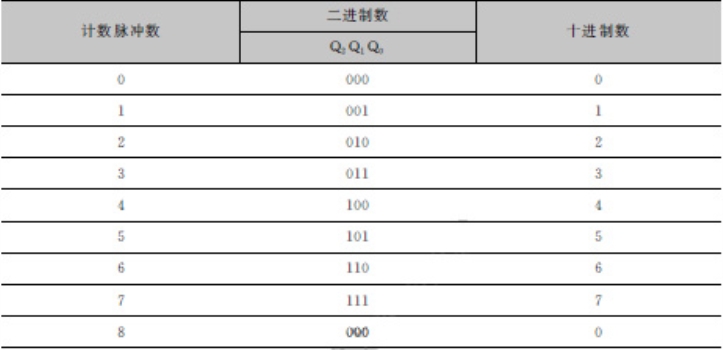
状态转换表又称状态表，它是时序电路输入状态与对应输出状态和存储电路（触发器）现态、次态关系表。如表10-13所示，为3位二进制计数状态转换表。

表10-13　3位二进制计数状态转换表(www.xing528.com)

（3）状态转换图。

状态转换图又称状态图，它以图形方式表示时序电路状态转换的规律，图10-32是两变量状态转换图，Q1Q0由现态转换为次态。

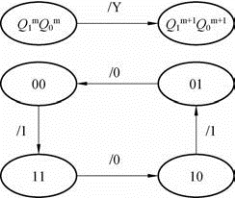
图10-32　状态转换示意图

（4）时序图。

时序图又称波形图，它表示时序电路输入信号、输出信号和电路状态在时间上的对应关系。图10-33为脉冲时序图，输出Y与时钟脉冲CP、现态输出Q1n、Q0n关系。

上述四种分析方法是对时序电路逻辑关系不同描述，适用于任何形式的时序逻辑电路。

2）时序逻辑电路分析步骤

（1）写方程组。

根据给定的逻辑电路图分别写出以下方程组。

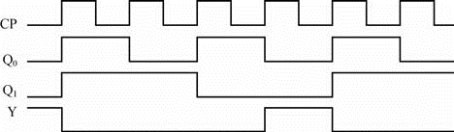
图10-33　时序示意图

①时钟方程组：由存储电路中各触发器时钟信号CP的逻辑表达式构成。

②输出方程组：由时序电路中各输出信号的逻辑表达式构成。

③驱动方程组：由存储电路中各触发器输入信号的逻辑表达式构成。

（2）求状态方程组。

将驱动方程代入各相应触发器的特性方程，得到各触发器的状态方程，即各触发器次态的输出逻辑表达式。

（3）列状态转换表。

依次假定电路现态Qn，代入状态方程组和输出方程组，求出相应的次态Qn＋1和输出，并列表。

（4）画状态转换图。

画状态转换图，可更为直观地反映电路工作特性。

思考题：时序逻辑电路分析中，如何得出状态方程组？