逻辑函数简化技巧

1.逻辑代数化简

根据三种基本逻辑运算，可推导出一些基本公式和定律，形成了一些运算规则，熟悉掌握并且运用这些规则，十分重要。

（1）0-1定律：

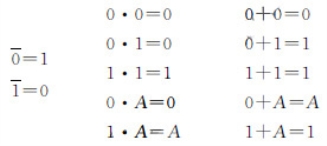
（2）重叠律（自等律）：

A·A＝A，A＋A＝A

（3）互补律：

（4）还原律：

（5）交换律：

A·B＝B·A，A＋B＝B＋A

（6）结合律：

（A·B）·C＝A·（B·C），A＋B＋C＝A＋（B＋C）

（7）分配律：

A·（B＋C）＝AB＋ACA＋BC＝（A＋B）（A＋C）

（8）反演律（德·摩根定理）：

（9）吸收律：

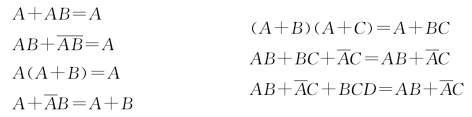
2.卡诺图化简

代数化简法需要熟练地掌握公式，并具有一定的技巧，还需要判断所得到的结果是否是最简式，所以在化简较复杂的逻辑函数时有一定的难度，为解决此问题，人们常用卡诺图化简法化简。

1）逻辑函数的最小项和最小项表达式

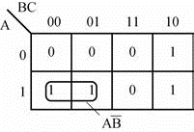
（1）最小项：对于n个变量函数，如果其与或表达式的每个乘积项都包含n个因子，而这n个因子分别为n个变量的原变量或反变量，每个变量在乘积项中仅出现一次，这样的乘积项称为函数的最小项表达式。通常用符号mi来表示最小项，其中把最小项中的原变量记为1，反变量记为0，当变量顺序确定后，可以按顺序排列成一个二进制数，则与这个二进制数相对应的十进制数，就是这个最小项的下标i。图10-6所示为4变量卡诺图。

（2）最小项的性质。

①在所有最小项中，有一个且仅有一个最小项的值为1。

②任意两个最小项的乘积为0。

③全体最小项的和为1。

（3）最小项的几何相邻和逻辑相邻。

①公因子。

在逻辑函数与或表达式中，如两乘积项仅有一个因子不同，而这一个因子又是同一变量的原变量和反变量，则两项可合并为一项，消除其不同的因子，合并后的项为这两项的公因子。如乘积项、AB中出现A的原变量和反变量，则可合并后消去A变量，合并为B。

②逻辑相邻。

最小项组成或项可消去互补因子的性质称为逻辑相邻。如图10-7所示，m4和m5是相邻的，m4即，m5即，这两项中只有变量C不同，这两项合并，即，可见两个逻辑相邻项可以合并成一项，消去那个不同的变量。

③几何相邻。

凡是在图中几何相邻的项，就一定具有逻辑相邻性，如将这些相邻项相加，则可消去多余的因子。如图10-8所示，m5、m7、m13、m15是几何相邻的项，将这些相邻项相加，可消去A、C变量。

图10-6　4变量卡诺图

(www.xing528.com)

图10-7　逻辑相邻项卡诺图

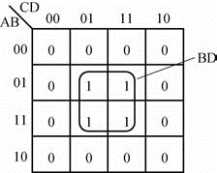
图10-8　几何相邻项卡诺图

2）卡诺图的化简方法

卡诺图是一种矩阵式真值表，比真值表直观了许多。如图10-6，卡诺图中变量取值按照格雷码（循环码）的编码顺序00，01，11，10进行排列。这种码使得相邻两个方格对应的最小项仅有1个变量不同。

（1）卡诺图有如下特点。

①n个变量的卡诺图有2n个方格，每个方格对应一个最小项。

②每个原变量与反变量将卡诺图等分为两部分，并且各占的方格个数相同。

③卡诺图上两个相邻的方格所代表的最小项，只有1个变量不同。

（2）卡诺图的填入。

因为构成函数的每个最小项中，都有一组变量的取值使该最小项为1，所以在构成函数的每个最小项相应的方格中填1，而其他方格填0。

3）卡诺图的化简步骤

（1）首先将逻辑函数变换成与或表达式。

（2）画出逻辑函数的卡诺图。

（3）将2n个为1的相邻方格分别画方格群，整理每个方格群的公因子，作为乘积项。

①圈要尽量大。每个相邻最小项构成的矩形应包含尽可以多的最小项，使得化简后的“与”项包含的变量个数最少

②圈的数量要尽量少。相邻最小项构成的矩形个数尽可能少，使得化简后的“与”项个数最少。

③被圈过的“1”可以重复用。所选择的相邻最小项的矩形应包含所有构成函数的最小项（即卡诺图中为1的方格）并且每个相邻最小项构成的矩形中至少有1个最小项没有被选择过。

④要把所有的“1”都圈完。

（4）将整理后的乘积项加起来，就是化简后的与或式。

例10-4

如图10-9所示，利用卡诺图法化简函数Y＝∑m（3，4，5，6，7，10，11，14，15）。

解

（1）填图；（2）画卡诺圈；（3）合并相邻项。化简结果为：

4）带约束函数的卡诺图化简

因为十进制数码只有0～9，从1010到1111共6个编码没有对应的十进制数，它们属于伪码。所以卡诺图化简填图时，可以填“1”或填“0”。具有约束项的逻辑函数表示方法，如∑d（11，13，15）。

例10-5

化简具有约束条件的逻辑函数：

Y（A，B，C，D）＝∑m（2，6，7，9）＋∑d（8，10，11，13，14）

解

画出函数Y的卡诺图，如图10-10所示，图中打×的小方格表示约束项“1”。

思考题：卡诺图变量取值是如何进行排列的？

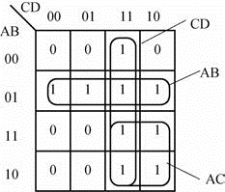
图10-9　例10-4卡诺图

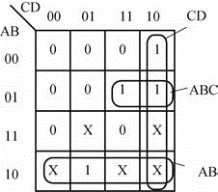
图10-10　例题10-5卡诺图