1.数制
所谓数制就是计数的方法,在生产实践中,人们经常采用位置计数法,即将位置用表示数字的数码按一定的规律排列表示出来。
1)进位制
在表示数时,仅用一位数码往往不够用,必须用进位计数的方法组成多位数码。多位数码从低位到高位的进位规则称为进位计数制,简称进位制。进位制中的基数,就是在该进制中可能用到的数码个数。而位权则表示这一位的权数,权数是一个幂,第i位权数等于该进制基数的i次方。常见的有十进制、二进制、十六进制。
(1)十进制。
十进制数有0,1,2,3,4,5,6,7,8,9等十个符号,计数的基数为10。十进制数的运算加法时遵循“逢十进一”,减法时遵循“借一当十”。十进制数可表示为:

式中:a为0~9中的任一数码,10为进制的基数,第i位的位权为10i,m,n为正整数,n为整数部分的位数,m为小数部分的位数。如:
(209.04)10=2×102+0×101+9×100+0×10-1+4×10-2
(2)二进制。
二进制的数码为0、1,进制的基数为2,第i位的位权为2i,进/借位的规则:逢2进1,借1当2。
对于一个二进制数可表示为:

式中:m、n为正整数,n为整数部分的位数,m为小数部分的位数。
如:
(101.01)2=1×22+0×21+1×20+0×2-1+1×2-2
(3)十六进制。
当二进制数位数较多时,很难记忆,而且书写容易出错,通常将二进制数用十六进制表示。十六进制有0、1、2、3、4、5、6、7、8、9、A.B.C.D.E、F共十六个数码,16为进制的基数,第i位的位权为16i,进/借位的规则:逢16进1,借1当16。
对于一个十六进制数可表示为:
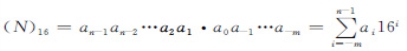
式中:m、n为正整数,n为整数部分的位数,m为小数部分的位数。
如:
(D8.A)16=D×161+8×160+A×16-1=(216.625)10
2)数制之间转换
(1)将十进制转换为二进制时,一般将十进制数的整数和小数分别进行转换。
①十进制整数部分转换采用除基取余法。即除以基数2。先得的余数是所得二进制数的最低位,直至商为0,所得余数为二进制最高位,并按最高位至最低位排列。
如将(17)10转换为二进制数:

②十进制小数部分转换为二进制时,采用乘基取整法。即乘以基数2,先得的乘积整数部分作为最高位。每次乘以2后取出积的整数部分,直至乘积的小数部分为0或达到精度要求为止。按最高位至最低位排列,即为转换的小数部分二进制数。(https://www.xing528.com)
如将(0.3125)10转换为二进制数:

所以(0.3125)10=(0.0101)2。
思考题:十进制小数部分转换成二进制时,先取出的整数是最高位还是最低位?
(2)二进制与十六进制之间转换。
二进制数转换成十六进制数,每4位二进制数为一组转换为对应的十六进制数,整数部分以小数点为分界,由低位向高位,不足4位时高位补0转换;小数部分则从小数点向右,每4位一组,不足4位时低位补0转换。
如:
(1010001.100011)2=01010001.100011002=(51.8C)16
(3)十六进制数转换为二进制数时,一位十六进制数转换为对应的4位二进制数,整数部分以小数点为分界,由低位向高位转换;小数部分则从小数点向右,按位转换。
如:
(7A5.1)16=011110100101.00012
2.码制
1)BCD有权码
BCD(binary coded decimal)是用二进制数表示十进制数的编码。十进制数有1~9共10个数字,对应需用4位二进制码表示,每位二进制码都有相应的位权。同时因十进制只有0~9十个数字,其二进制编码1010~1111这六个代码无意义,称为“伪码”,BCD码与十进制数的对应关系见表10-1和表10-2。
(1)8421BCD码与十进制数的对应。
8421BCD码是有权码,从最高位计算,4位二进制码相应的位权分别为8、4、2、1。
(2)5421BCD码与十进制数的对应。
5421BCD码是有权码,从最高位计算,4位二进制码相应的位权分别为5、4、2、1。
(3)2421BCD码。
2421BCD码是有权码,从最高位计算,4位二进制码相应的位权分别为2、4、2、1。
表10-1 BCD码与十进制数的对应关系1

如将(123)10表示成8421BCD码为(000100100011)8421BCD。
2)BCD无权码
余3码与格雷码都是无权码,余3码比相应的8421BCD码多3(十进制数)。
如:(1000)8421BCD的余3码为(1011)余3码。而格雷码的特点是任意两组二进制相邻代码之间只有一位不同,所以格雷码又称“循环”码。
表10-2 BCD码与十进制数的对应关系2

思考题:为什么说使用十六进制比使用二进制更方便?
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




