正弦稳态电路的分析方法

正弦稳态电路分析

1.元件VCR的相量形式

1）电阻元件VCR的相量形式

设图1-29（a）中流过电阻的电流为：

则电阻电压为：

其相量形式：

（1）电阻电压相量和电流相量满足复数形式的欧姆定律：

（2）电阻电压和电流的有效值也满足欧姆定律：UR＝IR。

（3）电阻的电压和电流同相位，相量图如图1-29（a）所示。

图1-29　元件VCR的相量图

2）电感元件VCR的相量形式

流过电感的电流为：

对应的相量形式分别为：

电感的电压相量和电流相量满足关系：UL＝IXL，其中XL＝ωL＝2πfL，称为感抗，单位为Ω（欧姆），电感电压超前电流相位π/2。如图1-29（b）所示。

3）电容元件VCR的相量形式

设图1-29（c）中电容的电压为：

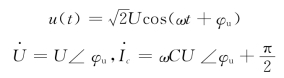
电容的电压相量和电流相量满足关系：

电容电压滞后电流。(www.xing528.com)

2.阻抗和导纳

1）阻抗与导纳

图1-30所示的无源线性一端口网络，当它在角频率为ω的正弦电源激励下处于稳定状态时，端口的电压相量和电流相量的比值定义为该一端口的阻抗Z，单位：Ω。导纳G也为复数，它为复阻抗的倒数。

图1-30　无源线性一端口网络

有：

上式称为复数形式的欧姆定律，其中|Z|＝称为阻抗模，φz＝φu-φi称为阻抗角。由于Z为复数，也称为复阻抗。

2）阻抗（导纳）的串联和并联

若n个阻抗串联的电路，根据KVL得：

式中：Z为等效阻抗。

若n个阻抗并联的电路，同样根据KVL可得：

3.正弦电流电路分析

引入相量法和阻抗的概念后，正弦稳态电路和电阻电路依据的电路定律是相似的，因此，可将电阻电路的分析方法直接推广应用于正弦稳态电路的相量分析中。

例1-3

求图1-31（a）所示电路中的电流。

已知：＝4∠90°A，Z1＝Z2＝-J30Ω，Z3＝30Ω，Z＝45Ω。

解

应用电源等效变换方法得等效电路如图1-31（b）所示，其中：

图1-31　例1-3图

思考题：电感元件其电压超前电流相位π/2，结论对吗？