正弦电路及其研究——求正弦电流的最大值发生时间

正弦电路

1.正弦量

电路中按正弦规律变化的电压或电流统称为正弦量，激励和响应均为正弦量的电路称为正弦电路或交流电路，以电流为例，其瞬时值表达式为（采用cosine函数表示）：

i（t）＝Imcos（ωt＋φ）

波形如图1-25所示。

图1-25　正弦电路波形图

研究正弦电路的意义如下。

（1）正弦函数是周期函数，其加、减、求导、积分运算后仍是同频率的正弦函数。

（2）正弦信号是一种基本信号，任何复杂的周期信号可以分解为按正弦规律变化的分量。

2.正弦量的三要素

（1）Im—幅值（振幅、最大值）：反映正弦量变化过程中所能达到的最大幅度。

（2）ω—角频率：为相位变化的速度，反映正弦量变化快慢。它与周期和频率的关系为：

（3）ψ—初相角：反映正弦量的计时起点，常用角度表示。

3.相位差

相位差是用来描述电路中两个同频正弦量之间相位关系的量。

设：

u（t）＝Umcos（ωt＋φu），it＝Imcos（ωt＋φi）

则相位差为：

φ＝（ωt＋φu）-（ωt＋φi）＝φu-φi

上式表明同频正弦量之间的相位差等于初相之差，通常相位差取主值范围，即：|φ|≤π。

如图1-26（a）所示φ＞0，称u超前i，或i滞u，表明u比i先达到最大值；如图1-26（b）所示φ＜0，称i超前u，或u滞后i，表明i比u先达到最大值；如φ＝0，称i与u同相，如图1-26（c）所示。

图1-26　相位差示意图

需要注意：两个正弦量进行相位比较时，应满足同频率、同函数、同符号时才可比较。

4.正弦电流、电压的有效值

周期性电流、电压的瞬时值随时间而变，为了衡量其平均效应，工程上采用有效值来表示。如图1-27所示，通过比较直流电流I和交流电流i在相同时间T内流经同一电阻R产生的热效应，即令：

从中获得周期电流和与之相等的直流电流I之间的关系：(www.xing528.com)

这个直流量I称为周期量的有效值，有效值也称方均根值。

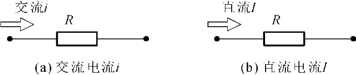
图1-27　直流电流I和交流电流i热效应

设正弦电流：

i（t）＝Imcos（ωt＋φi）

相应的有效值为：

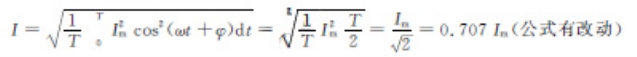
即 正弦电流的有效值与最大值满足关系：

同理，可定义电压有效值：

可得正弦电压有效值与最大值的关系：

若一交流电压有效值为U＝220 V，则其最大值为Um≈311 V。

需要注意以下几点。

（1）工程上说的正弦电压、电流一般指有效值，如设备铭牌额定值、电网的电压等级等。但绝缘水平、耐压值指的是最大值。因此在考虑电器设备的耐压水平时应按最大值考虑。

（2）测量中，交流测量仪表指示的电压、电流读数一般为有效值。

（3）区分电压、电流的瞬时值i、u，最大值Im、Um和有效值I、U的符号。

例1-2

已知正弦电流波形如图1-28所示，ω＝103rad/s。（1）写出正弦i（t）表达式；（2）求正弦电流最大值发生的时间t。

解

根据图1-29所示可知电流的最大值为100 A，t＝0时电流为50 A，因此有：

图1-28　例1-2图

i（t）＝100cos（103t＋φi）；i（0）＝50＝100cosφi

解得：φ＝，由于最大值发生在计时起点右侧，故取：φ＝。

所以：i（t）＝100cos（103t-）

当103t1＝时，电流取得最大值，即：t1＝＝1.047 ms。

思考题：万用表测量正弦交流电压，读数是有效值吗？