直流电路的分析方法

直流电路分析

1.基尔霍夫定律

基尔霍夫定律包括基尔霍夫电压定律（KVL）和基尔霍夫电流定律（KCL）。它反映了电路中所有支路电压和电流所遵循的基本规律，是分析集总参数电路的根本依据。基尔霍夫定律与元件特性构成了电路分析的基础。在具体讲述基尔霍夫定律之前，先介绍电路模型图中的一些常用术语。

1）常用术语

（1）支路（branch）——电路中通过同一电流的分支。通常用b表示支路数。

一条支路可以是单个元件构成，亦可以由多个元件串联组成。如图1-14所示电路中有三条支路。

（2）节点（node）——三条或三条以上支路的公共连接点称为节点。通常用n表示结点数。如图1-14所示电路中有a、b两个结点。

（3）路径（path）——两节点间的一条通路。路径由支路构成。如图1-14所示电路中a、b两个结点间有三条路径。

（4）回路（loop）——由支路组成的闭合路径。通常用l表示回路。

如图1-14所示电路中有三个回路，分别由支路1和支路2构成、支路2和支路3构成、支路1和支路3构成。

（5）网孔（mesh）——对平面电路，其内部不含任何支路的回路称网孔。

如图1-13所示，电路中有两个网孔，分别由支路1和支路2构成、支路2和支路3构成。支路1和支路3构成的回路不是网孔。因此，网孔是回路，但回路不一定是网孔。

2）基尔霍夫电流定律（KCL）

KCL是描述电路中与结点相连的各支路电流间相互关系的定律。它的基本内容是：对于集总参数电路中的任意结点，在任意时刻流出或流入该结点电流的代数和等于零。用数学式子表示为：

图1-14所示为电路的一部分，对图中结点列KCL方程，设流出结点的电流为“＋”，流入结点电流为“-”，有：

-i1-i2＋i3＋i4＋i5＝0

或表示成：

i1＋i2＝i3＋i4＋i5

即：

则KCL又可叙述为：对于集总参数电路中的任意结点，在任意时刻流出该结点的电流之和等于流入该结点的电流之和。KCL方程是按电流参考方向列写，与电流实际方向无关。

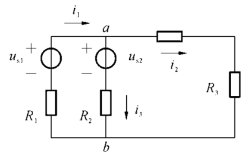
图1-13　电路结构示意图

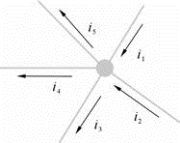
图1-14　结点电流示意图

3）基尔霍夫电压定律（KVL）

KVL是描述回路中各支路（或各元件）电压之间关系的定律。它的基本内容是：对于集总参数电路，在任意时刻，沿任意闭合路径绕行，各段电路电压的代数和恒等于零。KVL方程按电压参考方向列写，与电压实际方向无关。

用数学式子表示为：

（1）标定各元件电压参考方向。

（2）选定回路绕行方向，顺时针或逆时针。

对图1-15中回路顺时针方向，列KVL方程有：

-U1-Us1＋U2＋U3＋U4＋Us4＝0

或：

U1＋Us1＝U2＋U3＋U4＋Us4

应用欧姆定律，上述KVL方程也可表示为：

-R1I1＋R2I2-R3I3＋R4I4＝Us1-Us4

思考题：基尔霍夫电压定律（KVL）和电流定律（KCL），只适用于集总参数电路，结论对吗？

2.电阻的串联、并联和串并联

1）电阻串联

图1-16所示为n个电阻的串联，设电压、电流参考方向关联，由基尔霍夫定律得出电路特点。

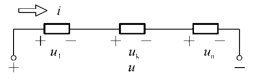
图1-15　回路电压示意图

图1-16　电阻串联示意图

（1）各电阻顺序连接。

根据KCL可知，各电阻中流过的电流相同；根据KVL，电路的总电压等于各串联电阻的电压之和，即：

u＝u1＋u2＋…uk＋…＋un

（2）等效电阻。

把欧姆定律代入电压表示式中得：

u＝R1i＋R2i＋…＋Rni＝（R1＋…＋Rn）i＝Reqi

其中等效电阻为：

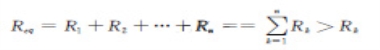
结论：

①电阻串联，其等效电阻等于各分电阻之和；

②等效电阻大于任意一个串联的分电阻。

（3）串联电阻的分压。

若已知串联电阻两端的总电压，则：uk＝Rki＝

满足：

u1∶u2∶…uk∶…∶un＝R1∶R2∶…Rk∶Rn

结论：

电阻串联，各分电阻上的电压与电阻值成正比，电阻值大者分得的电压大，因此串联电阻电路可作分压电路。

（4）功率。

各电阻的功率为：

P1＝R1i2，P2＝R2i2，…Pk＝Rki2，…Pn＝Rni2（公式有改动）

总功率为：

P＝Reqi2＝（R1＋R2＋…＋Rk＋…Rn）i2＝P1＋P2＋…＋Pn

结论：

①电阻串联时，各电阻消耗的功率与电阻大小成正比，即电阻值大者消耗的功率大；

②等效电阻消耗的功率等于各串联电阻消耗功率的总和。

2）电阻并联(www.xing528.com)

（1）电路特点。

图示为n个电阻的并联，设电压、电流参考方向关联，由基尔霍夫定律可得电路特点如下。

①各电阻两端分别接在一起，根据KVL知，各电阻两端为同一电压。

②根据KCL，电路的总电流等于流过各并联电阻的电流之和，即：

i＝i1＋i2＋…＋in

（2）等效电阻。

把欧姆定律代入电流表示式中得：

其中G＝1/R为电导。以上式子说明图1-17（a）所示多个电阻的并联电路与图1-17（b）所示单个电阻的电路具有相同的VCR，是互为等效的电路。

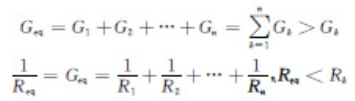
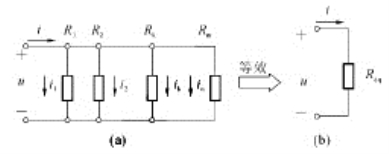
图1-17　电阻并联电路等效电阻

最常用的两个电阻并联时，求等效电阻公式：

结论：电阻并联，各分电阻上的电流与电阻值成反比，电阻值大者分得的电流小。因此并连电阻电路可作分流电路。

（3）功率。

各电阻的功率为：

P1＝G1u2，P2＝G2u2…，Pk＝Gku2…Pn＝Gnu2

总功率为：

P＝Gequ2＝（G1＋G2＋…＋Gk＋…Gn）u2＝P1＋P2＋…＋Pn

从以上各式得到结论：

①电阻并联时，各电阻消耗的功率与电阻大小成反比，即电阻值大者消耗的功率小；

②等效电阻消耗的功率等于各并联电阻消耗功率的总和。

3）电阻的串并联

电路中有电阻的串联，又有电阻的并联的电路称电阻的串并联电路。电阻相串联的部分具有电阻串联电路的特点，电阻相并联的部分具有电阻并联电路的特点。

求解串、并联电路的一般步骤如下：

①求出等效电阻或等效电导；

②应用欧姆定律求出总电压或总电流；

③应用欧姆定律或分压、分流公式求各电阻上的电流和电压。

因此分析串并联电路的关键问题是判别电路的串、并联关系。

思考题：电阻的串联电路中，分压值与电阻值成正比，结论对吗？

3.电压源、电流源的串联和并联

电压源、电流源的串联和并联问题的分析是以电压源和电流源的定义及外特性为基础，结合电路等效的概念进行的。

1）理想电压源的串联

图1-18所示为n个电压源的串联，根据KVL得总电压为：

注意：式中usk考方向与us的参考方向一致时，usk在式中取“＋”号，不一致时取“-”号。

根据电路等效的概念，可以用图1-18（b）所示电压为us的单个电压源等效替代图1-18（a）中的n个串联的电压源。通过电压源的串联可以得到一个高的输出电压。

2）理想电压源的并联

图1-19所示为n个电压源的并联，根据KVL得：

us＝us1＝us2＝…＝usn（公式有改动）

上式说明只有电压相等且极性一致的电压源才能并联，此时并联电压源的对外特性与单个电压源一样，根据电路等效概念，可以用图1-19（b）所示的单个电压源替代图1-19（a）所示的电压源并联电路。注意：①不同值或不同极性的电压源是不允许并联的，否则违反KVL；②电压源并联时，每个电压源中的电流是不确定的。

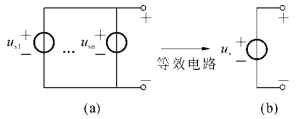
图1-18　理想电压源的串联

图1-19　理想电压源的并联

3）理想电流源的并联

图1-20所示为n个电流源的并联，根据KCL得总电流为：

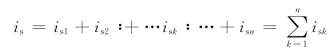
注意：式中isk的参考方向与is的参考方向一致时，isk在式中取“＋”号，不一致时取“-”号。根据电路等效的概念，可以用图1-20（b）所示电流为is的单个电流源等效替代图1-20（a）中的n个并联的电流源。通过电流源的并联可以得到一个大的输出电流。

图1-20　电流源的并联

4）理想电流源的串联

图1-21所示为n个电流源的串联，根据KCL得：

is＝is1＝is2＝…isn（公式有改动）

上式说明只有电流相等且输出电流方向一致的电流源才能串联，此时串联电流源的对外特性与单个电流源一样，根据电路等效概念，可以用图1-21（b）所示的单个电流源替代图1-21（a）所示的电流源串联电路。注意：①不同值或不同流向的电流源是不允许串联的，否则违反KCL；②电流源串联时，每个电流源上的电压是不确定的。

图1-21　理想电流源的串联

5）实际电压源和电流源的等效变换

图1-22所示为实际电压源、实际电流源的模型，它们之间可以进行等效变换。

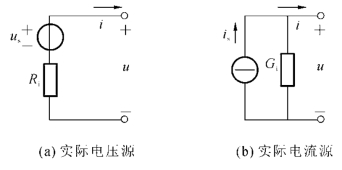
图1-22　实际电压源和实际电流源

由实际电压源模型得输出电压u和输出电流i满足关系：

u＝us-Rii

由实际电流源模型得输出电压u和输出电流i满足关系：

i＝is-Giu

比较以上两式，如令：

则实际电压源和电流源的输出特性将完全相同。根据电路等效的概念，当上述两式满足时，实际电压源和电流源可以等效变换，如图1-23所示。

图1-23　电流源转换为电压源

需要注意的是：①理想电压源与理想电流源不能相互转换，因为两者的定义本身是相互矛盾的，不会有相同的VCR。②电源互换是电路等效变换的一种方法，这种等效是对电源以外部分的电路等效，对电源内部电路是不等效的。③电源等效互换的方法可以推广应用，如把理想电压源与外电阻的串联等效变换成理想电流源与外电导的并联，同样可把理想电流源与外电阻的并联等效变换为电压源形式。

思考题：只有电压相等且极性一致的电压源才能并联，结论对吗？