支承柱的布置、调整和减小变形量的方法

可以通过在后固定板和支承板之间使用支承柱来明显减少板的变形。合理直接安放在型腔下部的支承柱可以明显承受作用力。通过直接支承模具板，支承柱近处的剪切应力和弯曲明显减小。

图12.13所示为一个典型的设计方法。在这一设计中，推板和推杆固定板之间有一间隙。用销钉固定好支承柱使其中心与后固定板上的孔配合。用内六角圆柱头螺钉将支承板固定在后固定板上，那么支承柱将可以完全牢固地安装在模具上。

然而，支承柱的位置可能与其他的部件如推杆冲突。因此，不同设计布局和尺寸的支承柱应具体分析。如果模具变形影响较大，则应调节推杆的布局腾出空间来在合理的位置布置一些大的支承柱。图12.14所示的设计可以布置三个支承柱。左边推板外侧可以布置两个小的支承柱。支承柱应根据Bezel跨度合理布置。然而，若没有重新布置推杆，支承柱就不能直接安置在Bezel面下面。

另一个设计是在模具中心设计一个大的支承柱从而避免与推杆发生干涉。然而，成型时模具板的弯曲大多是因为模具左侧和右侧的载荷，故这一支承柱并不能很明显地解决模具板的变形问题。另外，这一设计可能会与经常使用的在成型机中间设置的推杆相冲突。另一种选择是在右边布置一个大小合适的支承柱。这一设计需要的支承柱比前一种少，但是在支承柱和推出导轨间有很大的跨度从而会产生更大的变形。

下面将分析使用支承柱的数目、位置和尺寸。分析的一个复杂问题是支承柱是具有有限直径和刚度的结构元件，也就是在压缩力的作用下会发生变形。型芯和支承板也会随之发生变形。另外，支承柱和推出导轨之间的型芯和支承板会发生弯曲。为了计算板的总变形量，要将压缩和弯曲的变形量进行叠加。这一原理如图12.15所示。

为了便于分析，模具中的力必须转换成适用于手工分析的一组载荷。图12.16所示为作用在型腔壁上的熔体压力转换后的压缩载荷和弯曲载荷情况。总的作用力F为作用在型腔长度方向和宽度方向上的综合熔体压力。为了计算弯曲变形，力F分为两部分作用在支承柱和推出导轨跨度的中间。平衡力由支承柱和推出导轨来提供。

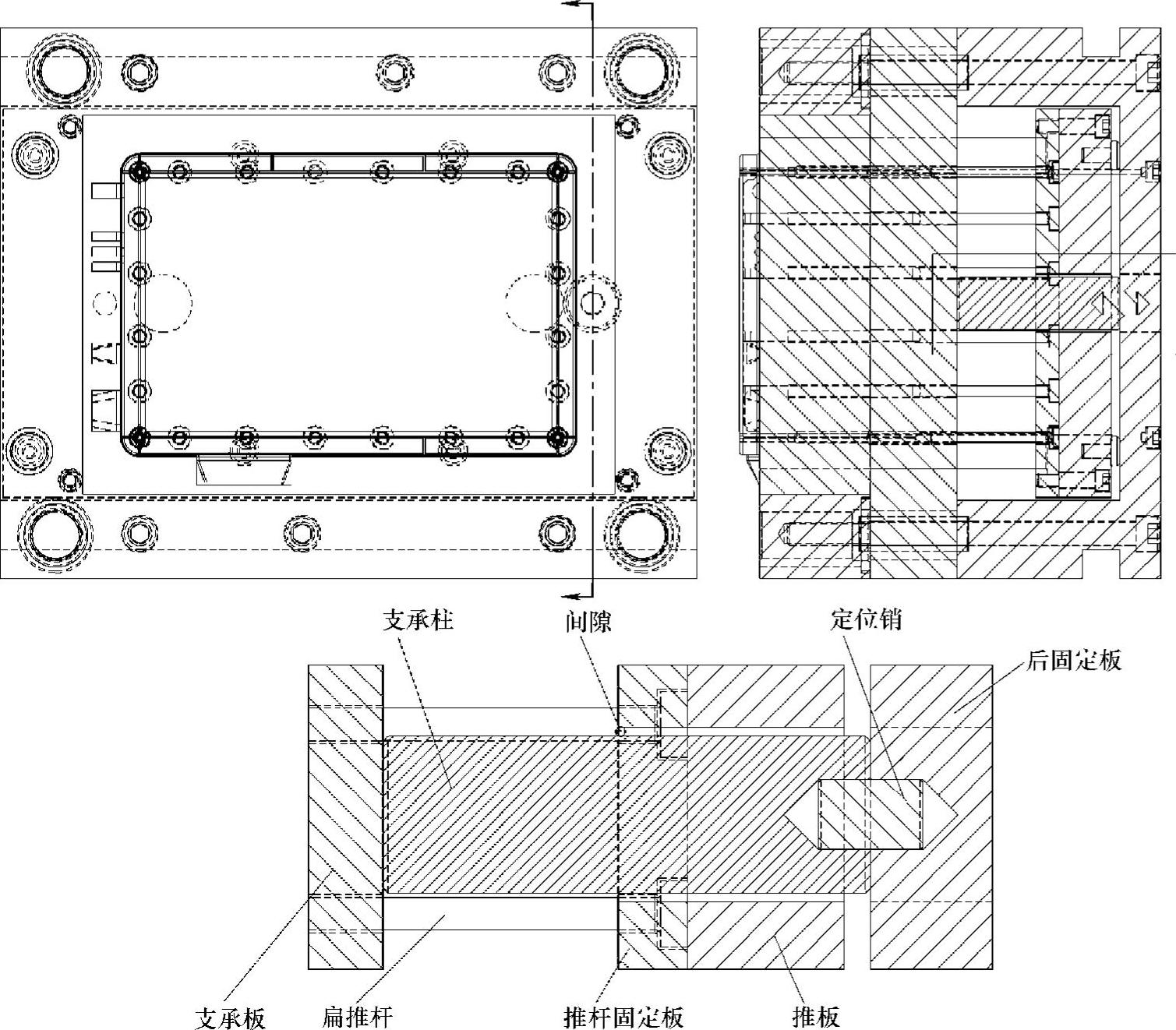
图12.13 带支承柱的典型模具设计

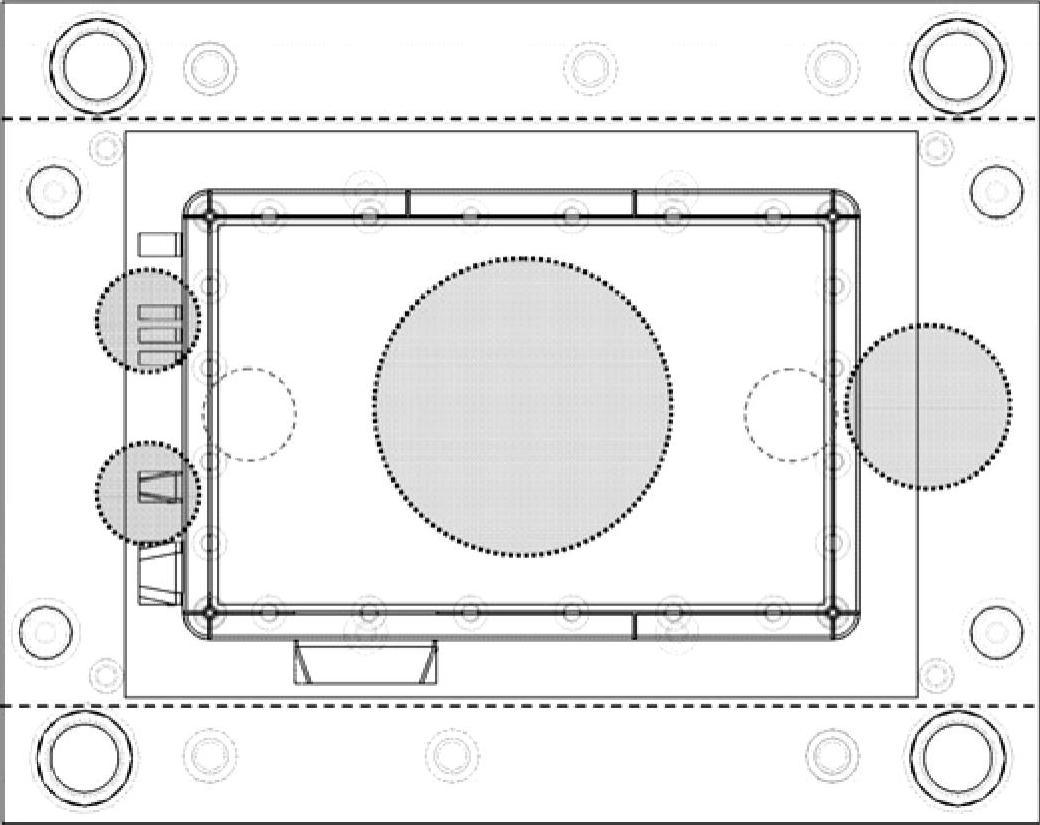
图12.14 不同的支承柱位置

图12.15 压缩变形量与弯曲变形量的叠加

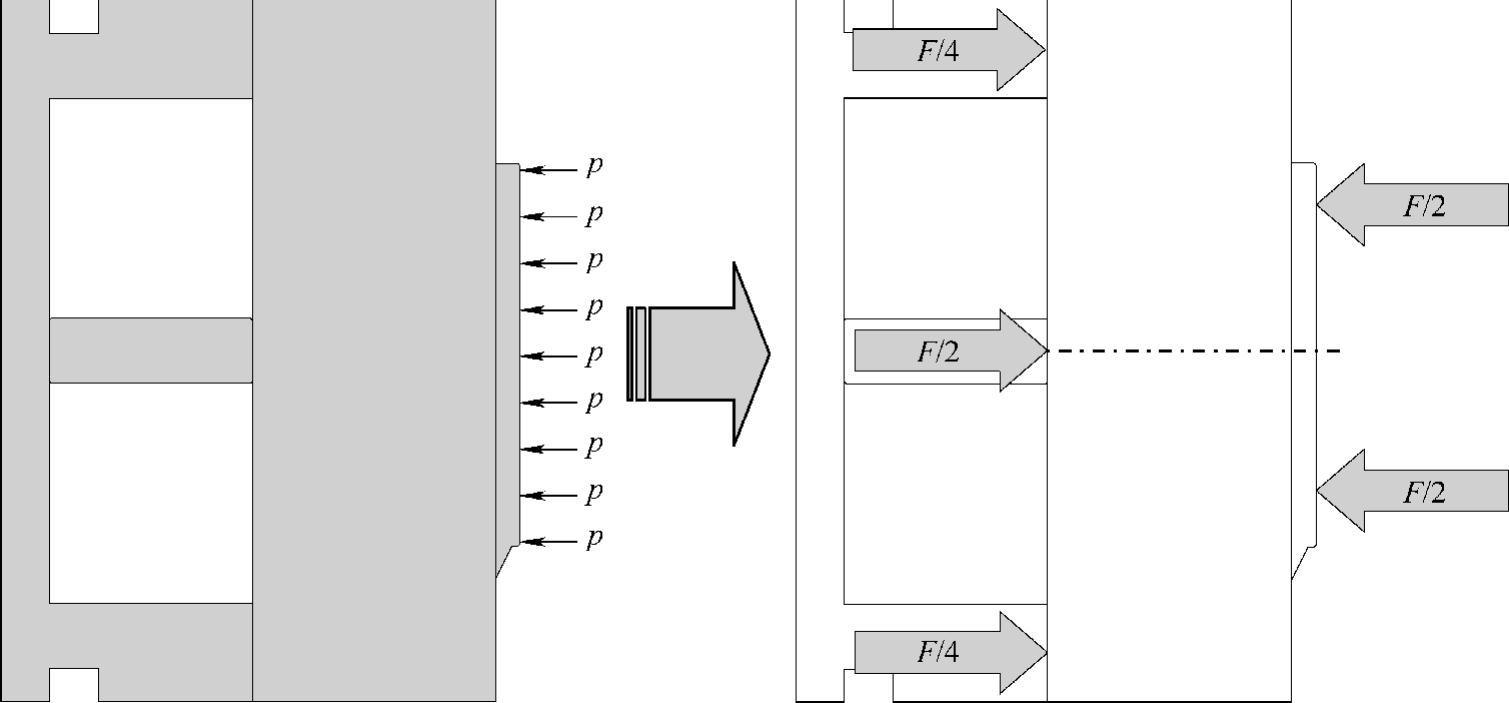
图12.16 压缩载荷与弯曲载荷情况

应用叠加法分解作用力之后，就可以用前面介绍的压缩变形和弯曲变形分析来计算支承柱中的应力σ、压缩变形δ_compression和弯曲变形δ_bending了。型腔壁的变形量可以用到支承柱中心线的距离χ的公式来计算，即

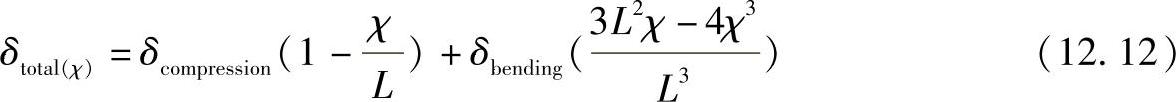
式中，L是从支承柱到推出导轨的跨度；χ的范围是跨度的一半。

模具的最大变形发生在支承柱中心处或支承柱和推出导轨的中间处，其取决于各变形量的数量级。从而压缩和弯曲叠加时的最大变形量计算公式为

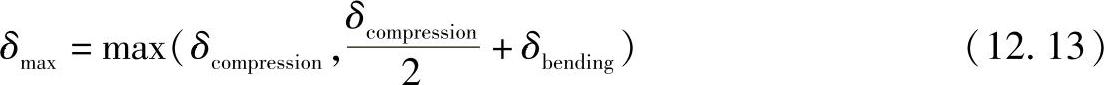(www.xing528.com)

例：为Bezel模具设计一支承柱使总变形量小于0.1mm。分析支承柱中的应力和最终变形量。

支承柱在Bezel一侧下面支承型芯和支承板，图12.17所示为型腔局部的分析图。Bezel的顶部和底部接近推出导轨所以没有明显的板的弯曲变形。

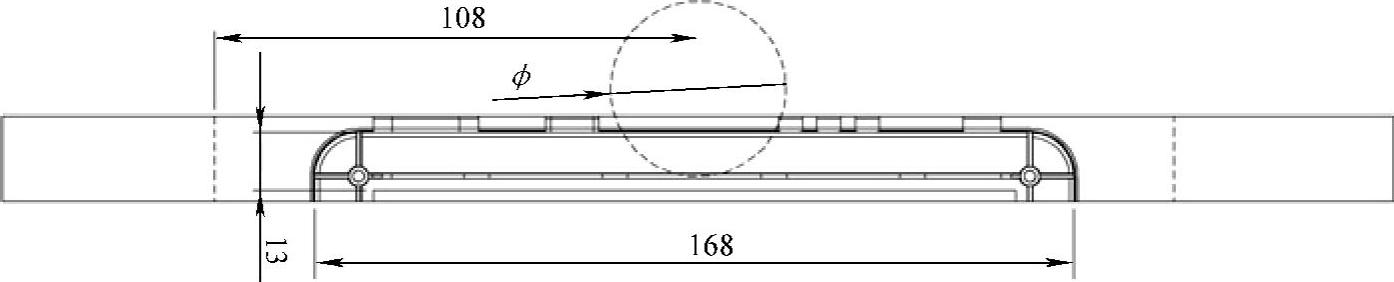
图12.17 支承柱局部区域的模具型腔面积

假定熔体压力为150MPa，作用在这一部分模具上的总作用力为

F=pA=150×168×13N=327600N=33tf

其为一个很大的作用力。先假定支承柱的直径为37.5mm来分析。假设支承柱传递一半的作用力，那么支承柱中的应力为

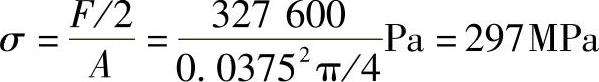
如果制作支承柱的材料为SAE1040钢^[3]，则这一应力接近其疲劳极限。最终应变为

支承柱的长度为89mm（3.5in），最终变形量为

δ_compression=εL=0.14%×88.9mm=0.13mm

其远远大于设定的最大变形量0.1mm。为了减小变形量，支承柱的直径增大到50mm。因此应力相应减小到167MPa而压缩产生的变形量相应减小到0.07mm。

弯曲的分析与前一例子非常相似。然而，模板的有效作用宽度保守估计为型腔的宽度（13mm）。其惯性矩为

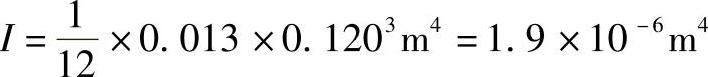
因为使用了支承柱，跨度从图12.11中的216mm减小到图12.17中的108mm。应用弯曲的计算公式计算作用在模具这一部分的作用力为33t时的弯曲变形量为

因弯曲产生的变形量很小，由支承柱压缩引起的最大变形将发生在模具的中心处。值得注意的是在满足变形要求情况下，后模板和（或）支承板的厚度可以适当减小。另外，通过先装配支承柱可以大大减小压缩产生的变形。特别的，可以使用长度为88.97mm的支承柱（88.9mm加上0.07mm）在压缩变形时就回到正常所需的88.9mm，从而使型腔在成型过程中变浅。