估计地层各向异性收缩特性

一些材料如液晶聚合物和玻璃填充聚合物，呈现的材料性质取决于流动方向。对于这些各向异性材料，在填充和保压阶段，分子或纤维可在流动区域定向，如图10.6所示。图中通过长径比和椭圆的方向显示说明，贯穿厚度的取向非常复杂。填充和保压阶段的剪切流动会趋于取向于贯穿相当部分厚度的塑料熔体的流动方向。

各向异性材料在各主方向上呈现出不同的性质。例如，一种玻璃填充材料会在原则流动方向上比其他方向呈现更少的收缩。其强度的提高是由于填充了更高强度的玻璃纤维，而玻璃纤维取向于流动方向。因为玻璃有更低的热膨胀系数，因此材料也会在流动方向上比其他方向有更小的收缩。体积和各向异性线性收缩之间的关系如图10.7所示，其中变量a表示流动方向上与其他两方向相关的各向异性分数。

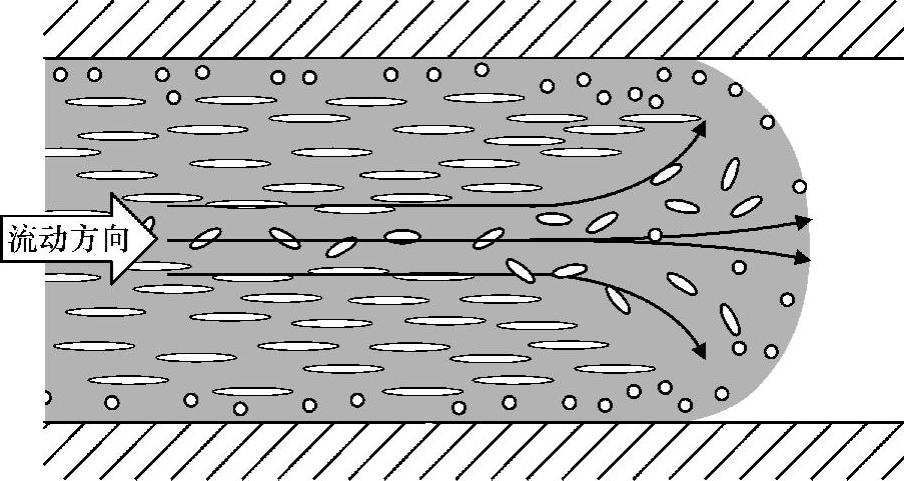
图10.6 取向导致各向异性

图10.7 体积和各向异性收缩

按照之前的各向同性材料收缩的推导，各向异性收缩的收缩立方体体积为

L³r_v=L³（1-s）²（1-as） （10.14）

得到立方方程为

as³-（2+a）s²+（2+a）s-（r_v-1）=0 （10.15）

这个立方方程可以解析计算，可以通过方程迭代很容易地得到其解为

例：假设ABS用于成型框架注射制品，材料中有15%（体积分数）的玻璃纤维（材料牌号为Cycolac CRT3370）。如果已知塑料材料在流动方向上的收缩是其他方向收缩的一半，估算其各向异性收缩。(www.xing528.com)

体积分数为15%的玻璃纤维会减小体积收缩，因为玻璃比塑料有更低的热膨胀。玻璃的密度为2600kg/m³，未填充或“纯”ABS的密度为1040kg/m³，玻璃纤维在ABS中的体积为

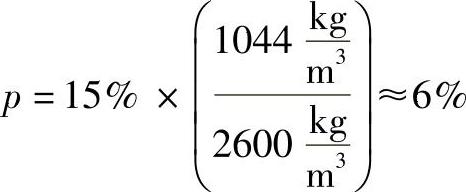
这说明填充塑料的94%有明显收缩，而塑料的6%不会有明显的收缩。此减小的压缩性说明了收缩体积的减小为

Δ_v=94%×0.09×10^-4m³/kg=0.085×10^-4m³/kg

因此收缩体积相对变化为

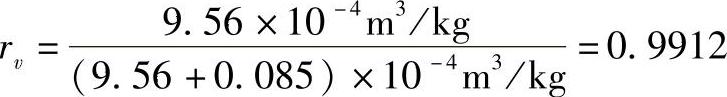
各向异性分数a为0.5。为迭代计算各向异性收缩，需要预估收缩。因为收缩很小，且式（10.16）非常稳定，零收缩的预估计应该是足够的。首先迭代式为

将收缩0.00352用于另一迭代式中，即

两次迭代后，得到解。收缩s在厚度方向上等于0.35%，流动方向的收缩as为0.18%。