压缩行为模型解析的介绍，

聚合物熔体的压缩（或pvT）行为可以通过双域Tait方程模拟，它描述了比体积v与熔体压力和温度的函数关系。其“双域”是指对比体积在固体和熔体两个阶段分别进行模拟。固态和熔融态之间的转变温度是与压力相关的函数，即

T_t（p）=b₅+b₆p （10.2）

式中，b₅是压力为0时的转变温度；b₆是转变温度与压力有关的变化率。

对于转变温度以下的温度，相关比体积为v₀（T）和压缩系数为β，模型为

v₀=b_1，s+b_2，s（T-b₅）

β（T）=b_3，sexp[-b_4，s（T-b₅）] （10.3）

式中，b_1…4，s是材料在固态时相关特性的材料系数。

对于高于转变温度的温度，相关比体积和压缩系数模型为

v₀=b_1，m+b_2，m（T-b₅）

β（T）=b_3，mexp[-b_4，m（T-b₅）] （10.4）

式中，b_1…4，m是材料在熔融态时相关特性的材料系数。

那么比体积与压力和温度之间的函数关系为

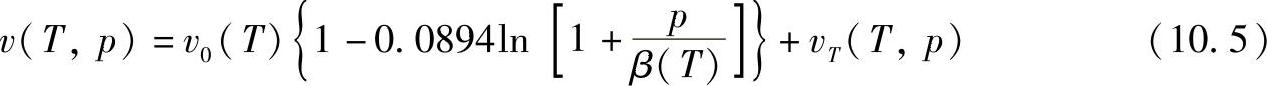(www.xing528.com)

式中，v_T是从紧密堆积的半结晶聚合物到更疏松堆积的无定形聚合物转变相关的额外比体积，这个转变比体积模型为

v_T（T，p）=b₇exp{b₈[T-T_t（p）]-b₉p} （10.6）

双域Tait方程的系数对于许多聚合物是合理的。附录A提供了一些不同聚合物的模型系数。ABS（Cycolac MG47）的比体积与温度在三种不同压力条件下的关系如图10.2所示。图10.2说明，随着熔融温度的升高，聚合物熔体膨胀，比体积增加。当施加压力时，聚合物熔体被压缩，比体积减小。通过pvT图可以提取许多有用的信息。首先，室温零压条件下的比体积近似为0.955cm³/kg。这说明密度ρ为

此值与材料提供者给的密度值1044kg/m³非常相近。体膨胀系数CVTE是比体积与温度相关的改变。从图中，CVTE可以计算为

正如要讨论的，CVTE直接与线膨胀系数和收缩相关。

材料的压缩系数β也可以通过pvT图计算，比体积的改变率与压力相关，即

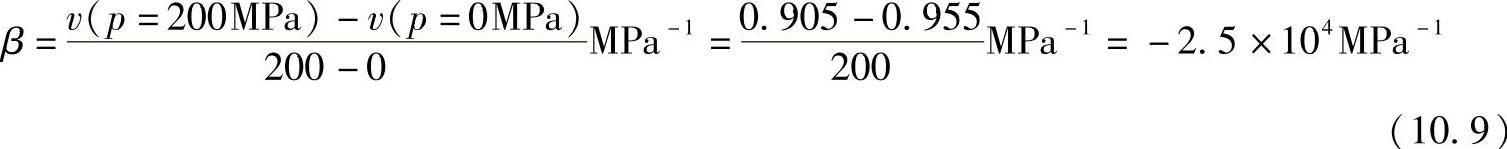
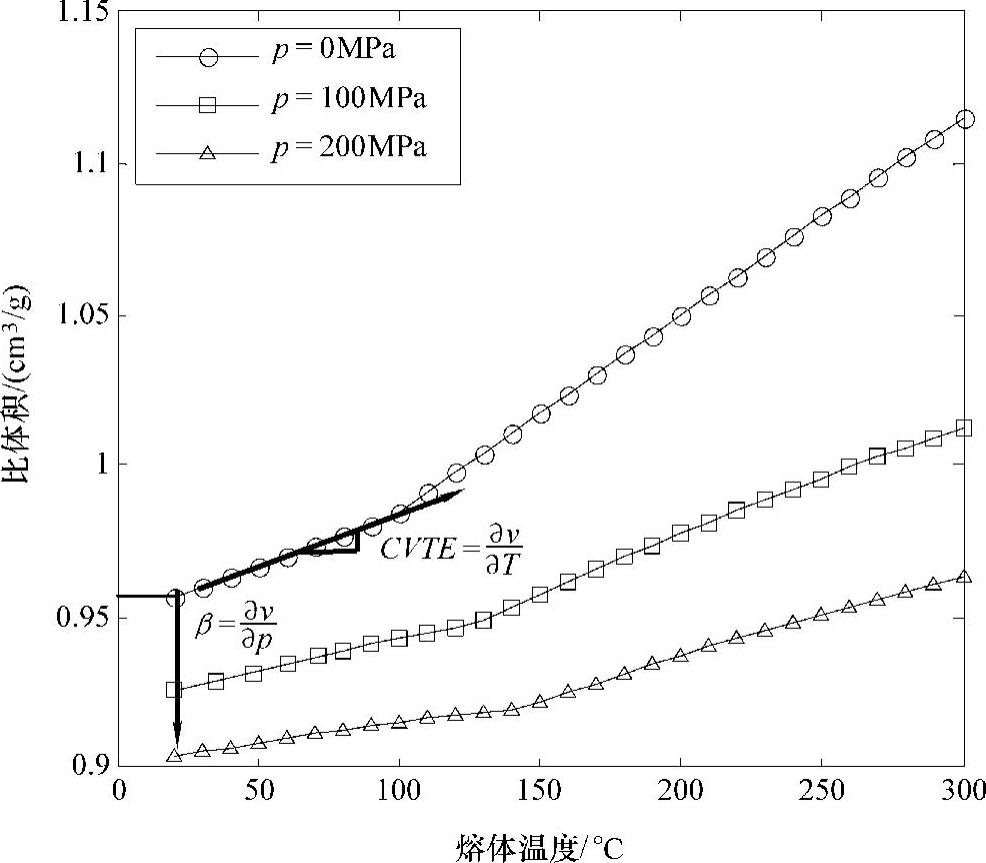
图10.2 ABS的pvT行为

从图10.2中发现，与聚合物热膨胀和压缩相关的系数在熔融态比固态时更大。原因是聚合物随着温度的提高在熔融态比固态时有更大的原子能。这其中所提高的能量提供了更多的围绕分子的“自由体积”，并增加了聚合物的热膨胀和压缩。