计算冷却所需时间的方法

冷却时间定义为充满型腔的塑料由熔融到变得足够硬以至于可以推出所需的时间。以下理论为确定最小冷却时间提供了理论支持^[1]。因为型腔充满之后，熔体流量变得非常小（热量对流也非常小），在塑料和模具之间传递的热量由瞬时热传导方程支配，即

式中，a是热扩散率，定义为

式中，T是温度；t是时间；z是厚度方向的尺寸；k是热导率；ρ是密度；c_p是比热容。热扩散率本质上是测试材料相对于其本身所能储存热量的传热能力。对于更快的热传导，需要具有更高热扩散率的模具材料，这些材料（如铝）相对于钢具有较低的力学性能，如图4.25所示。

瞬时热传导方程即式（9.2）是一个二级、抛物线、微分方程。对于盘和棒这种简单几何形状的物体，人们开发了一种瞬时热传导解析法。在型腔中心线处的熔体温度可以通过级数扩展来预估，即

公式中考虑了六个参量，模具型腔中心线处的塑料温度是冷却时间的函数，如图9.1所示。注射制品中心的塑料温度等于冷却过程中的初始熔体温度。在延迟2s后，型腔中心的熔体开始冷却。最后，塑料降温到模具温度。

为了确定冷却时间，需要提供一些标准以说明什么时候制品变得足够硬以适合推出。一个可行的方法是考虑材料的弹性模量，就是对材料抵抗挠度进行测试。材料冷却时的有效弹性模量如图9.1右边的纵轴所示。可以发现，当塑料熔体的温度接近模具温度时，弹性模量也接近一个固定值。材料刚度符合要求时的温度称为热变形温度（HDT）或欠载挠曲温度（DTUL），其可以通过标准测试（如ASTM D648）得到。

式（9.4）是冷却时间同熔体、冷却介质和推出温度之间的函数。模板的理论最短冷却时间为

式中，h是壁厚；T_eject是指定推出温度（通常表示为DTUL）；T_coolant是冷却温度；T_melt是熔融温度。对于棒状制品，理论最短冷却时间为

当计算冷却时间时，模具设计者应该考虑最厚的部分，因为其需要的固化时间最长。

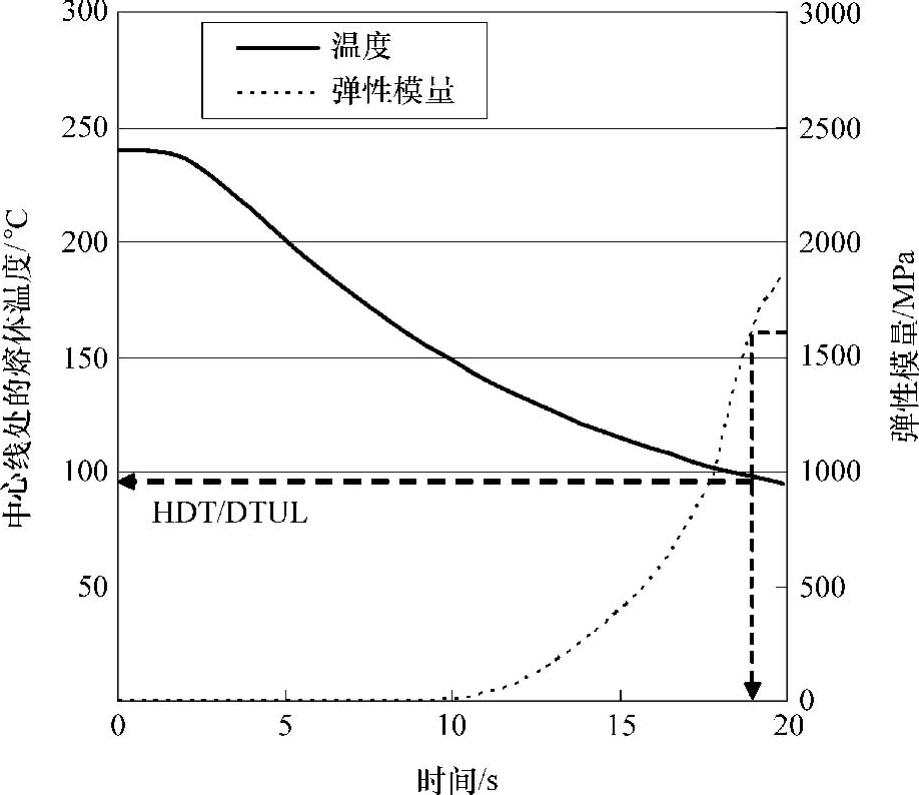
图9.1 中心线处的熔体温度变化

例：估算用于生产杯子和杯盖的两腔成套制品模具的冷却时间。

杯盖的公称厚度是2mm，杯子的公称厚度是3mm，主通道的直径是6.25mm。假设制品材料是ABS，熔融、冷却和推出温度分别是239℃、60℃和96.7℃，那么模具每一部分的冷却时间为

此结果提供了一些重要的信息。首先，因为杯子和杯盖厚度不同，模具中杯子部分需要更长的循环时间。如果不同壁厚的零件需要高质量生产，那么应用两个不同的模具采用不同的循环时间分别进行生产和设计则更加经济。然而，这种模具设计原则放弃了颜色匹配和压制组装，这对设计多腔成套制品模具是十分有利的。

其次，通道的冷却时间比杯子更长。实际上，通道不需要同零件冷却到硬度一样时脱模，因此根据以上计算得到的通道需要的冷却时间可以小于22.9s。但是，结果说明，循环时间受通道的冷却时间支配，因此缩小通道直径很重要，这不仅可以节省材料而且可以保证生产成型工艺。(www.xing528.com)

为验证以上的冷却分析，对壁厚为3mm的成型件的瞬时热传导进行了数字模拟。模拟假设塑料初始在熔融温度，与钢制模具型腔壁接触处的塑料温度总是处在冷却温度。如上所述，假设材料为ABS，熔融、冷却和推出温度分别为239℃、60℃和96.7℃。不同时间下贯穿制品壁厚的塑料温度如图9.2所示。在冷却开始时，塑料温度是熔融温度。根据分析，模具型腔壁处的塑料温度将立即降到冷却温度。热量从塑料传向模具，塑料的温度随之降低，直到模具中心冷却到冷却温度。

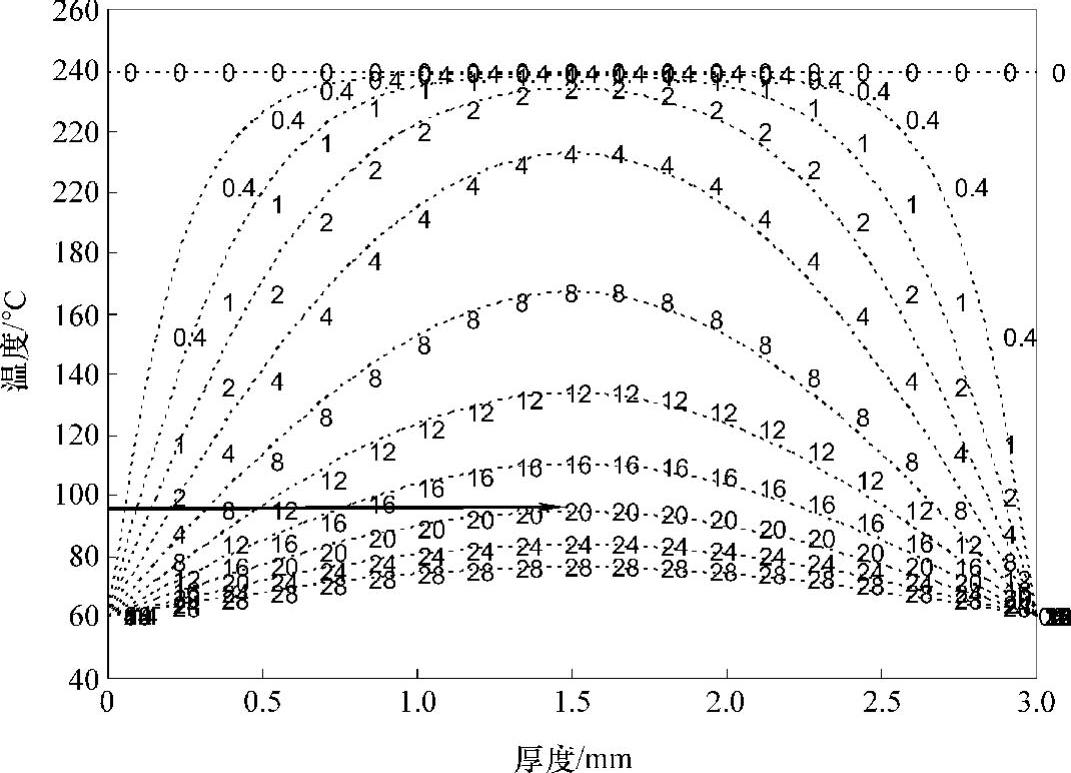
图9.2 塑料的冷却（等温边界）

在冷却期间，塑料制品必须足够坚硬以能够承受推出力。中心线的温度降到指定推出温度以下所需的时间可以通过图9.2预估。^[2]图9.2所示的模拟结果证实了前面所分析的结果，中心线推出温度为97℃时，冷却时间将接近19s。

这些结果是以模具壁等温为边界条件的，意思是模具壁处的塑料立即降到了模具冷却温度。实际上，模具钢不能承受很快的温度变化。因此，模具钢附近温度会提高。这种行为可以用对流边界条件来建模，即

式中，h_c是模具界面的聚合物从熔融至冷却的表面传热系数。之前的研究[29]说明注射制品中的表面传热系数等级为1000W/（m²·℃）。在对流边界条件下所模拟的温度变化如图9.3所示。

根据对流边界条件，模具壁处的塑料需要额外的时间降低到模具冷却温度。较慢的热传导限制了注射制品中心的冷却。如果心部必须达到指定的温度97℃，那么冷却时间应该更接近24s，而不是根据假设模具壁温度而预测得到的19s。

图9.3 塑料的冷却（对流边界）

另外，在塑料工业中有条通用准则，就是冷却时间可以大致计算为

式中，h是壁厚，单位为mm。

例：应用式（9.8）估算壁厚为3mm的制品的冷却时间。

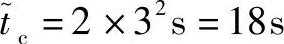
该结果同之前的19.2s（假设理想传导）和24s[假设表面传热系数等级为1000W/（m²·℃）]分析结果形成了很好的比较。

式（9.8）提供了一个很接近的结果，原因是大多数热塑性塑料热扩散率的等级为9×10^-5m²/s，加工温度（T_melt-T_coolant）/（T_coolant-T_eject）在5左右。把这些相应值代入式（9.5）中得到

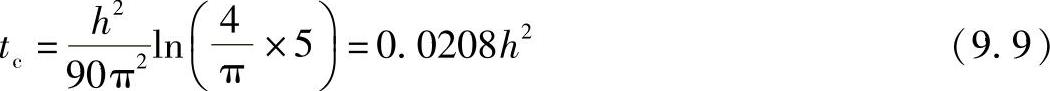
式（9.8）提出的规则非常好地与式（9.9）的典型热传导分析相匹配。而式（9.8）是一个最优指导，其对于应用式（9.5）和式（9.6）估算冷却时间以明确应用设计、材料特性和加工条件是一个的好方法。同时需要注意的是通过式（9.9）估算的冷却时间约是之前通过式（3.24）估算的循环时间的一半。