正弦交流电路相量分析的计算方法

正弦交流电路分析

复阻抗类似直流电路的电阻元件。结合基尔霍夫定律和欧姆定律的相量形式，只要把直流电路的电压、电流换成交流电路的电压、电流相量；把直流电路的电阻换成交流电路的复阻抗，那么在基尔霍夫定律和欧姆定律基础上建立的直流电路的所有公式、定理和分析方法，就全部适用于正弦交流电路的分析计算。

【特别提示】

① 数学运算是复数的运算。

② 可以利用相量图来帮助分析计算电路。

例4.16　电路如图4-45所示，已知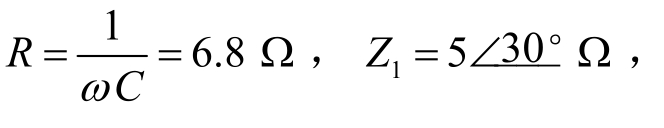外加电压，求电流及电容电压。

图4-45　例4.16用图

解　等效复阻抗

电容电压为

电容电压也可用分压公式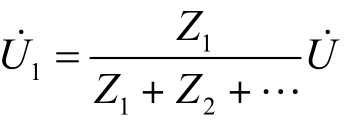求得，即

例4.17　如图4-46（a）所示，已知R1=36Ω，R2=75Ω，ωL=15Ω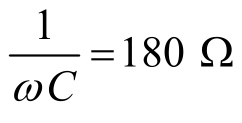，，电流源电流。求等效复阻抗Z以及电流。

解　这是一个复阻抗并联电路，作出等效电路如图4-46（b）所示，则

图4-46　例4.17用图

根据两个电阻的并联公式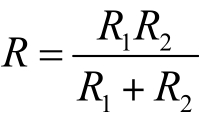，则等效复阻抗为

根据两个电阻的分流公式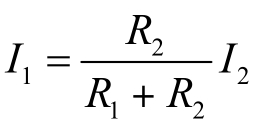，则各支路电流相量为

练习：若确定交流电流源的电压（设电流源的电压和电流关联参考方向下），该如何分析？

例4.18如图4-47（a）所示，已知0.1+j0.5Ω，Z3=5+j5Ω。试用支路电流法、叠加定理、戴维南定理求电流。

图4-47　例4.18用图(www.xing528.com)

解　（1）支路电流法。

本题两个节点，列写一个节点KCL电流方程；两个网孔，列写两个KVL方程，绕行方向取顺时针方向。方程为

代入已知数据，有

（2）叠加定理。

① 单独作用，如图4-47（b）所示。

② 单独作用，如图4-47（c）所示。

（3）戴维南定理。

① 去掉待求支路，得图4-47（d），确定端口开路电压U˙OC。

② 确定等效复阻抗Z0，即

③ 图4-47（e）所示为原电路的等效电路，有

思考题

（1）RLC串联电路中电阻上电压为，电感上电压，电容上电压，求电源电压，并指出电路的性质。

（2）已知电路的端电压，通过的电流，求电路的复阻抗Z，并指出电路的性质。

（3）RLC串联电路中，已知电阻R=36Ω，电感元件的感抗XL=20Ω，电容元件的容抗XC=68Ω。求电路的复阻抗Z，并指出电路的性质。若电源频率增大10倍，复阻抗Z和电路的性质会发生变化吗？若变化，应该是多少？

（4）已知一电路的复阻抗Z=10∠-4-5-°Ω，求该电路的等效电阻R和等效电抗X。

（5）已知两个复阻抗Z1=60+j80（Ω），Z2=120+j160（Ω）。计算Z1和Z2串联等效复阻抗Z串和并联等效复阻抗Z并分别是多少？