非正弦周期信号测试分析

正弦交流电的叠加

图4-26　直流电压和交流电压的叠加

在电工技术中，除了电压和电流是时间的正弦函数外，还会遇到不按正弦规律变化的电压和电流，即非正弦量。无线电和通信技术中传送的电信号、自动控制以及电子计算机中大量使用的脉冲信号等都是非正弦量；发电机、变压器等电气设备的电压、电流也不是纯粹的正弦量。所有这些非正弦量可以分为两大类，即周期的和非周期的。电力系统中所遇到的正弦周期量一般不含恒定分量，这样的非正弦周期量又称为非正弦交流量。下面对非正弦周期量进行分析。

1.非正弦周期信号的傅里叶级数表达式

1）直流电压和交流电压的叠加

在许多实际电路中，交流电压和直流电压是结合在一起的。例如，在放大电路中，交流信号就叠加在直流工作电压上。这是叠加定理最普遍的应用。

图4-26所示为一个直流电压源Us和一个交流电压源us串联，即一个直流电压基础上的交流电压。

如果Us比正弦电压的峰值大，这个相加的电压就是一个不会发生正负极性翻转的正弦波，用示波器观看如图4-27（a）所示，正弦波叠加在直流电压上；如果Us比正弦电压的峰值小，如图4-27（b）所示，正弦波将在其下半周部分中出现负值。在这种情况下，正弦波都将达到一个最大值电压Us+Um和一个最小值电压Us-Um。

图4-27　示波器显示波形

2）非正弦周期波信号的傅里叶级数表达式

（1）非正弦周期波的合成。

图4-28所示为将不同频率的电压源叠加在一起。XSC2示波器2的A通道显示的是u1和u3这2个不同频率正弦交流电压的叠加，产生一个非正弦周期波，即马鞍波形；XSC1示波器1的B通道显示的是u1、u3、u5、u7、u9等5个不同频率正弦交流电压的叠加，产生的非正弦周期波类似于方波。由此可见，将不同频率的正弦波叠加可形成非正弦周期波。通过XSC1示波器1的B通道显示的波形会发现，叠加更多的不同频率正弦交流电压分量，波形更接近方波。

图4-28　奇次谐波产生的方波

（2）非正弦周期波的分解——傅里叶级数表达式。

从数学知识可以知道，如果一个周期函数f （t）满足狄里赫利条件（电工电子技术中常见的周期函数都满足这一条件），就可以分解展开为傅里叶级数，即

式中　A0——直流分量或恒定分量；

A1msin（ωt+φ1）——基波或一次谐波分量；

ω——基波角频率，；

T——非正弦周期函数f （t）的周期；

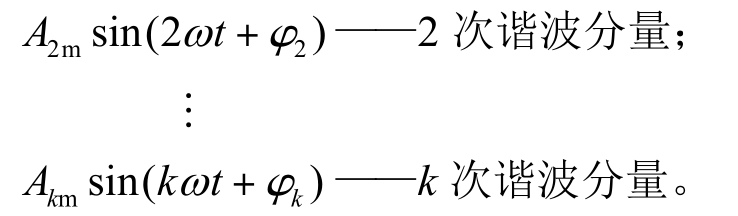
当k≥2时，统称为高次谐波分量。

式（4-25）说明，一个非正弦周期函数等于一个常数项和无穷多项不同频率的正弦函数之和。k为奇数的谐波称为奇次谐波，k为偶数的谐波称为偶次谐波。

在图 4-28 中，基波 u1 的角频率是 ω=1 000 rad/s，3 次谐波 u3 的角频率是 3ω =3 000 rad/s，5次谐波u5的角频率是5ω=5 000 rad/s……

在实际运算中，f （t）可以是电压u（t）或电流i（t），于是有

将一个非正弦周期波分解为直流分量与无穷多个不同频率的谐波分量之和，称为谐波分析法。理论上的傅里叶级数是一个无穷级数，理论上要取无限项才能准确表示原周期函数，但实际应用时，由于其收敛很快，较高次谐波的振幅很小，因此只需取级数的前几项进行计算就足够准确了。

在分析电路时，一个具体的非正弦周期波如何分解为傅里叶级数，可以查阅相应的电工手册。表4-1列出了电工技术中常见的几种典型波形的傅里叶级数展开式。

表4-1　几种典型非正弦周期波的傅里叶级数

续表

2.非正弦周期信号的有效值和平均值

1）非正弦周期信号的有效值

非正弦周期信号的有效值定义和正弦周期信号的有效值相同。有效值的定义式为

设周期电流为

将其代入有效值的定义式，得(www.xing528.com)

将上式方括号内各分量之和的平方展开，包含下列各类项：

①

②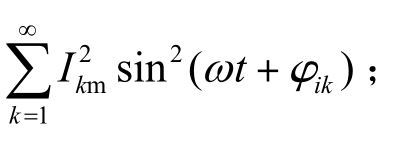

③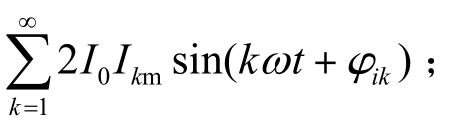

④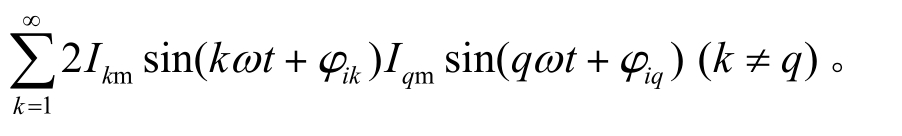

于是根号内各项的值为

①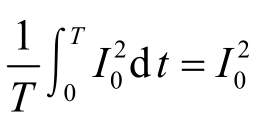

②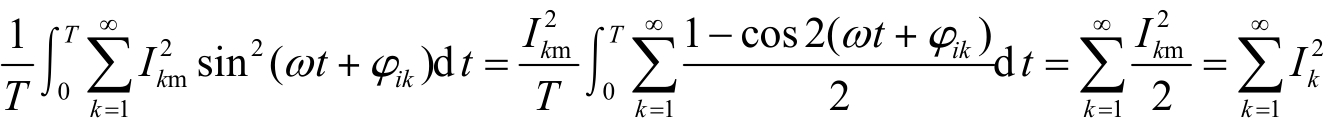

③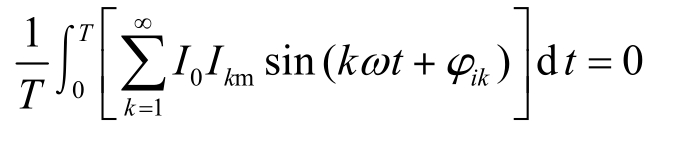

④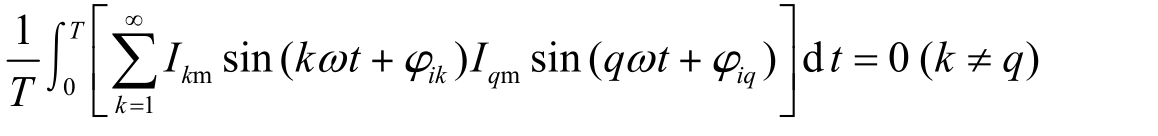

所以，非正弦电流的有效值计算公式为

式中　I0——直流分量；

I1——基波分量的有效值，；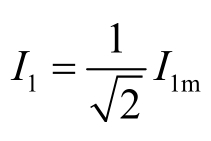

I2——2次谐波分量的有效值，；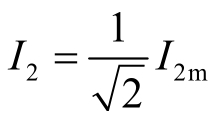

⋮

Ik——k次谐波分量的有效值，。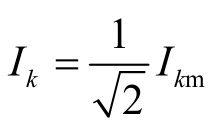

类似地，一个非正弦周期电压的有效值可以用下式计算

因此，非正弦周期量的有效值等于直流分量和各次谐波分量有效值的平方和的平方根。

2）非正弦周期信号的平均值

除有效值外，非正弦周期量有时还引用平均值。非正弦周期信号的平均值定义和正弦周期信号的平均值相同：周期量的绝对值在一个周期内的平均值，即

若采用数学的平均值概念，当一个周期内其值均为正值的周期量时，非正弦周期量的平均值是它的直流分量，以电流为例，有

不同类型的电工测量仪表，其指针的偏转原理是不同的。磁电系仪表的偏转角正比于电流的恒定分量，电磁系和电动系仪表的偏转角正比于电流的有效值，而全波整流系仪表的偏转角与电流的平均值成正比。了解这一情况，有助于在测量非正弦周期电流或电压时恰当地选择和使用不同类型的仪表。

思考题

（1）周期为10 ms方波的基波频率是多少？

（2）确定图4-29所示波形的周期、基波频率。

图4-29　波形

（a）三角波；（b）锯齿波

（3）若基波频率为100 Hz，则2次谐波是多少？

（4）确定非正弦周期电流i（t）=0.2+0.8sin（ωt-15°）+0.3sin（2ωt+40°）A的有效值。

（5）确定非正弦周期电压的有效值。

（6）锯齿波电压u的波形如图4-30所示，如果其幅值Um=100V，计算u的有效值（查表4-1，k=5）。

图4-30　锯齿波形