一阶RC电路的响应分析

一个由直流电源、电阻和电容组成的动态电路如图3-28所示。

图3-28　一阶RC电路响应

在电路中，开关接在位置1已久，电容已被充电，两端电压为U0，即uC（0-）=U0，在t=0时刻，电路换路，开关接在位置2，外施激励直流电压源US加到RC串联电路中，下面来分析电路中的响应uC。

根据KVL可以列出电路的电压方程为

将和代入上式，得

式（3-20）是一阶微分方程，求解uC，得

两边同时积分，得

得到

式中　A——积分常数，其值可由初始条件确定。

根据换路定律，因为uC（0-）=U0，所以当t=0+时，uC（0+）=uC（0-）=U0，代入式（3-21）中，得到

将求得的A再代入式（3-21）得

这就是过渡过程中电容电压uC随时间t的变化规律。

根据图3-28，电阻电压为

电路中的电流为

以下对分析结果做一些讨论。

1.零输入响应

在式（3-22）～式（3-24）中，如果US=0，即电路没有外施电源的输入，这时电路的响应完全是由储能元件的初始储能激励而产生的，这样的响应称为零输入响应。

初始值为

由式（3-22）得此时电容电压为

由式（3-23）得电阻电压为

由式（3-24）得电路中的电流为

零输入响应实质上就是电容的放电过程。电容通过电阻R放电，电容器储存的电能被逐渐释放出来，电容电压、电流、电阻电压逐渐减小，直到零为止。而且在放电过程中电容元件的电压uC、电流iC、电阻电压uR都是随时间按指数函数规律不断衰减，最终趋于零。放电结束后，电路重新达到稳态。它们的波形如图3-29所示。

图3-29　RC一阶电路零输入响应

（a）电容电压和电阻电压变化规律；（b）电容电流变化规律

2.零状态响应

在式（3-22）～式（3-24）中，如果U0=0，RC电路中电容电压uC（0+）=U0=0，即电容事先没有被充电，RC动态电路初始状态为零时，由外加激励信号所引起的响应称为电路的零状态响应。

t→∞时刻的值，表示换路后的电路重新稳定的电压或电流值统称为稳态值。根据图3-28，uC（∞）=US，iC（∞）=0（电容开路），uR（∞）=iC（∞）R=0。

由式（3-22）得电容电压为

由式（3-23）得电阻电压为

由式（3-24）得电路中的电流为

零状态响应实质上就是电容的充电过程。在充电过程中，电容元件的电压uC是随时间从零值按指数函数规律不断上升，最终等于电源电压US；而电阻的电压uR却是从零值跃变到最大值US后按指数函数规律衰减到零；电容的电流i同电阻电压相似，也是从零值跃变到最大值后按指数函数规律衰减到零。充电结束后，电路重新达到稳态。这时电容相当于开路，电路中无电流，电阻自然也就无电压。它们的波形如图3-30所示。

图3-30　RC电路零状态响应

（a）电容电压和电阻电压变化规律；（b）电容电流变化规律(www.xing528.com)

3.全响应

在式（3-22）、式（3-23）、式（3-24）中，如果US≠0，同时U0≠0，这时电路的响应在非零状态的电路中，由外施激励和初始储能共同作用产生的，这样的响应称为全响应。

如果U0＞US，是电容的放电过程；如果U0＜US，则是电容的充电过程；而如果U0=US，则电容既不充电也不放电，这时电路没有过渡过程。这就是电路要产生过渡过程的条件（电容电压、电感电流值不等于新的稳态时的电压、电流值）产生的原因。全响应时电容电压uC的波形如图3-31所示。

图3-31　RC电路全响应电容电压变化规律

（a）U0＞US；（b）U0＜US；（c）U0= US

因为uC（0+）=U0，uC（∞）=US，式（3-28）可写为

4.时间常数

令τ=RC，τ的单位为

由于τ具有时间的单位，故称为时间常数。

时间常数τ的大小决定过渡过程的长短。以零输入响应电容电压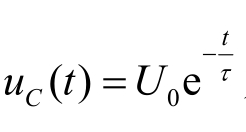为例分析，uC随时间衰减的情况如表3-1所列。

表3-1　电容电压随时间变化的规律

表3-1中的数值说明，t=τ时的值约为初始值的0.368倍，表示放电过程中，电容电压衰减至初始值的0.368倍所需经历的时间等于时间常数τ。这一时间越长，放电进行得越慢；反之，放电进行很快。

从理论上说，t→∞电容电压才衰减至零。实际上，t=5τ时，电容电压已衰减为初始值的0.007倍，可以认为电路已经达到新的稳态。在工程中，一般认为经过（3～5）τ时间，过渡过程基本结束，电路已达到新的稳态。

时间常数τ仅取决于电路的结构和元件参数。它的大小直接影响电路过渡过程的快慢。时间常数τ越大，过渡过程进行得越慢，过渡过程越长。例如，零输入响应电容放电，在U0为定值时，电容C值越大，储能越多，放电时间就越长；电阻R越大，放电电流越小，放电时间也越长；反之，时间常数τ越小，过渡过程进行得越快，过渡过程越短。

引入时间常数后，式（3-31）可以写为

式（3-32）中，uC（0+）≠uC（∞），全响应电容电压uC由两项组成，第一项为常量uC（∞），它是电容电压在电路达到新的稳态时的电压值（也叫稳态值），所以这一项就叫稳态分量。第二项是时间的指数函数，随时间按指数函数规律最终会衰减到零，把这一项叫做暂态分量。所以，过渡过程中的电容电压可以分解为稳态分量与暂态分量之和，即

式（3-33）说明

另外，将式（3-32）可以改写为

式（3-34）中，第一项是零输入响应，第二项是零状态响应。所以过渡过程中的电容电压又可以分解为零输入响应与零状态响应之和，即

式（3-34）说明，一阶电路的全响应等于由电路的初始状态单独作用引起的零输入响应和由外施激励单独作用所引起的零状态响应之和。这正是叠加定理的体现。

实际上全响应无论怎样分解，都是为了分析方便而人为作的分解，电路的实质是，换路前的电路处于一种能量状态，换路后电路又处于另一种能量状态，过渡过程就是电路从一种能量状态向另一种能量状态的转换过程。

例3.7　在图3-28所示电路中，U0=0，US=12 V，R=5 kΩ，C=1 000 μF，开关S闭合前电路处于零状态，t=0时开关闭合，求闭合后的uC（t）和iC（t）。

解

将τ=5s，US=12 V，代入式（3-2），得

例3.8　已知图3-32中的C=10μF，R=2kΩ，电容的初始电能为2×10-3 J，求：① 电路的uC（t）和iC（t）；② 电容电压衰减到8 V时所需时间；③ 要使电压在4 s时衰减到2 V，电阻R取值为多少？

图3-32　例3.8用图

解　① 由电容的储能公式知，所以

时间常数

这是零输入响应，将uC（0+）和τ代入式（3-28）中，得

② uC（t）=8V时，20e-50t=8V，得计算得

③ 由uC（t）=20e-t/RC，得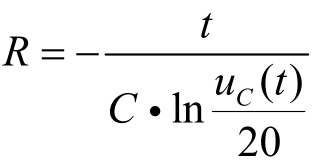

将uC（t）=2V ，C=10μF，t=4 s，代入上式，计算得