控制器参数整定的理论计算与工程实践方法分析

所谓参数整定，就是对一个已经设计并安装就绪的控制系统，选择合适的控制器参数[δ，T_i，T_d]，来改善系统的静态和动态特性，使系统的过渡过程达到最为满意的质量指标要求。控制器参数的整定方法很多，归纳起来可以分为两大类，即理论计算整定法和工程整定法。对于工程整定法，工程技术人员无需确切的知道对象的数学模型，就可以在控制系统中直接进行整定。常用的工程整定法有经验法、临界比例度法、衰减曲线法、响应曲线法。

1.经验法

这种方实质上是一种经验凑试法，是工程技术人员在长期的生产实践中总结出来的一种整定方法。

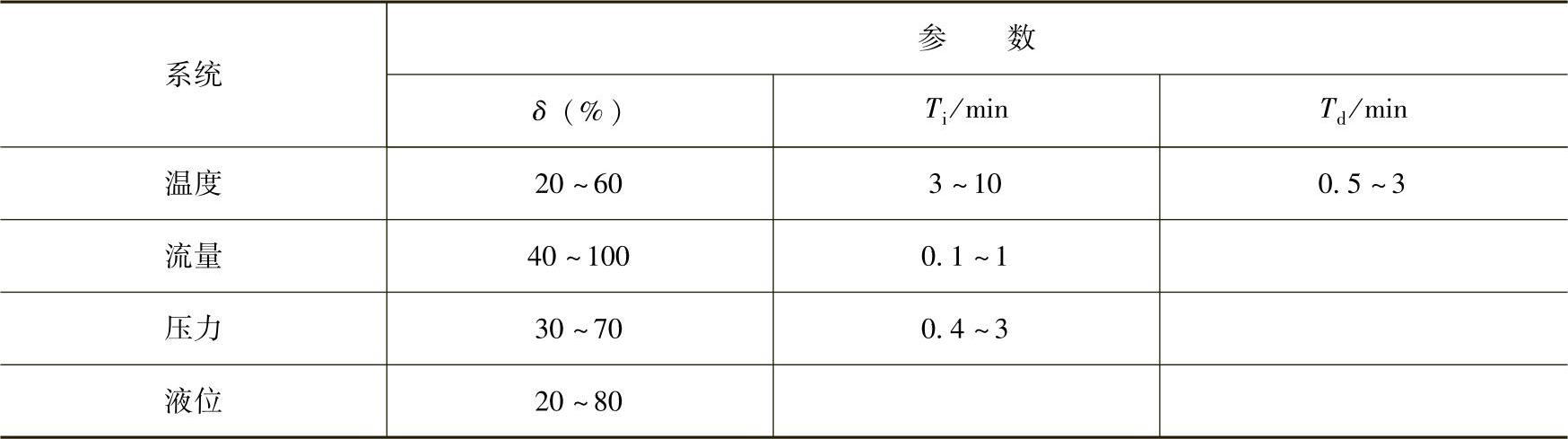
具体整定方法：根据经验先将控制器参数放在某些数值上，直接在闭合的控制系统中通过改变给定值以施加干扰，看输出曲线的形状，以δ%、T_i、T_d，对控制过程的规律为指导，调整相应的参数进行凑试，直到合适为止。控制器参数经验数据见表6-1。

表6-1 控制器参数经验数据

2.临界比例度法

所谓临界比例度法，是在系统闭环的情况下，用纯比例控制的方法获得临界振荡数据，即临界比例度δ_k和临界振荡周期T_k，然后利用一些经验公式，求取满足4∶1衰减振荡过渡过程的控制器参数。其整定计算公式见表6-2所示。

表6-2 临界振荡整定计算公式

具体整定方法如下：(www.xing528.com)

在纯比例作用下，即将T_i放最大，T_d放“0”位置上，在干扰作用下，从大到小调整比例度，直到系统出现等幅振荡（即临界振荡），记下此时的比例度δ_k及振荡周期T_k，然后按表6-2的数值计算出调节器的各整定参数值。

3.响应曲线法（根据广义对象的时间特性来整定参数）

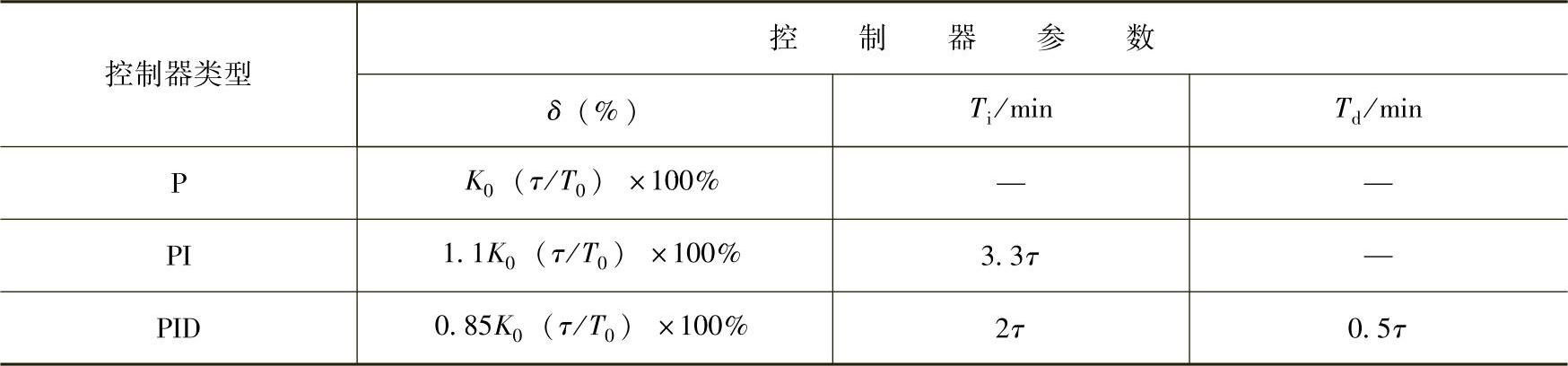
反应曲线法是根据广义对象的时间特性，通过经验公式求取。当操纵变量作阶跃变化时，被控变量随时间的变化曲线称为反应曲线。对自衡的非振荡过程，广义对象的传递函数常用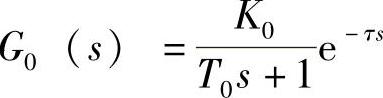来近似，其中K₀、τ和T₀则可由反应曲线用图解法得出。控制器参数整定的反应曲线法是根据广义对象的K₀、τ和T₀确定控制器参数的方法。有了K₀、τ和T₀参数法，就可以根据表6-3中的经验公式，计算出满足4∶1衰减振荡的控制器整定参数。

表6-3 反应曲线法控制器参数计算表（4∶1衰减比）

4.衰减曲线法的工程参数整定

该方法与临界比例度法的整定过程有些相似，方法是：在纯比例作用下，由大到小调整比例度以得到具有衰减比（4∶1）的过渡过程，记下此时的比例度δ_s及振荡周期T_s，根据经验公式，求出相应的积分时间T_i和微分时间T_d，然后根据表6-4中相应的经验公式，求出控制器的整定参数。

表6-4 衰减曲线法控制器参数计算表（4∶1衰减比）