应用事件研究法分析疫情影响

上一节根据历史数据建立的猪肉价格风险预警决策树模型并不能对疫情的影响进行分析，因为历史数据中缺乏疫情影响方面的信息。但由8.2节的数据可知，疫情前后猪肉价格发生大幅波动。为了克服这个缺陷，需要进一步分析疫情对猪肉价格产生什么冲击。如上所述，猪肉价格的影响因素众多，市场价格是多种因素综合作用的结果。那么，如何剔除其他因素，而把握疫情本身给猪肉价格带来怎样的影响呢？在财务金融领域，经常应用事件研究法（Event Study）来定量分析某一特定事件的发生对价格或收益率的影响，以此检验市场对新信息披露的反应程度，并提供了一个指标即累计超常收益率（Cumulative Abnormal Returns，CAR）对反应程度进行度量。事件研究法作为检验市场效率的一种方法，在资本市场研究中起着重要的作用，并被广泛运用于其他相关领域。为此，我们借鉴事件研究法的思想来定量分析疫情对猪肉价格的影响。

8.3.3.1　事件研究法的理论框架

事件研究法依赖三个基本假设：①有效市场假说（Efficient Markets Hypothesis，EMH），即市场是有效的，价格反映所有已知的公共信息；②所研究的事件是市场未预期到的，因此这种超常收益可以衡量价格对事件发生或信息披露异常反应的程度；③在事件发生的窗口期间无其他事件的混合效应。

（1）事件研究法的主要概念

事件日（Event date）：特定事件发生的日期（t＝0）。

事件窗口期（Event window）：对事件涉及的价格进行考察的时间段（［t 1，t 2］，通常t 1＜0且t 2＞0）。例如，研究企业兼并收购等事件对其股票价格的影响时，事件日期就是企业发布并购公告的当天。事件窗口从发布并购公告的当日开始，依据研究目的包含公告发布的前一天和公告发布的后一天。有时候也会包含事件发生的前后数日。

估计窗口（Estimation window）：估计窗口一般选择为事件发生前一段时间，估计窗口与事件窗口无交集。

正常收益（Normal Returns）：为了考察特定事件对价格的影响，首先需要知道，如果没有该事件发生，收益率应该是多少，这也就是需要估计正常收益率的原因。

超常收益率（Abnormal Returns，AR）：实际收益率与正常收益率的差值，超常收益率能够反映该事件的经济影响。

累积超常收益率（Cumulative abnormal returns，CAR）：在事件窗口内超常收益率的简单加总。

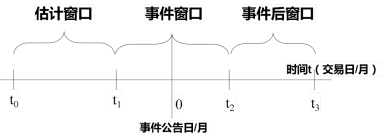
图8.8　事件研究法的窗口期划分

（2）事件研究法的估计模型

如果市场是有效的、某一事件是意料之外的，并且该事件的发生与市场价值相关，那么通过将事后公司实际收益（AR）减去统计模型估计的正常收益率便能得到超常收益率。在进行超常收益率估计之前，首先需要定义事件发生的窗口期。通常，包括事件发生日期当天与事件发生日的前后数天。接着定义估计窗口，并选择估计模型计算预期收益率。

以市场模型（Market Model）估计预期收益率为例，超常收益率（AR）可表示为：

其中Ri，t表示实际收益率，（αi+βiR m，t）表示由超额收益αi、市场性风险βi以及市场收益率Rm，t决定的预期收益率。

包括市场模型在内，预期收益率可由以下五种估计模型进行估计：

市场模型（Market Model）：

资产i在时间t的收益率R i，t可以由该资产与市场收益率Rm，t的回归模型得到。比如某公司的股价跟大盘指数或行业指数存在某种相关性，可以根据估计窗口期中的公司股价和大盘指数等数据建立线性回归方程，在事件窗口期中则可以基于该回归方程，利用大盘指数（或行业指数）来计算该公司股票的预期正常收益率。

市场调整模型（Market-adjused Model）：

Fama三因素模型（Fama-French Three Factor Model）：

其中Rf，t表示时间t的无风险收益率；Rm，t表示时间t的市场收益率；Ri，t表示资产i在时间t的收益率；［Rm，t-Rf，t］是市场风险溢价，SMBt为时间t的市值（Size）因子的模拟组合收益率（Small minus Big），HMLt为时间t的账面市值比（book-to-market）因子的模拟组合收益率（High minus Low）。

Carhart四因素模型（Fama-French Plus Momentum）：

Carhart四因素模型是在Fama三因素模型的基础上，通过引入动量因素而构造的四因素模型，对于绩效的解释能力有了很大的提高。四因素模型将收益表示为在市场因素（MKT）、规模因素（SMB）、价值因素（HML）与动量因素（MOM）共同作用下所达到的一个均衡。其中MOMt表示t时刻的动量因子，在模型中新加入的动量因素能够对市场上的“趋势效应”进行有效解释。

历史平均模型（HMM），即事件窗口期的正常收益率使用估计窗口的期望值代替：

（3）事件研究法的估计步骤

1）定义事件与事件窗口

通常可以将事件分为以下三种：有关公司活动的公告；有关宏观经济事件的公告；来自政府监管与政策层面的公告。事件窗口期为包含事件日的一段时间。

2）数据准备：合并事件数据

定义好事件发生的日期与事件窗口期后，需要进行事件研究的数据准备，一般包括历史收益率数据以及事件发生的日期数据。

3）估计正常收益率与计算超常收益率

如前所述，可以使用五种估计模型计算正常收益率，以最常见的市场模型（Market model）为例，Ri，t为公司i在第t天的收益率，Rm，t是市场在第t天的收益率，应用最小二乘法OLS回归：

得到估计系数后，可使用以下公式计算超常收益率：

在使用市场调整模型（Market-adjusted model）估计正常收益率时，模型设定为αi＝0与βi＝1。同理，使用其他两种估计模型计算正常收益率的方法也相似，只不过在OLS回归的时候将单个公司收益率与市场收益率同时减去无风险利率Rf，t分别作为因变量和主要的自变量进行估计，并加入更多定价因子SMBt和HML t以及MOM t作控制变量。

4）计算超常收益率并加总超常收益率（CAR）

AR i，t计算的是公司i在第t天的超常收益率，为了研究事件对整体资产价格的影响，还需要计算平均超常收益率AA R i，t和累积超常收益率CA R i，t。通常而言，平均超常收益率是针对某一时点、对所有公司的超常收益率求平均，计算方式如下所示：

其中，t为事件窗口期的某时间，N为公司个数。累积超常收益率是计算公司i在t 1到t 2某一段时期内，平均超常收益率的总和，计算方式如如下所示：

在此基础上，计算平均累积超常收益率，也即在特定时点t，对所有公司的累计超常收益率求平均，计算方式如下所示：

以上公式中，t 1和t 2是之前已经定义好的事件窗口的左右两端。

5）检验CAR的显著性

计算出累积超常收益率之后，最后需要检验累积超常收益是否在统计上异于零，以便判断事件的发生是否对价格产生了显著的影响。

8.3.3.2　基于ARIMA的无疫情市场模型

上述事件研究法的计算步骤的关键是第3步，即建立市场模型，估计事件不发生情况下的正常收益率，在此基础上将实际收益率与正常收益率相减，得到的超常收益率就是由该事件所带来的影响。收益率通常表示为第t期的资产价格减去第（t-1）期的价格再除以第（t-1）期的价格。因此估计正常收益率的问题实际上就是估计在事件不发生时的预期价格。事件研究法根据市场模型来预测事件窗口期的资产价格，其思想基于有效市场假设，特别是资本市场。市场价格比较容易确定，比如依据大盘指数可以估计事件窗口期的正常收益率。猪肉虽然也和肉食品市场有关，但是却很难用一个比较好的市场指数来表示市场价格。并且如前所述，影响猪肉价格的影响因素很多，因此建立市场因素回归模型是困难的。但猪肉价格却往往具有较好的时间特征，如季节性、周期性等，因此为了确定事件期内的无疫情影响的正常价格，我们可以使用时间序列方法进行预测。一旦计算得出了无疫情正常价格，再用疫情事件期内的实际价格减去无疫情正常价格，就可以得到疫情对猪肉价格的影响程度。时间序列分析是计量经济学的重要内容，有很多时间序列分析方法，如移动平均法、指数平滑法、趋势分析法、季节指数法、Holt-Winter预测法以及自回归差分移动平均法（Auto-Regressive Integrated Moving Average，ARIMA），甚至当前的人工智能领域有一些深度神经网络的机器学习方法，如循环神经网络（Recurrent Neural Network，RNN）、长短期记忆网络（Long short-term memory，LSTM）均可用于时间序列预测。这些方法各有特点及适用场景，其中ARl MA模型在经济预测过程中由于既考虑了经济现象在时间序列上的依存性，又考虑了随机波动的干扰性，还能处理季节性问题，预测准确率较高，是近年应用比较广泛的方法之一。因此，本文采用ARIMA模型来对无疫情影响的猪肉正常价格进行预测。

（1）ARIMA模型的基本原理

ARIMA模型全称为差分自回归移动平均模型。是由博克思和詹金斯于20世纪70年代初提出的一著名时间序列预测方法。其中ARIMA（p，d，q）称为差分自回归移动平均模型，AR是自回归，p为自回归项；MA为移动平均，q为移动平均项数，d为时间序列变为平稳时所做的差分次数。

ARIMA模型的基本思想是：将预测对象随时间推移而形成的数据序列视为一个随机序列，用一定的数学模型来近似描述这个序列。这个模型一旦被识别后就可以根据时间序列的过去值及现在值去预测未来值。

（2）时间序列的AR、MA和ARIMA建模

1）自回归过程(www.xing528.com)

令Y t表示t时期的数据。如果我们把Y t的模型写成

其中δ是Y的均值，而u t是具有零均值和恒定方差σ2的不相关随机误差项（即u t是白噪音），则Y t遵循一个一阶自回归或AR（1）随机过程。

P阶自回归函数形式写成：

模型中只有Y这一个变量，没有其他变量。

2）移动平均过程

上述AR过程并非是产生Y的唯一可能机制。如果Y的模型描述成

其中μ是常数，u为白噪音（零均值、恒定方差、非自相关）随机误差项。t时期的Y等于一个常数加上现在和过去误差项的一个移动平均值。则称Y遵循一个一阶移动平均或MA（1）过程。

q阶移动平均可以写成：

3）自回归与移动平均过程

如果Y兼有AR和MA的特性，则是ARMA过程。Y可以写成

其中有一个自回归项和一个移动平均项，那么它就是一个ARMA（1，1）过程。Θ是常数项。

ARMA（p，q）过程中有p个自回归和q个移动平均项。

4）自回归整合移动平均过程

上面所做的都是基于数据是平稳的，但是很多时候时间数据是非平稳的，即是单整（单积）的，一般非平稳数据经过差分可以得到平稳数据。因此如果我们讲一个时间序列差分d次，变成平稳的，然后用ARMA（p，q）模型，则我们就说那个原始的时间序列是ARIMA（p，d，q），即自回归差分移动平均时间序列。ARIMA（p，0，q）＝ARMA（p，q）。

（3）基本思路和基本程序

1）基本思路

步骤一：识别。找出适当的p、d和q值。通过相关图和偏相关图可以解决。

步骤二：估计。估计模型所含自回归和移动平均项的参数。有时可以用最小二乘法，有时候需要用非线性估计方法。

步骤三：诊断（检验）。看计算出来的残差是不是白噪音。是，则接受拟合；不是，则重新再做。

步骤四：预测。短期更为可靠。

2）基本程序

第一步，根据时间序列的散点图、自相关函数和偏自相关函数图以ADF单位根检验其方差、趋势及其季节性变化规律，对序列的平稳性进行识别。一般来讲，经济运行的时间序列都不是平稳序列。

第二步，对非平稳序列进行平稳化处理。如果数据序列是非平稳的，并存在一定的增长或下降趋势，则需要对数据进行差分处理。如果数据存在异方差，则需对数据进行技术处理，直到处理后的数据的自相关函数值和偏相关函数值无显著地异于零。

第三步，根据时间序列模型的识别规则，建立相应的模型。若平稳序列的偏相关函数是截尾的，而自相关函数是拖尾的，可断定序列适合AR模型；若平稳序列的偏相关函数是拖尾的，而自相关函数是截尾的，则可断定序列适合MA模型；若平稳序列的偏相关函数和自相关函数均是拖尾的，则序列适合ARMA模型。

可以通过观察相关图中的自相关函数（ACF）和偏相关函数（PACF）得出数据适用于AR、MA还是ARIMA模型，并通过图形形状来判断p，d，q。

表8.14　ACF与PACF的理论模式

注：指数衰减和几何衰减意义相同。

（1）p阶自回归模型AR（p）

AR（p）模型的偏自相关函数PACF在p阶之后应为零，称其具有截尾性；

AR（p）模型的自相关函数ACF不能在某一步之后为零（截尾），而是按指数衰减（或成正弦波形式），称其具有拖尾性。

（2）q阶移动平均模型MA（q）

MA（q）模型的自相关函数ACF在q阶之后应为零，称其具有截尾性；

MA（q）模型的偏自相关函数PACF不能在某一步之后为零（截尾），而是按指数衰减（或成正弦波形式），称其具有拖尾性。

第四步，进行参数估计，检验是否具有统计意义。

第五步，进行假设检验，诊断残差序列是否为白噪声。

第六步，利用已通过检验的模型进行预测分析。

（4）无疫情影响的猪肉正常价格预测

ARIMA通过设定好3个参数，能够在一个模型中同时处理包含趋势性、季节性和不规则性的多种时间序列成分，是一种重要的预测方法。本文试图以ARIMA时间序列分析方法来建立生猪和玉米价格的预测模型。

用ARIMA模型进行预测，最关键的是确定3个模型参数（p，d，q），其中p是ARIMA模型中的自回归项数，q是方程中包含的移动平均项数，d是为了使时间序列变成平稳序列需要进行的差分次数（又称为差分阶数）。利用ARIMA模型进行预测的时候，一般先画出时间序列的散点图，计算自相关函数和偏自相关函数，结合ADF单位根检验序列的平稳性、趋势性和其季节性变化规律。对于有趋势成分的时间序列，可以先对数据进行差分处理［158，159］。在R语言中可以通过调用auto.arima（）方法辅助确定最优p，d，q参数。

我们编写了R语言程序，基于2010—2020年10余年的猪肉、玉米月度数据，使用ARIMA模型对2018年8月疫情发生以后的24期数据进行预测。如下：

表8.15　基于ARIMA模型的猪肉价格预测R程序代码

预测结果如下图所示：

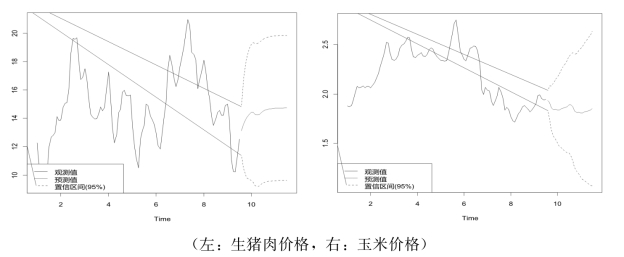
图8.9　基于ARIMA模型的价格预测

我们通过auto.arima（ts＿pork＿price，trace＝TRUE）确定p，d，q参数，得到最优模型为fit＜-arima（ts＿pork＿price，order＝c（2，0，2），list（order＝c（0，0，1），period＝12）），还需要进行模型的检验（玉米价格最优模型参数是：ARIMA（0，1，1）（1，0，1）［12］）。在R语言中，Tsdiag方法用来对时间序列模型进行综合分析诊断，可以给出标准残差的序列图、残差的样本ACF和Ljung-Box检验统计量的p值。如果模型是适当的，其残差自相关性应近似无关，服从均值为0、方差为1/n的正态分布。我们的模型检验结果如下图所示。由图可知，对于猪肉和玉米价格预测的两个ARIMA模型，其残差在0附近波动，残差的自相关系数均接近于0。Ljung-Box检验是根据滞后阶数来检验时间序列是否存在自相关性以及随机独立性。如果观测值相互之间不独立，则观测值会在i个时间单位后和其他观测值相关，呈现自相关关系，进而降低ARIMA模型预测的准确性。p值在虚线（5%）上方则表明没有证据来拒绝误差项是不相关的零假设，即只能接受数据的独立性假设。我们的模型其p值均远大于0.05，因此可以认为残差是高斯白噪声序列，该ARIMA模型较为合适。

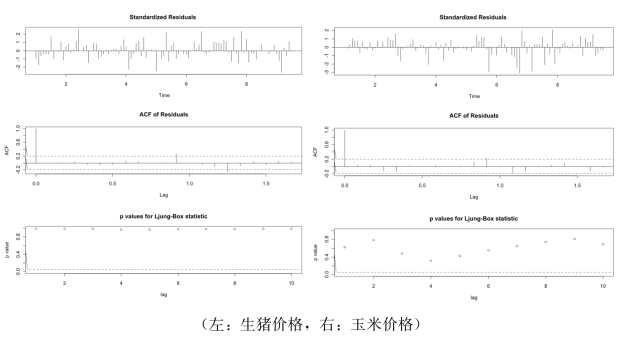
图8.10　ARIMA预测模型的检验

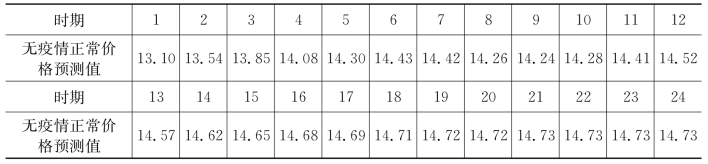
基于ARIMA模型的无疫情影响的猪肉正常价格预测值如表8.16所示。可见如果不发生疫情，2018年8月以后的猪肉价格会有所上升，但最大值仅为14.73元/kg，甚至低于疫情前2010.1—2018.7期间的平均值14.88元/kg（见表8.7），但实际上，在疫情的影响下，2018.8—2020.6期间猪肉平均价格为23.66元/kg，最高价达到了37.88元/kg，远高于无疫情影响下预测值中的最高价14.73元/kg。由此可见，猪瘟疫情对猪肉价格产生的巨大的冲击，使得猪肉价格产生了大幅的上涨。

表8.16　无疫情影响的正常价格预测值

接下来，我们完成事件研究法的后续步骤，进一步分析疫情影响的具体程度。