猪肉价格预警的主要内容是建立一个预测模型,分析各种因素对猪肉价格风险等级的影响情况,根据历史数据构建一系列决策规则,并预测在什么情形下会出现哪一类风险。在此基础上,通过不断对影响因素指标(自变量)的数据采集,依据建立起来的决策规则,预测可能引发的风险等级(因变量),从而对猪肉价格风险起到预警的作用。
因此,风险预警的关键是建立猪肉价格风险的预测模型。如前所述,因变量猪肉价格风险等级可以分为5类,即负向高度风险、负向一般风险、无风险、正向一般风险、正向高度风险。对于因变量为离散型数据的预测问题,可以使用数据挖掘中的分类模型加以解决。分类模型有很多,如决策树、贝叶斯、人工神经网络、K-近邻、支持向量机、Logistic回归等,这些方法各有特点。而分类回归树CART(Classification And Regression Tree)模型是一种非常基础而重要的决策树模型,它对决策规则的解释性强,应用非常广泛。我们采用CART算法来构建猪肉价格的风险预警决策模型。
8.3.2.1 CART分类回归树算法介绍
决策树是以实例为基础的归纳学习算法,它能够从一组无序、无规则的实例中推理出以决策树表示的分类规则。主要的决策树算法有ID3、C4.5(C5.0)、CART及RF(Random Forest)、GBDT(Gradient Boosting Decision Tree)等。决策树方法不仅能得出决策规则,结果直观,解释性强,特别是大数据时代,训练样本的增加还能提高模型的准确性,因此受到业界重视。
分类回归树算法:CART算法采用一种二分递归分割的技术,将当前的样本集分为两个子样本集,使得生成的的每个非叶子节点都有两个分支。因此,CART算法生成的决策树是结构简洁的二叉树。
分类树两个基本思想:第一个是将训练样本进行递归地划分自变量空间来构建决策树,第二个是用验证数据进行剪枝。
建树:在分类回归树中,把类别集Result表示为因变量,选取的属性集表示为自变量,通过递归的方式把属性集p维空间划分为不重叠的矩形。它检查每个变量和该变量所有可能的划分值来发现最好的划分,对离散值如{x,y,z},则在该属性上的划分有三种情况({{x,y},{z}},{{x,z},y},{{y,z},x}),空集和全集的划分除外;对于连续值处理引进“分裂点”的思想,假设样本集中某个属性共n个连续值,则有n-1个分裂点,每个“分裂点”为相邻两个连续值的均值(a[i]+a[i+1])/2。将每个属性的所有划分按照他们能减少的杂质(合成物中的异质、不同成分)量来进行排序,杂质的减少被定义为划分前的杂质减去划分之后每个节点的杂质量*划分所占样本比率之和,目前最流行的杂质度量方法是GINI指标,如果用k,k=1,2,3……C表示类,其中C是类别集Result的因变量数目,一个节点A的GINI不纯度定义为:
![]()
其中,p k表示观测点中属于k类的概率,当Gini(A)=0时所有样本属于同一类,当所有类在节点中以相同的概率出现时,Gini(A)最大化,此时值为(C-1)C/2。
对于分类回归树,A如果它不满足“T都属于同一类别或T中只剩下一个样本”,则此节点为非叶节点,所以尝试根据样本的每一个属性及可能的属性值,对样本进行二元划分,假设分类后A分为B和C,其中B占A中样本的比例为p,C为q(显然p+q=1)。则杂质改变量:Gini(A)-p*Gini(B)-q*Gini(C),每次划分该值应为非负,只有这样划分才有意义,对每个属性值尝试划分的目的就是找到杂质该变量最大的一个划分,该属性值划分的子树即为最优分支。
剪枝:在CART过程中第二个关键的思想是用独立的验证数据集对训练集生长的树进行剪枝。
分析分类回归树的递归建树过程,不难发现它实质上存在着一个数据过度拟合问题。在决策树构造时,由于训练数据中的噪音或孤立点,许多分枝反映的是训练数据中的异常,使用这样的判定树对类别未知的数据进行分类,分类的准确性不高。因此应减去这些分支的过程被称为树剪枝。树剪枝方法用于处理过分适应数据问题。通常,这种方法使用统计度量,减去最不可靠的分支,这将导致较快的分类,提高树独立于训练数据正确分类的能力。
决策树常用的剪枝方法有两种:事前剪枝和事后剪枝。CART算法经常采用事后剪枝方法,该方法是通过在完全生长的树上剪去分枝实现的,通过删除节点的分支来剪去树节点。最下面未被剪枝的节点成为树叶。
CART用的成本复杂性标准是分类树的简单误分(基于验证数据的)加上一个对树的大小的惩罚因素。惩罚因素是有参数的,用a表示每个节点的惩罚。成本复杂性标准对于一个数来说是Err(T)+a|L(T)|,其中Err(T)是验证数据被树误分部分,L(T)是树T的叶节点树,a是每个节点的惩罚成本:一个从0向上变动的数字。当a=0时对树有太多的节点没有惩罚,用的成本复杂性标准是完全生长的没有剪枝的树。在剪枝形成的一系列树中,从其中选择一个在验证数据集上具有最小误分的树作为最后的决策树。
8.3.2.2 用CART算法建立猪肉价格预警决策模型
(1)输入变量的选择
如前所述,影响猪肉价格的因素众多,涉及供求关系、生产成本、宏观经济环境、猪肉进口、汇率等,我们试图建立猪肉价格风险决策模型。我们为每个数据样本定义一个“风险等级”(Riskvalue)标签,分别取“负向高度风险、负向一般风险、无风险、正向一般风险、正向高度风险”等值。因此该价格预警决策问题转化为一个因变量取值为上述离散值的分类问题。
输入变量是模型中的自变量,在建模过程中需要寻找自变量与目标变量的关联。基于前面的讨论,模型自变量选取了9个,为:meatprice(生猪价格)、cornprice(玉米价格)、consumerlevel(居民消费水平:元)、beanmeal(豆粕均价)、meatvolume(猪肉产量-万吨)、currencyratio(美元汇率)、meatimport(猪肉进口量-万吨)、CPI(CPI同比增长)、GDPgrowth(GDP增速)。我们采集了近10年(2010—2019年)每个月的上述指标数据,构建CART决策树模型,并用R语言作了实现,程序源代码如下表所示:
表8.10 基于CART模型的猪肉价格预警R程序代码
 (https://www.xing528.com)
(https://www.xing528.com)

(2)决策树模型结果解释与应用
首先,对120个样本,按(0.7,0.3)的概率抽样得到训练样本83个,测试样本37个,得到决策变量与食品风险等级的树状决策图。图8.6中不同颜色的矩形分别代表了不同的风险等级,绿色为无风险,红色为负向高度风险。
由图可见,从10年来的历史数据来看,猪肉价格总体而言为“无风险”状态,CART模型建立的决策规则首先选择猪肉价格为决策变量,meatprice=15为分割点,当meatprice<15时(决策树的左侧分枝),猪肉价格出现负向风险的可能性比较大,而在决策树的左侧(meatprice≥15),猪肉价格出现无风险或正向的风险的可能性较大。这符合我们的直觉判断。但猪肉价格15元/kg的分割点是从历史数据中机器学习的结果。此外,当产生第一个分支后,算法会继续作变量的选择,比如后续会将玉米价格(cornprice)和消费水平(consumerlevel)作为新的分割变量,不断递归和剪枝,生成一棵完整的决策树。
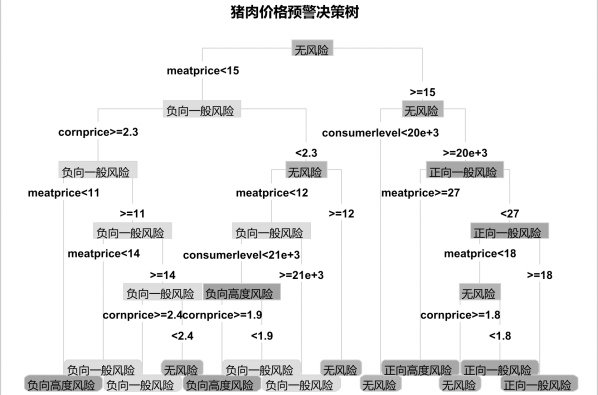
图8.6 猪肉价格预警决策树模型
模型给出的对应决策规则如表8.11所示。每一行是一条规则,给出的信息包括split(分割条件)、n(节点数)、loss(分类错误节点数)、yval(当前分支所属的类别)、yprob(该分支节点取各个类别值的概率)。以第2条规则为例:“2)meatprice<15.02875 48 23负向一般风险(0.062 0.52 0.42 0 0)”,其含义为:在猪肉价格小于15.03时,有48个节点满足该条件,这些节点整体而言可以划入“负向一般风险类别”,但其中有23个节点并不属于“负向一般风险”类,这48个节点取“负向高度风险”“负向一般风险”“无风险”“正向一般风险”“正向高度风险”的概率分别为0.062、0.52、0.42、0、0,即主要以“负向一般风险”和“无风险”为主。
表8.11 猪肉价格价格预警决策规则

(3)模型准确性评价
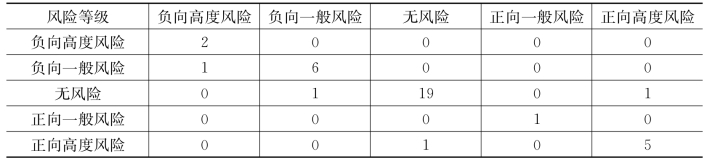
用测试集对模型进行检验,得到的准确性评价矩阵如表8.12所示。每一列表示真实类别,每一行表示预测类别。以第2行为例,CART决策树模型预测的结果为“负向一般风险”,但测试集的真实类别为“负向一般风险”6例,“负向高度风险”1例,可见模型判对6例,判错1例。整体的准确度为(2+6+19+1+5)/37=89.2%,由此可见,决策模型判断准确性是比较高的。
表8.12 准确性矩阵
(4)变量重要性
运用CART模型对决策变量的重要性进行排序,如图8.7所示。变量重要性是指预测变量在决策树所有节点中作为主分支变量(或候选分支变量)时,对分类质量提升程度的总和,因此变量重要性顺序并不一定跟决策树分支变量的出现顺序一致。标准化的变量重要性(Normalized Variable Importance)是将重要性得分最高的变量视为100%,其他变量为该变量与具有最大重要性的变量相除得到的相对百分数。变量重要性反映的是属性变量对目标变量分类的作用。由图可见,生猪价格与玉米价格综合决定了风险等级,而居民消费水平、年猪肉年供应量、GDP和CPI的重要性相对偏小。
表8.13 决策树模型变量相对重要性
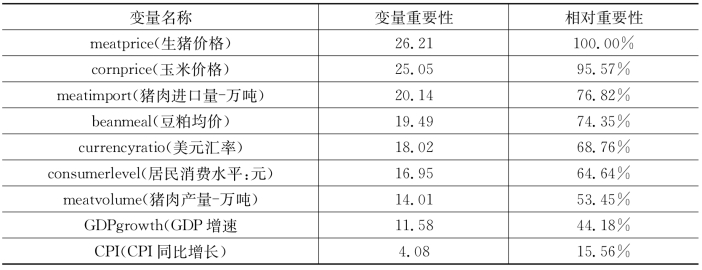
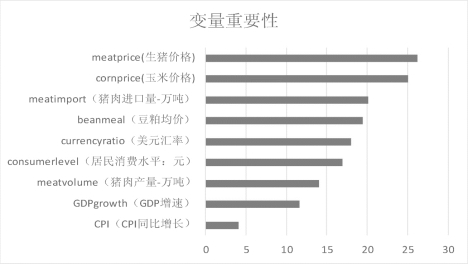
图8.7 猪肉价格预警决策模型变量重要性
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




