面向大数据环境的追溯网络社群识别技术

多数社群识别算法是全局性算法，即将节点和连接的数据全部读入内存以构建网络结构图。如果网络节点数量非常多，这种方法容易造成内存溢出，得不到结果，或者不断在内存和硬盘之间交换数据，时间与复杂度增加，性能下降。为提高计算能力，应对大规模网络场景，用分布式计算架构实现社群识别算法非常必要［129］。

6.3.3.1　正则化马尔科夫聚类算法RMCL

正则化马尔科夫聚类算法是建立在Markov clustering算法基础之上的。假设网络G所对应的图邻接矩阵是A，若G无向无权，则A是一个对称矩阵。可以由A得到图G的标准转移概率矩阵，记为M G，用M（i，j）来表示节点v i到节点v j的转移概率，并且每列之和等于1。矩阵的第i行表示到达节点i的随机游走，第j列表示从节点j开始的随机游走。A和M G之间的关系如下：

D是一个对角矩阵，对角线元素取值如下：

A与M G之间关系记为：M G＝AD-1。

与MCL类似，正则化马尔科夫聚类算法先计算出转移概率矩阵M，再对M不断交替执行扩展、膨胀两个步骤，反复迭代，直到收敛或者变化小于某给定阈值为止。但正则化马尔科夫聚类算法的扩展操作中，对M矩阵的更新过程有所调整。在马尔科夫聚类算法基础上，转移概率矩阵交替进行扩张和膨胀，扩张过程把随机行走传播到新节点，对于有多条路径可达的节点，行走概率更大。相对于不同社群的两节点，同一社群内，由于节点之间路径更多，因此扩张算子会增强同一社群内部节点之间的行走。膨胀操作则可以使得联系紧密的节点之间的联系更加紧密，联系稀疏的节点之间的关系更加疏远。RMCL社群识别的主要步聚如下：

（1）根据网络结构初始化矩阵。对角矩阵为I，I（i，i）＝1，通过A：＝A+I操作把邻接矩阵A对角线上的元素都设成1，这样使得节点随机行走也有可能回到节点自身。M＝M G＝（A+I）D-1。

（2）进行扩展（Expansion）运算。M＝expand（M）＝M*M G，矩阵M中，第i列表示从节点v i到所有其他节点的2步转移概率，M G为标准化初始转移矩阵。正则化马尔科夫聚类算法用Regularized（M）：＝M*M G操作替代了MCL算法的M：＝M*M操作。

（3）进行膨胀（inflation）运算。给定M和参数r，得M inf：

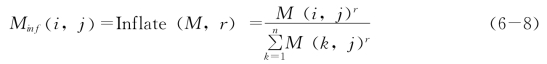
其中r是膨胀参数，其取值通常设为2。为了使节点之间的联系强者更强、弱者更弱，对矩阵中的每个元素概率值都作r次方计算，由于概率值都是小于1的数，作乘方以后，小的概率值将衰减得更加厉害，最后再作一个标准化处理，即让r次方以后的每个元素值除以整列元素之和，结果使得M inf矩阵每列元素之和仍然为1。

（4）进行修剪（Prune）操作。将每列中接近零值的元素移除，加快收敛速度。

（5）判断是否收敛。将本轮M矩阵和上一轮M矩阵进行比较，检查是否发生了显著变化。如果变化小于预先设定的阈值，则表明达到收敛状态，退出迭代结束运算。

（6）完成社群划分，根据M矩阵的最后取值，得到社群划分结果。

6.3.3.2　大规模网络RMCL算法的MapReduce实现

大数据场景下的分布式计算架构当前主要有Map Reduce和总体同步并行计算BSP（Bulk synchronous parallel）两种。Map Reduce架构将复杂的计算任务拆分成两个简单函数Map和Reduce来实现。通过先分解后归约的过程来实现数据和任务的分布式并行处理。

总体同步并行计算架构则采用计算、通信、同步的并行计算模式［141］。基于BSP架构，Google实现了分布式图计算框架Pregel［142］，可以快速进行PageRank中心度、最短路径查找、计算图遍历等操作。然而BSP架构基于消息通信、效率不高、容错性问题也没有得到很好解决［143］。

近年来快速发展的内存计算正逐渐成为分布式计算的主流，比如Berkeley实验室基于Spark开发实现了GraphX图计算接口，并行实现了图分析、图聚类等基础算法［144］，不过目前Graph X支持的社群识别算法还不够丰富。

在开源领域，Hadoop是比较经典的分布式计算平台，目前在很多大数据环境下得到了广泛的应用。它基于MapReduce，具有良好的可伸缩性和稳定性。不过Hadoop的计算能力虽然很强，但是计算效率还有待提升。为了解决大规模食品供应网络的社群识别问题，我们构建了Hadoop大数据集群平台，基于MapReduce实现了正则化马尔科夫聚类算法，说明如下。

我们在Hadoop平台上实现的RMCL算法包括预处理、迭代和后处理3个步骤。在预处理阶段，根据节点的连边情况生成邻居节点列表，表示成为马尔科夫稀疏矩阵，同时，令对角线元素取值都设为1，表明节点除了随机游走到其他节点以外，还可以选择回到自身节点。接着，用每个矩阵元素值除以所在列的非零节点数之和，得到节点权重；迭代步骤扩展Expansion、膨胀Inflation和收敛判断等运算以后，将产生新的转移矩阵，将其与上次结果进行比较。如果没有变化，或变化低于参数预先给定的阈值，或迭代次数达到最大计算次数，运算结束。在后处理阶段主要是根据转移矩阵析出各节点所属社群号，即转移矩阵中节点所在列向量的最大元素下标。RMCL的算法逻辑如下图所示：(www.xing528.com)

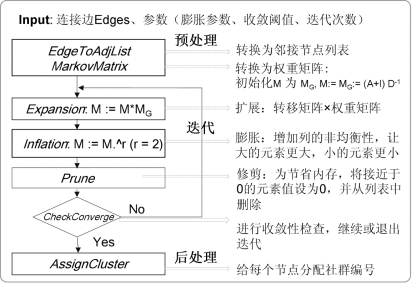
图6.13　RMCL算法逻辑

关于其中的Expansion（扩展）、Inflation（膨胀）和收敛判断运算的MapReduce具体实现，算法如下：

算法1.Expansion（扩展）

Expansion算法的一个最主要的任务就是对大矩阵作乘法运算。对于大规模网络，矩阵的乘法运算资源消耗非常大。为了降低计算开销，设计矩阵乘法运算程序时，通常采用行矩阵、稠密矩阵、索引行矩阵（Indexed Row Matrix）、坐标矩阵（Coordinate Matrix）和分块矩阵（Block Matrix）等不同数据结构，各种结构其实现算法各有不同，性能相差也很大。食品供应链网络通常网络密度比较低，可将邻接矩阵用稀疏矩阵的数据结构来表示，其编码规则为List｛v，Transi（u，v）｝，比如：对于节点u＝18，包含自身在内共有4个节点，记为Adjacent：（u，v）→｛18，252，1，212｝，其转移矩阵为Transi：（u，v）→｛0.25，0.25，0.25，0.25｝，可将稀疏行矩阵编码成｛18：（18 0.25），（252 0.25），（1 0.25），（212 0.25）：4｝的形式。这样，既节省了存储空间，也降低了数据通信量。为了将转移矩阵和权重矩阵区别开来，我们在map过程中，让发送的每个value开头都以“T”或“W”标示，用来代表是转移（Transit）矩阵还是权重（Weight）矩阵。这样可以保证在reduce阶段选择正确的元素进行相乘和累加。此外，在Map阶段，每个列向量元素都会以（i，k）的形式设置成为关键字key并同时发送n份，最终，在Reduce阶段，所有相同的（i，k）都能被第i行和第k列每个元素值获取，进而得到新的转移矩阵，其各元素取值为

算法2.Inflation（膨胀）

Inflation（膨胀）操作将转移矩阵列向量中的各个元素都进行r次方运算，然后作标准化处理，即将各元素值都除以整列元素之和，这样可以保证矩阵每列之和仍为1。由于转移矩阵的元素均是大于0小于1的数，因此，经过r次方运算，越接近0的数衰减越快，越接近于1则衰减越慢。由此可见，经过Inflation运算处理以后，大元素变得更大，小元素变得更小，即拉大了节点之间的差距，使节点之间密者愈密、稀者愈稀。为提高算法的计算效率，加快收敛，还可以对中间数据进行修剪操作，即可以令低于某阈值的元素取值为0并从中删除，从而减少下一轮迭代运算中Expansion算子的计算量。

算法3.Converge Check（收敛判断）

收敛判断是为了提高计算效率，提前完成社群划分的过程而将当前一轮的转移矩阵和上一轮的迭代结果进行比较，若变化值低于预先设定的阈值，或迭代次数达到规定上限，则结束迭代。这里迭代结果比较的是矩阵相似度。测量相似度指标的方法有很多，比较常见的有欧氏Euclidean距离、杰卡德Jaccard相似度、夹角余弦等多种方法。欧氏Euclidean距离法是最常用的方法。其计算公式为对于2个m×n矩阵M x和M y，其距离可以用列向量距离的平均数来表示，（X j，Yj）/n。算法3先在map阶段计算列向量欧氏距离，reduce阶段再将欧氏距离平均，如果小于给定阈值，计算完成。RMCL算法的详细Mapreduce实现代码详见附录5。我们的运算结果表明，即使收敛阈值设置得非常小，经过10～100次迭代，转移矩阵变化值仍可达到收敛，因此，关于阈值选择不须严格设置。

6.3.3.2　基于RMCL算法的社群划分结果

我们构建了Hadoop集群，使用上述算法，对根据德国联邦风险评估研究所提供的食品供应链数据构建的社会网络进行了社群划分，划分结果会对每个网络节点都赋予一个社群号。我们使用Pajek软件对社群划分结果进行可视化展现，不同的社群分别用不同的颜色来表示，节点分布如下图所示。该网络被划分为32个社群，最大的社群是Station 267节点所在群，包含32个节点，约13%的食品工作站属于该社群；最小的社群只有2个成员节点。约80%以上节点（207个）所属的社群其节点数量超过5个，约有12%（33个）的节点其社群规模在2个以下。结合食品供应网络数据，综合比较图6.8和图6.14，可以发现：（1）图6.8中的复杂网络进行社群识别和划分以后，在图6.14中网络结构变得更加清晰。并且，相同的社群内部，节点之间联系紧密，而属于不同社群中的节点之间的联系则很少。表明我们的社群识别算法是有效的。（2）该算法还能够非常清晰地识别出各个社群的中心节点（如果存在的话），即网络往往以度中心性较大的节点为核心进行社群划分，并且社群之间的边界非常明显。也就是说，食品供应网络会在核心节点周围形成社群，这既印证了我们的直觉判断，也对食品供应网络的风险传播范围及关键节点的识别提供了新的技术手段。

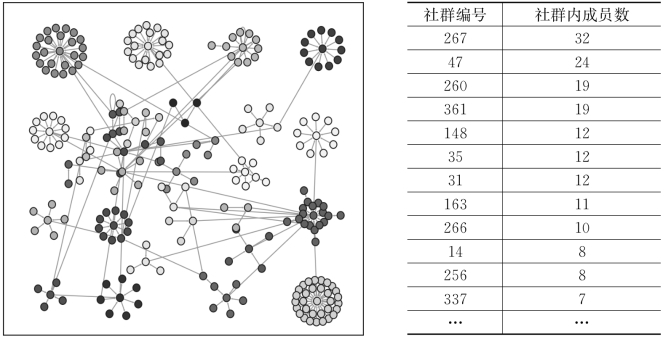
图6.14　食品供应网络社群结构

除了对食品供应网络数据进行社群识别与划分以外，为进一步检验和比较算法性能，我们还对斯坦福大学SNAP提供的2个开放社会网络数据集进行了计算，性能比较如表6.8所示。对于包含3 774 768个节点、16 518 948条连接边的专利引用网络，程序也可以在1 343.802秒内返回结果。通常，程序响应时间与网络规模有关，网络节点越多，结构越复杂，计算量也越大，进行社群识别计算所花费的时间就越长。实验表明，程序运行时间没有随网络规模的增长而非线性增加，均能在有限的时间内返回计算结果，表明我们的算法是有效的。为进一步提高计算性能，今后我们拟深入研究RMCL算法在Spark上的设计和实现。

表6.8　社交网络社群划分执行性能比较

网络数据来源：http://snap.stanford.edu/data（Citation-Patents是美国专利引用的网络数据；Web-Google是谷歌的网页链接数据）