基于贝叶斯推断的风险源估计方法

我们的目标是基于观察列表Θ找到最“可能”的源s*∈V Q。给定观察及其在s*上的先验分布，我们引入一个贝叶斯公式表示源节点s是真实源s*的概率：

为了确定来源，设计一个评价指标选择可行源节点s，使得概率P（s*＝s｜Θ）最大化，即：

其中s∈Ω是可能风险源节点的集合。在这里，只有节点的子集Ω⊆V Q是可能的候选源：V Q节点集之间至少有一条共享路径连接网络中被污染的节点o k∈Ω。除非事先有关于源节点位置的信息，假设s*的先验分布是均匀分布，即使得为最大似然估计。

解决该问题的主要挑战是求P（Θ｜s*＝s）的最大似然估计。

在位置的疾病报告的概率取决于通过网络从风险源s到所有观察结果ok∈Θ的路径。

但是，从s到每个疾病报告节点o k∈Θ可能的路径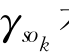有多条，风险源的概率是s等于每个路径排列的总概率。引入如下定义，来计算所有排列的风险源可能性：

为网络G从s到o的所有可能路

πs，从某风险源s到疾病报告位置的k条路径ok∈Θ的某一特定排列。形式上，πs是元素在路径组上的笛卡尔积，即所有s-cascades的集合，或从s到每个o k∈Θ的路径的所有排列，即：

根据这些定义，风险源可能性可以写为所有排列的总概率

其中P（Θ｜s，πs）＝1，根据定义，疾病报告位置ok∈Θ是路径的终节点。(www.xing528.com)

求解该方程就是找到对于所有πs∈ΠS的总概率。对于逐个Pπs｜（）s可以在每个相邻节点对（i，j）根据和转移概率p ij展开为：

第二个等式为到每个疾病报告的独立路径第三个等式为跟路径相关的总概率。

则似然概率可以描述为如下形式：

计算上式中的似然概率需要穷举对于ΠS中的每一个πs的所有路径对于大食品供应网络而言，即使疾病报告很少，也会出现组合爆炸。

Abigail提出上述公式可以转化为：

似然概率的计算只需要对矩阵A作一次简单运算，其中：

上式可以计算等式（4.6）的最大似然，用于从所有可能风险源s∈Ω中定位源节点s，使得后验概率最大。

对每一个可能的风险源s∈Ω，计算后验概率：

对于某标准化常数c，构建源节点s∈Ω的概率分布，以定位最可能的风险源头。