复杂网络模型的演化过程

正如前所述，关于复杂网络的研究是逐步发展的，从网络拓扑结构的角度来看，主要包括规则网络（Regular Network）、随机网络（Random Network）、小世界网络（Small-World Network）和无标度网络（Scale Free Network）。

（1）规则网络（Regular Network）

常见规则网络如图3.1所示，包括：全局耦合网络（globally coupled network）（图a）、最近邻耦合网络（nearest-neighbor coupled network）（图b），以及星形网络（star network）（图c）。

全局耦合网络又称完全网络，该网络任意节点之间都存在直接连边，其平均最短路径为1，最大集聚系数也是1。然而大多数实际网络都比较稀疏，边数一般为O（N），而不是O（N 2）。

最近邻耦合网络是稀疏规则网络，其中每个节点都只和它最近的左右各k/2个邻居节点相连，图中（k＝4），围成一个环形网，每个节点具有相同的度数和集聚系数。度数服从δ函数分布，即：

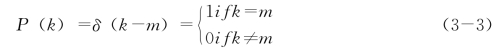
平均度：k＝m，与N无关。平均集聚系数为C＝3（k-2）/4（k-1），集聚程度较高。如对于图（b），有C＝1/2，与N无关。当k→∞，C→3/4。当k值较大时，最近邻耦合网络的集聚系数约为3/4，集聚度较高。然而，对于给定k，当N趋于无穷大时，其平均最短路径长度也趋于无穷大。

星形耦合网络也很常见，它有一个中心节点，其他节点与且只与该中心节点相连。该网络平均最短路径长度L→2（N→∞），集聚系数C→0。该网络是不稳定的，如果中心节点遭遇故障，所有网络节点之间将失去连接。

（2）随机网络（Random Network）

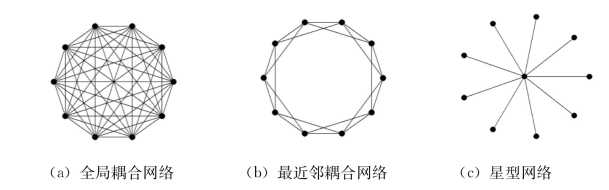
图3.1　三种规则网络拓扑结构(www.xing528.com)

由匈牙利数学家Erdös和Rényi建立的随机图理论（Random graph theory）在数学上开创了复杂网络结构系统性分析之先河。ER网络可描述为：在由N个顶点、（N-1）/2条边构成的图中，随机选择g条边进行连接，形成一个随机网络，记为GN，g，因此N个节点、g条边能够组成个不同的网络，每个网络出现的概率相同，其网络结构如下图（a）所示。ER网络的节点度数服从泊松分布，平均度和节点数N成正比，平均集聚系数与节点总数N成反比，平均距离与ln N成正比［74］。ER网络从提出到90年代末的近四十年里，很多大规模网络都用ER随机图来描述，即假设网络形成过程中，节点间的连接完全随机。随着小世界网络和无标度网络的提出以及计算机处理能力的提升，科学家们同时也发现实际网络的许多统计特征并不能完全用ER随机网络模型来刻画。

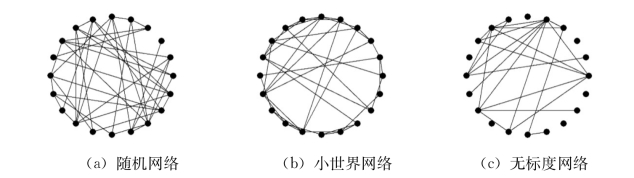
图3.2　几种复杂网络拓扑结构

（3）小世界网络（Small World Network）

复杂网络是一种位于规则网络与随机网络之间的网络结构，为刻画这两者之间的联系，Watts和Strogatz在Nature上发表了一篇著名的论文：小世界网络的集体动力学［75］，对复杂网络研究产生了重要影响。图2.6（b）是我们用Pajek生成的一个小世界网络。小世界网络的生成过程是从规则网络开始，以概率p随机地选择每条边进行重新连接，即边的一个端点保持不变，再随机地从其他网络节点中任选一个建立连接，如果碰上自连接和重复边，则重新选择。这样，当p＝0时，没有“随机跳跃边”，表现为规则网络；当p＝1时，所有边都随机重连，模型转化为ER随机网络；而在0＜p＜1时，建立了一个位于规则与随机之间的网络模型。“小世界网络”的长程连接大大地缩小了网络的平均路径长度。小世界模型的平均集群系数的期望值为：C＝3（k-2）（1-p）3/4（k-1），与N无关。在0＜p＜1范围内p可以取很多值，使得小世界模型表现出很多不一样的特性，既有规则网络平均集聚系数较大的特点，又有随机网络平均距离较小的特点。小世界模型有其深刻的社会根源，因为在社会系统中，多数节点只与最近节点交互，但也存在不少节点跟远程节点建立连接，通过这些节点，网络节点距离更短了，世界变小了，这正是称为小世界网络的原因。

（4）无标度网络（Scare Free Network）

ER随机网络和WS小世界网络从某种意义来说都是匀质网络，其度数服从泊松分布，即度数概率在平均值k处取最大值，当小于或大于k时，概率快速变小。直到Barabási、Albert于1999年在Science上发表随机网络标度的涌现［76］论文，首次提出了无标度网络模型，复杂网络理论发展又迈出了新的一步。BA模型指出许多实际的复杂网络都具有“无标度性”。许多实际的大规模无标度网络，精确或近似地遵循幂函数的度分布，P（k）∝k-γ（幂指数通常为2≤γ≤3）。无标度网络中绝大多数节点的度数相对很低，也存在少量度值相对很高的节点。因此无标度网络具有较强的“异质性”，即不均匀、非平衡以及复杂基础上的有序。无标度网络的一个重要特点就是“择优连接”，即形成网络过程中，连接某个节点的概率单调依赖于该节点的现有度数。如果节点度数越高，则越有可能被选择连接；反之，则被选择的概率越小，表现出一定的马太效应，如图（c）所示，节点度数分布很不均匀，有些节点有很多条边，有些节点的连边很少甚至没有。

Albert等人推导出了无标度网络的平均距离函数：l≈ln（N）/lnln（N）（其中N为网络节点总数）［83］。汪小帆等人综合上述各类型复杂网络的分析并与现实网络的特性进行比较［79］，得到下表：

表3.1　各类型复杂网络与现实网络的特性对比