法向侧隙计算方法与偏移联轴器设计

（1）内、外齿面间的最小法向侧隙 当轴线有角位移Δα时，鼓形齿与内齿产生相对位移，鼓形齿上各点将相对其在Δα=0°时的位置产生位移，此位移量在内齿法线上的投影称为鼓形齿的法向位移量。将各对齿沿分度圆圆周展开，即可得齿的相对位置图，如图15-6所示。

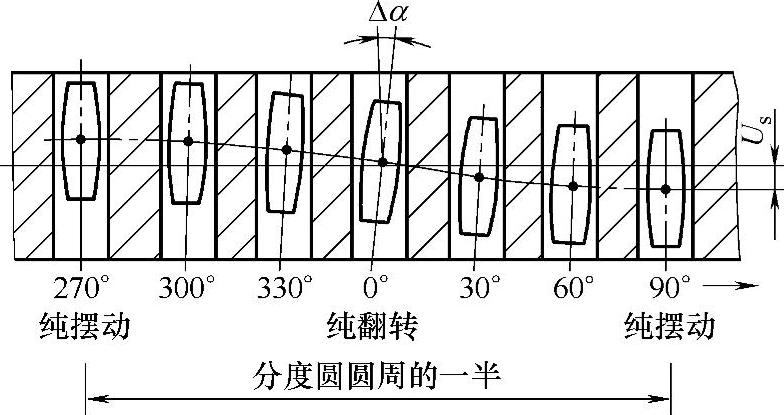
图15-6 齿的相对位置

由图15-6和图15-7可知，在ϕ=0°及180°时，鼓形齿为翻转运动，齿上各点绕齿中心回转；在ϕ=90°及270°时，鼓形齿为摆动运动，齿上各点沿齿宽方向偏摆；在其余位置则为这两种运动的合成。联轴器每转一周，任意一对齿都要按图15-6的规律依次通过每个位置，而任一鼓形齿上各点的法向位移量也随位置角ϕ变化。任一对内外齿的左、右齿面间的最小法向侧隙J_Lmin、J_Rmin应同时能满足鼓形齿左、右齿面的最大法向位移量，可近似按下式计算

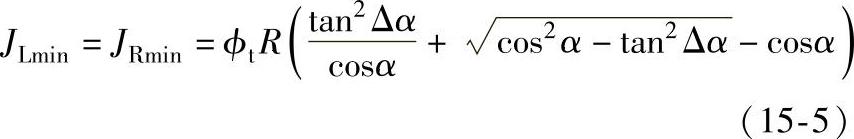
式中 ϕ_t——曲率系数；

R——鼓形齿位移圆半径；

α——压力角；

Δα——角位移。

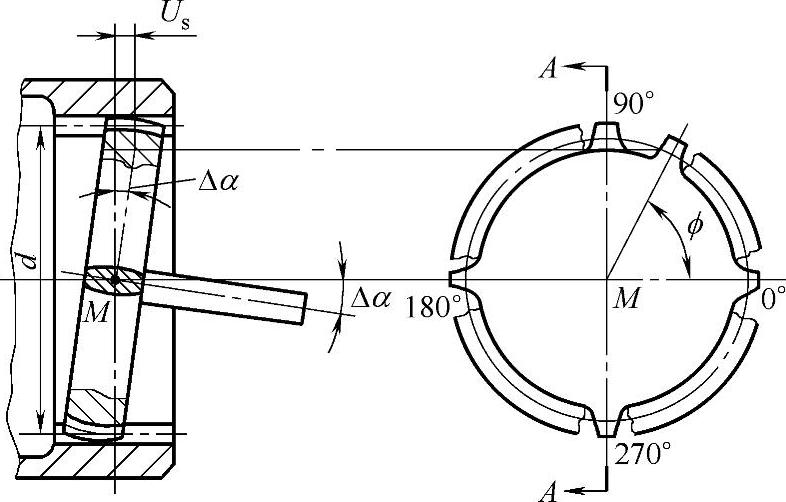
图15-7 鼓形齿的偏移

（2）联轴器的最小理论法向侧隙 联轴器的最小理论法向侧隙J_nmin为J_Lmin和J_Rmin之和。

J_nmin=JLmin^+JRmin

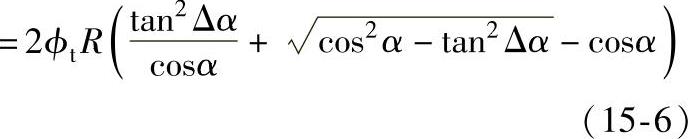
联轴器的最小理论圆周侧隙J_tmin为

联轴器内、外齿不产生齿宽边缘接触的条件为

(www.xing528.com)

式中 b₁、b₂——外、内齿齿宽。

直齿联轴器的最小理论法向侧隙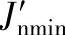为

（3）联轴器的最小设计法向侧隙 联轴器的最小设计法向侧隙除保证J_nmin外，还必须考虑对制造误差的补偿量δ_n1、外齿轴套与轴过盈连接时轴套胀

大的补偿量δ_n2。补偿量的计算分别如下：

δ_n1=[（F_p1+F_p2）cosα+（f_f1+f_f2）+（F_g+F_β2）]（15-10）

式中 F_p2、F_p1——内、外齿齿距累积公差；

f_f2、f_f1——内、外齿齿形公差；

F_β2——内齿齿向公差；

F_g——鼓形外齿齿面鼓度对称度公差，见表15-4。

δ_n2=Δdsinα（15-11）

式中Δd——外齿轴套直径胀大量，按过盈连接

计算。

联轴器的最小设计法向侧隙J_n，为

J_n=J_nmin^+δn1^+δn2（15^-12）

对一般的小过盈加键连接，δ_n2可忽略不计。