由图12-12可知,Qi、Pi与Ni三个载荷之间存在如下关系:

Pi=Nitanαi(12-36)
式中,αi为滚子与内齿圈的接触角(见图12-9)。它与理论齿廓曲线的压力角相等,可由下式计算:
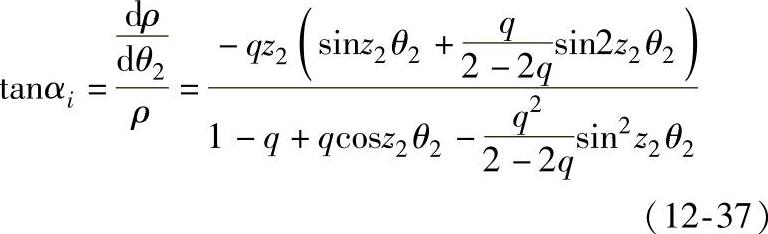
式中,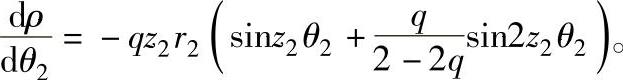
由理论齿廓曲线的极坐标方程式(12-9)可知,当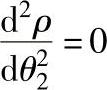 时,理论齿廓曲线出现拐点,可由
时,理论齿廓曲线出现拐点,可由
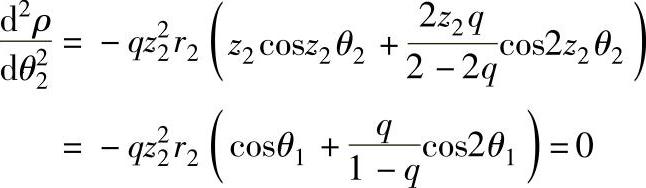
求得θ1=z2θ2(约为89°,确切的值与所取的偏心系数q值有关),此时压力角αi有极大值,为38°左右。
为了求取Qi、Pi与Ni三个载荷,假定偏心轮、内齿圈与滚子架的刚度很大,即假定为刚体,而滚子有接触变形。当偏心轮顺时针方向转动时,y轴左边滚子与内齿圈有离开的趋势,而y轴右边的滚子与内齿圈发生接触,且偏心轮对各滚子有一个正压力。设各个滚子沿与偏心轮接触点的法向变形呈正弦分布,即
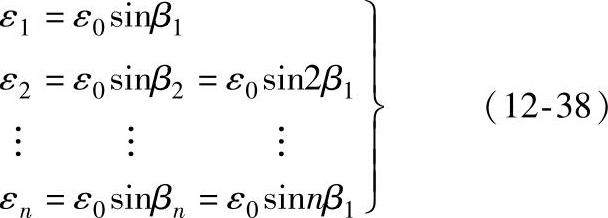
式中 ε0——对应于最大正压力Nmax时的最大变形;
β1——相邻两滚子的中心夹角,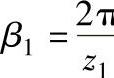 ;
;
εi——各滚子沿与偏心轮接触点的法向变形,
i=1,2,…,n。
滚子变形与正压力的关系如下:
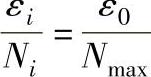 (https://www.xing528.com)
(https://www.xing528.com)
即
Ni=Nmaxsinβi(12-39)
由于滚子活齿行星传动通常也采用两排滚子,考虑到载荷分配不均匀,每排滚子传递的转矩增大10%,即
T1=0.55TV(12-40)
而
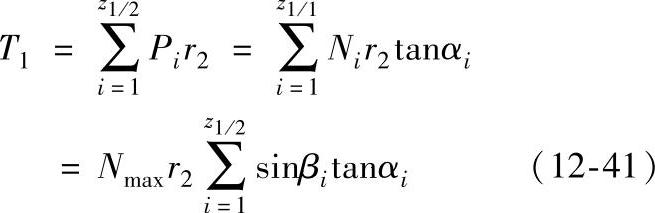
式中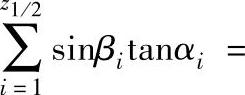
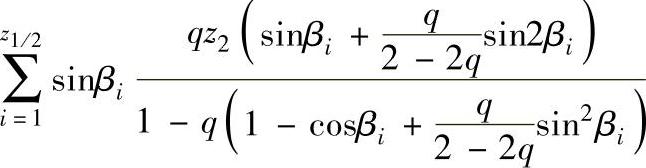
因为q较小,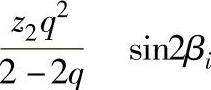 和
和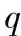
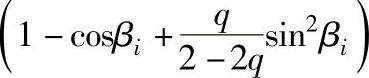 可略去不计,并根据现有资料,qz2的平均值约为0.9,所以
可略去不计,并根据现有资料,qz2的平均值约为0.9,所以
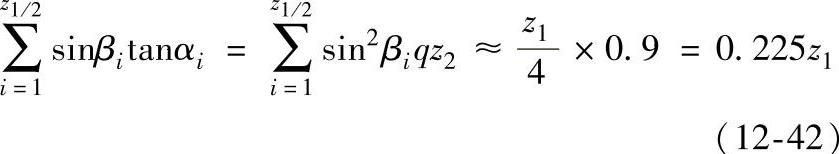
将式(12-42)代入式(12-41),并考虑到制造与安装的误差引起受力不均匀,需将载荷适当放大,乘上一个载荷放大系数φ=1.35,经整理得到
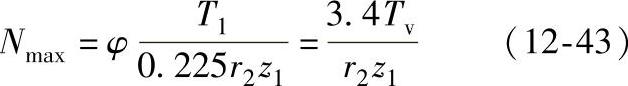
根据式(12-39)、式(12-36)与式(12-35)可分别得到
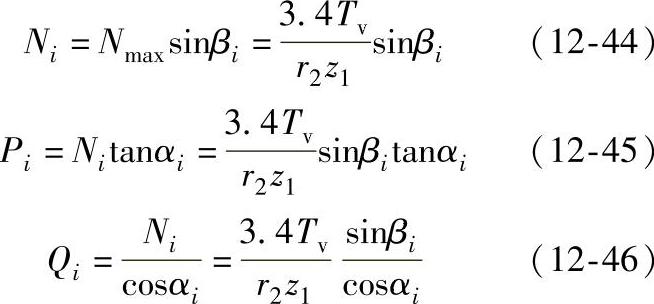
从式(12-45)与式(12-46)中可知,当βi=89°左右时,αi有最大值,为38°左右,则Pi与Qi也有最大值。
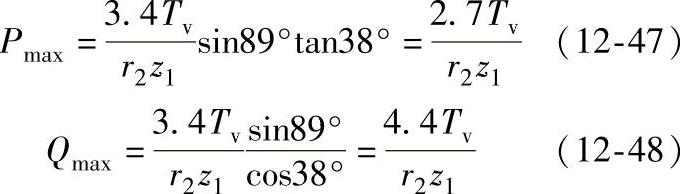
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




