为了避免较为复杂的齿廓曲线的加工,在不影响啮合精度的条件下,可采用其他近似的容易加工的齿廓曲线来替代。密切圆是一种较好的近似齿廓。它与活齿的包络曲线的误差微小,并且采用半圆齿廓,去掉凸啮合部分线段,降低了总的诱导曲率,有利于提高承载能力。
(1)滚子活齿包络曲线 在求包络曲线时,假定输出滚子架固定,当输入轴转过θ角时,内齿圈仅转过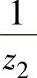 θ角。由图12-10可知:
θ角。由图12-10可知:
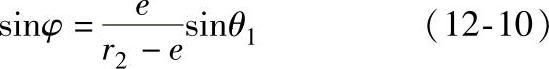
ρ=ecosθ1+(r2-e)cosφ(12-11)
活齿在Ozx1y1坐标系中的圆方程
x21+y21=r2z
进行坐标平移,得
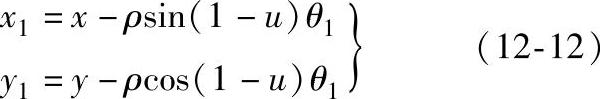
式中 ρ——活齿中心Oz离O2的距离;
u——活齿数与内齿圈齿数之比,即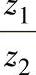 。
。
将上式代入圆方程得
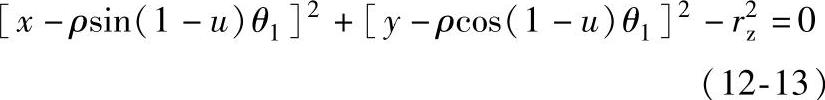
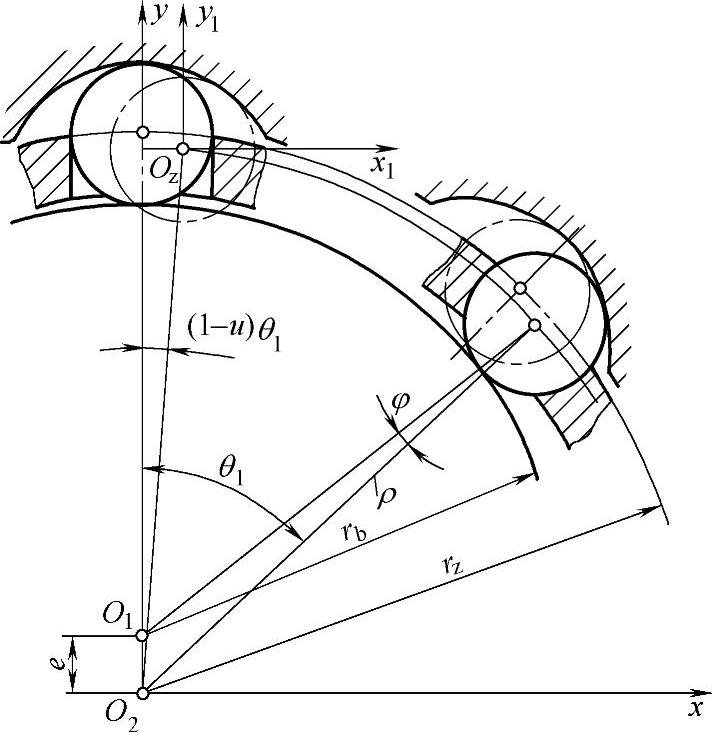
图12-10 滚子活齿包络曲线
现求滚子活齿的包络,将式(12-13)对θ1角偏导,并经整理得
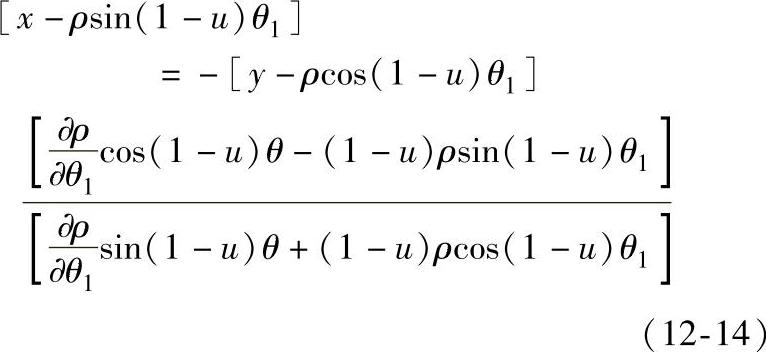
设
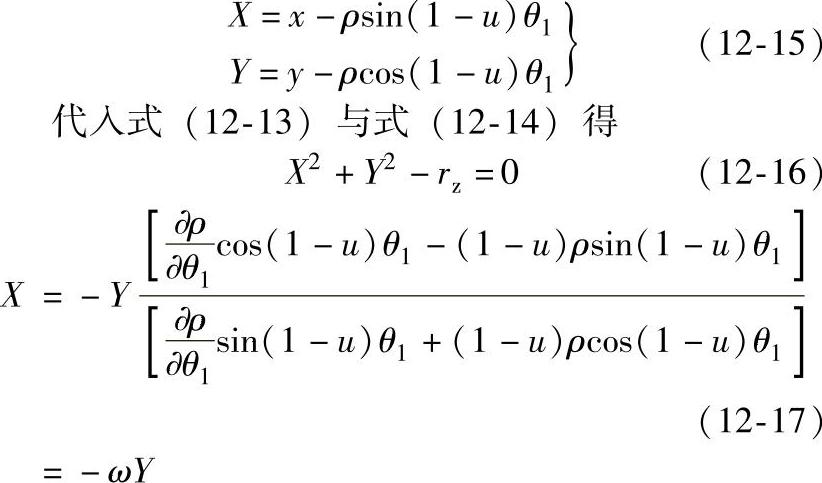
式中
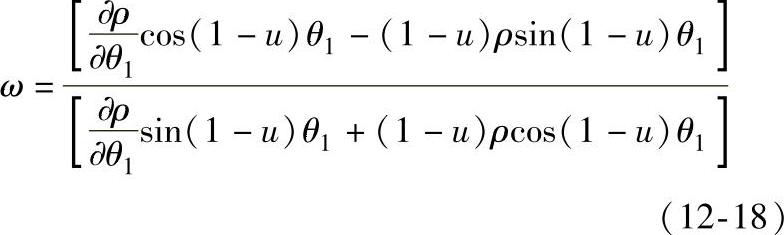
现将式(12-18)中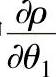 化简。由式(12-11)对θ1偏导得
化简。由式(12-11)对θ1偏导得
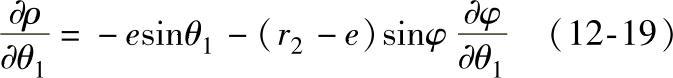
由式(12-10)对θ1偏导,经整理得
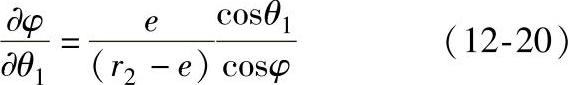
又因为
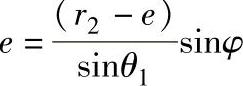
将上两式一起代入式(12-19)得
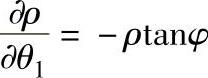 (https://www.xing528.com)
(https://www.xing528.com)
再将上式代入式(12-18)得
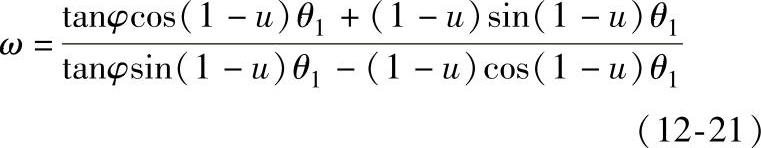
将式(12-17)代入式(12-16)得
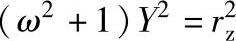
从而解得
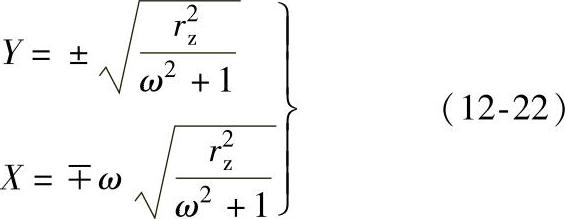
将以上X、Y代回式(12-15)得
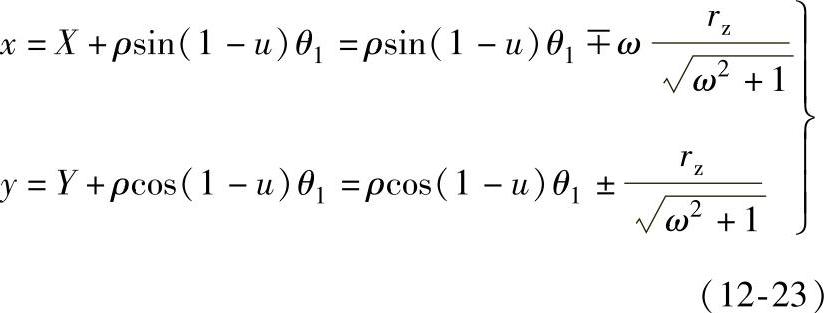
这就是总体坐标系中的包络线方程。由于滚子活齿行星传动装置需要外包络曲线,所以取滚子活齿包络曲线方程为
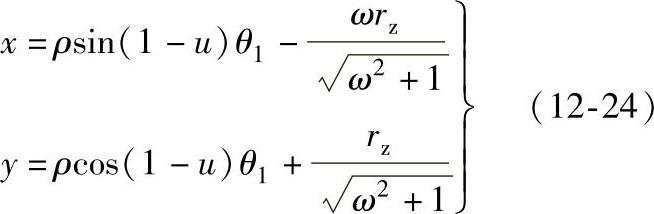
(2)包络曲线的密切圆 由于滚子活齿包络曲线在制造上也具有一定的困难,可采用密切圆来替代包络曲线。
1)密切圆圆心。设过包络线及滚子中心的连线方程为
y=Kx+b(12-25)
由于在Ozx1y1坐标系中,滚子中心点坐标为x1=0,y1=0,因此可利用式(12-12)得到滚子中心点在O2xy坐标系中的坐标式
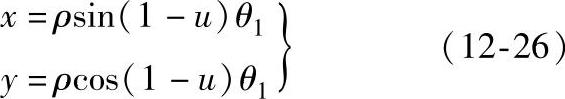
将上式代入式(12-25)得
b=ρcos(1-u)θ1-Kρsin(1-u)θ1(12-27)
由式(12-27)、式(12-24)和式(12-25),可解得

由式(12-28)、式(12-27)及式(12-25),可得
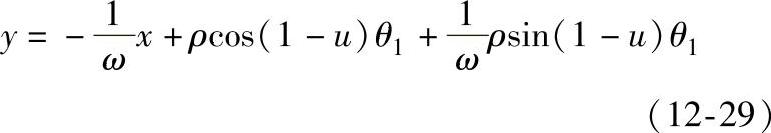
为了避免加工干涉,须使齿廓中心在y坐标轴上,因此密切圆的中心点坐标为
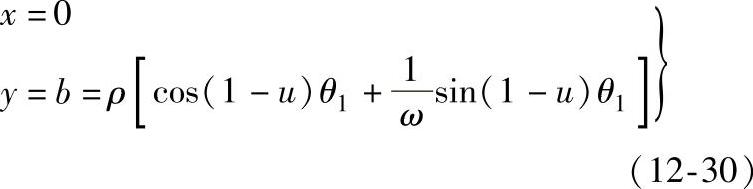
2)密切圆方程。通过作图分析,当传动参数选择恰当,滚子活齿圆的轨迹有密集的汇交中心,密切圆半径趋近于滚子直径。调整参数rz与e可使汇交点中心落在y坐标轴上,因此密切圆关系式可写成
(y-b)2+x2=(2rz)2
将式(12-24)与式(12-30)代入上式,可得滚子半径
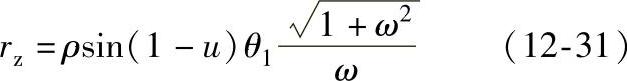
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




