【摘要】:理论齿廓曲线的直角坐标方程 现用相对速度法推导齿廓曲线方程。如果用与内齿圈相连的坐标系O2x2y2来描述理论齿廓,其转轴方程为将式代入上式,经整理得理论齿廓方程:式中实际齿廓为理论齿廓的等距曲线。滚子中心Oz到偏心轮中心O1的距离为理论齿廓上任一点Oz到内齿圈中心O2的距离为式中 q——偏心系数,。由图12-9可知,OzO1sinφ=esinθ1,即图12-9 理论齿廓曲线极坐标当q很小时,φ角较小,则将式代入式,经整理得到理论齿廓曲线的极坐标方程为
(1)理论齿廓曲线的直角坐标方程 现用相对速度法推导齿廓曲线方程。所谓相对速度法,就是将行星轮系各构件加上一个与转臂反向的公共角速度ωH,使行星轮系转换成为定轴轮系。这样内齿圈中心O2与偏心套中心O1都变为不动,如图12-8所示。当活齿推动了输出滚子架转过θ角时,则内齿圈所转的角度为μθ,即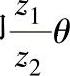 。
。
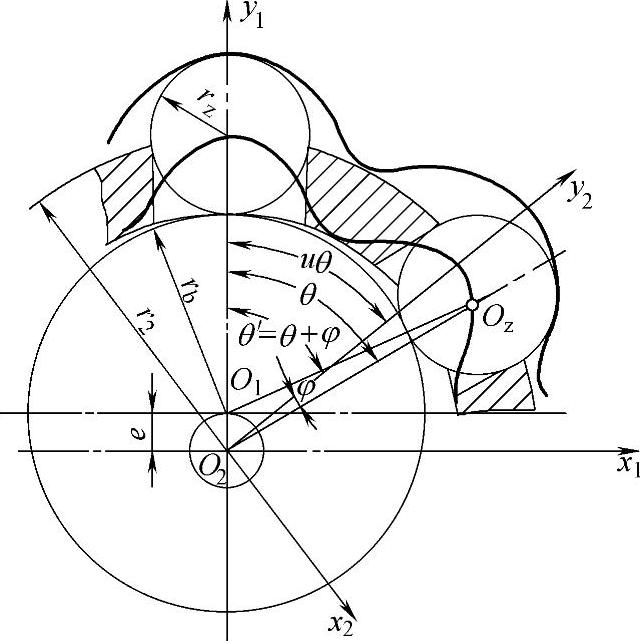
图12-8 理论齿廓曲线直角坐标
在O2x1y1坐标系中,活齿中心点(x1,y1)的轨迹方程为
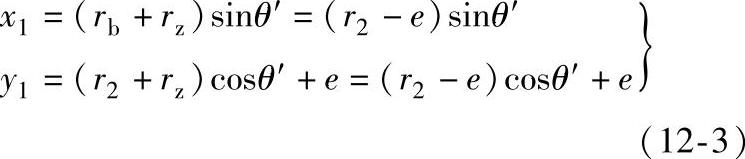
式中 rb——转臂轴承外圈半径;
rz——滚子活齿半径;
r2——内齿圈分度圆半径;
θ′=θ+φ;
e——偏心距,也即中心距。
如果用与内齿圈相连的坐标系O2x2y2来描述理论齿廓,其转轴方程为
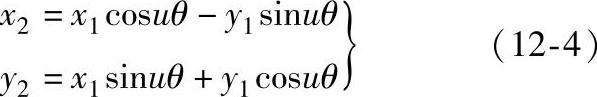
将式(12-3)代入上式,经整理得理论齿廓方程:
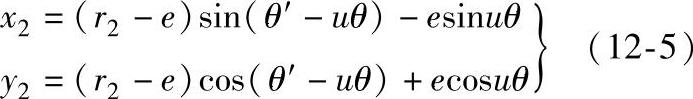
式中
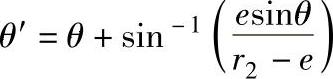
实际齿廓为理论齿廓的等距曲线。内齿圈的齿根圆半径(https://www.xing528.com)
rf2=rb+e+2rz=r2+rz
内齿圈的齿顶圆半径
ra2=rb-e+2rz=r2-2e+rz
(2)理论齿廓曲线的极坐标方程 如果将滚子架固定,当偏心轴顺时针方向转动θ1角时,则内齿圈也顺时针方向转过θ2角,且θ1=z2θ2,如图12-9所示。滚子中心Oz到偏心轮中心O1的距离为
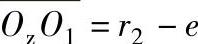
理论齿廓上任一点Oz到内齿圈中心O2的距离为
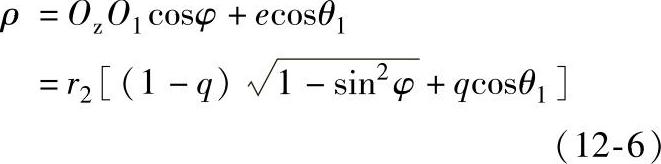
式中 q——偏心系数,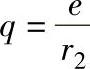 。
。
由图12-9可知,OzO1sinφ=esinθ1,即
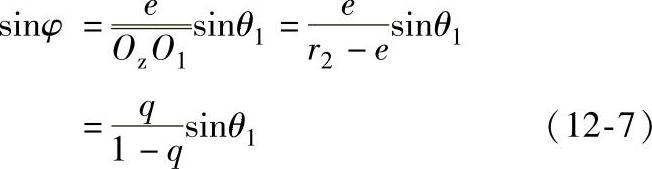
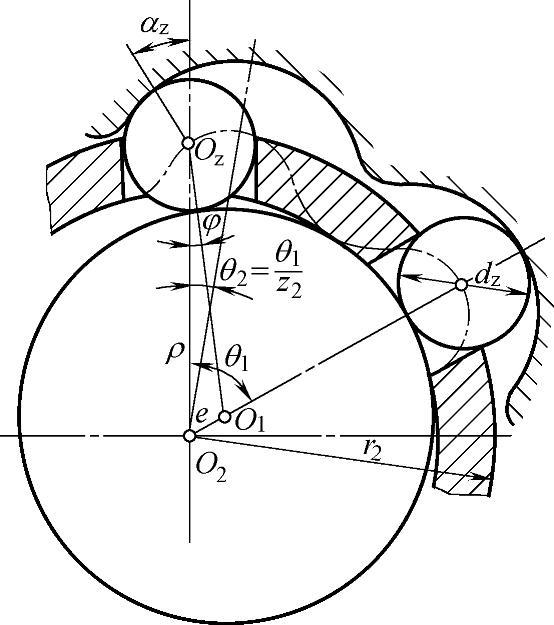
图12-9 理论齿廓曲线极坐标
当q很小时,φ角较小,则
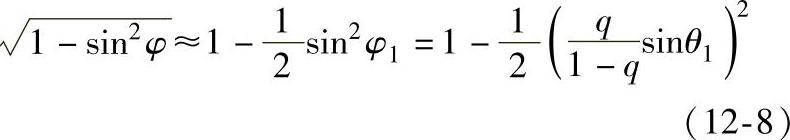
将式(12-8)代入式(12-6),经整理得到理论齿廓曲线的极坐标方程为
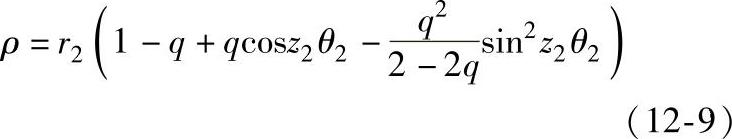
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




