1.要求设计K-H-V(N)型少齿差传动,内齿圈固定。
已知:模数m=1.5mm,压力角α=20°,传动比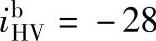 。
。
解 1)几何参数计算。
齿数差 zε=zb-zg=2
齿顶高系数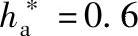
初选啮合角 α′=35.5°
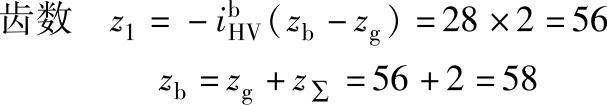
中心距
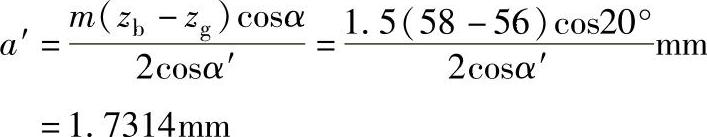
取a′=1.73mm。
啮合角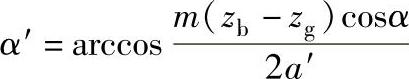
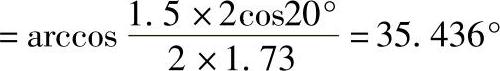
确定重合度的预期值[εα]=1.10
变位系数的初始值,取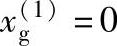
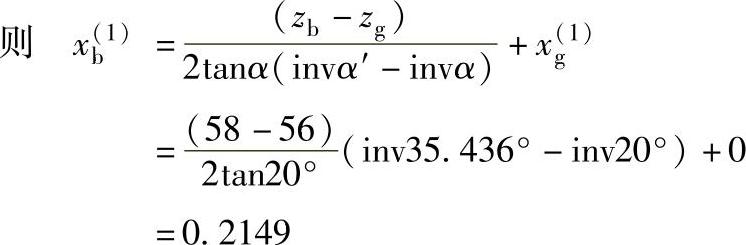
分度圆直径dg=mzg=1.5×56mm=84mm
db=mzb=1.5×58mm=87mm
齿顶圆直径
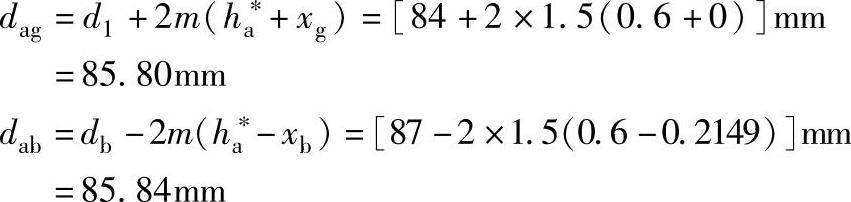
齿顶圆压力角
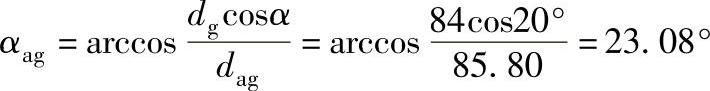
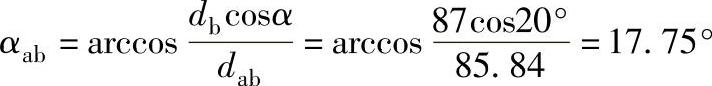
验算重合度
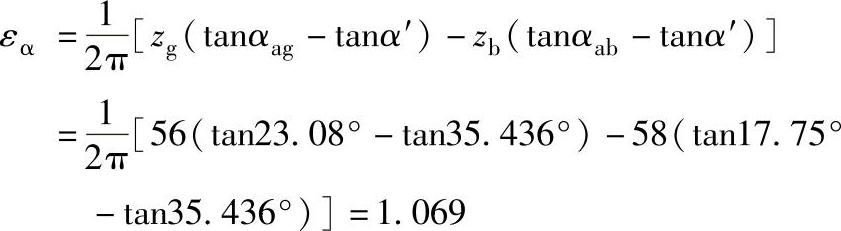
重合度小于预期值的要求,必须按[εα]的要求用迭代法重新确定变位系数。
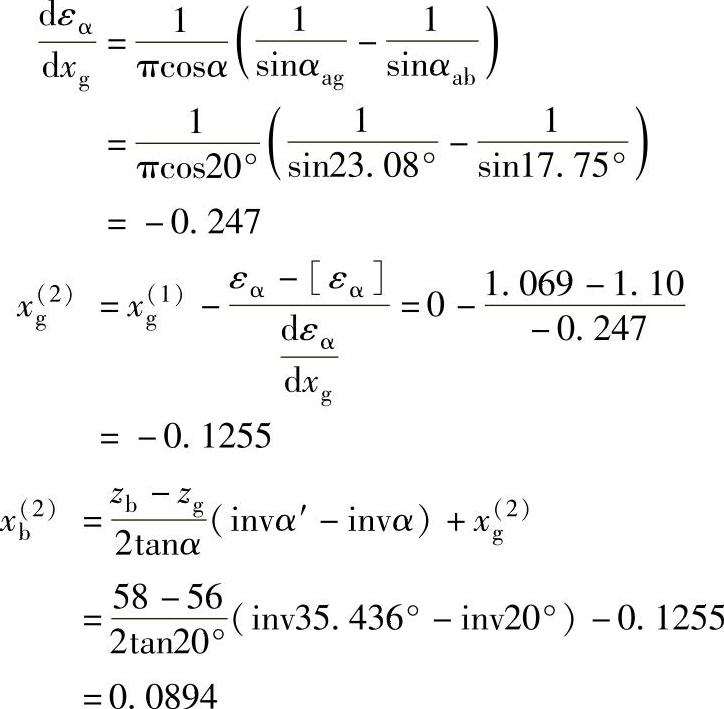
重新确定几何参数
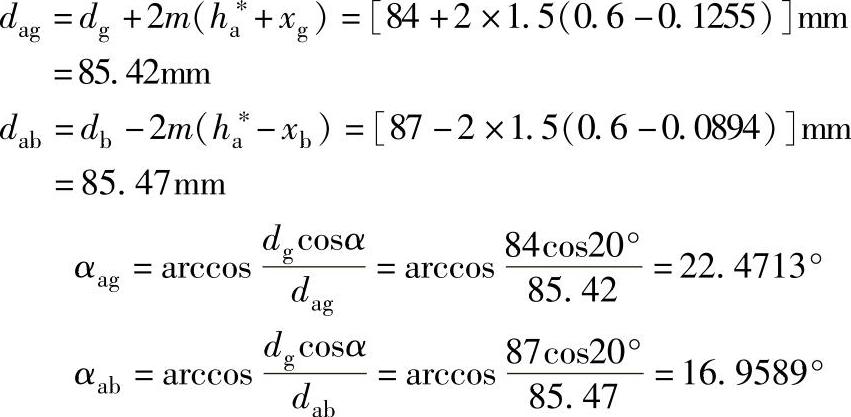
重新验算重合度
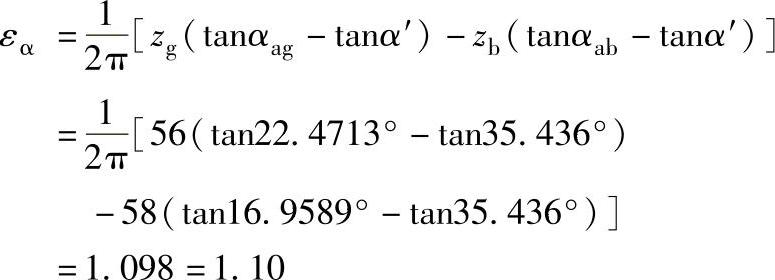
已满足预期值的要求。
验算齿廓重叠干涉
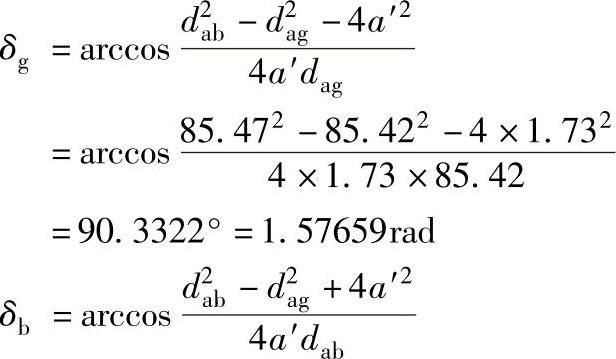

Gs=zg(invαag+δg)-zb(invαab+δb)+z∑invα′=56(inv22.4713°+1.57659)-58(inv16.9589°+1.55361)+2inv35.436°=0.062>0.05
已满足规定值的要求。
2)插齿刀参数计算。
插齿刀齿数 z0=34
公称分度圆直径 d0=50mm
实际分度圆直径 d0=mz0=1.5×34mm=51mm
顶圆直径

齿顶高系数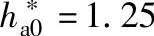
变位系数

由上述参数按GB/T 6081—2001选用碗形直齿插齿刀。
3)内齿圈齿根圆直径计算。
插齿刀与内齿圈的啮合角α0′b
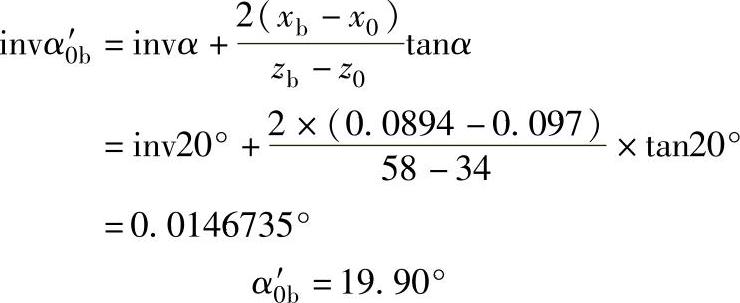
插齿中心距

内齿圈根圆直径
dfz=2a0′b+da0=(2×17.987+55.04)mm=91.02mm
4)齿轮强度计算。渐开线少齿差行星传动为内啮合传动,又采用正角度变位,其齿面接触强度与齿根弯曲强度均提高,且齿面接触强度远大于齿根弯曲强度,同时又是多齿对啮合,所以内、外齿轮的接触强度一般可不进行验算。齿根弯曲强度的计算方法与普通齿轮大致相同,这里不再论述。
2.零齿差齿轮副的加工
(1)外齿轮的加工
1)试切法。当齿轮用滚齿或插齿加工到径向变位时的公法线长度后,再施行切向变位加工,通常可将分度交换齿轮脱开,用扳手扳动分度蜗杆上的交换齿轮拨过一齿,进行试切,看一看分度交换齿轮拨过一齿后进行切齿加工,其公法线的变动量为多大,从而可计算出加工切向变位终了的公法线长度所需拨过的齿数。也可用压靠百分表,将齿轮滚刀进行轴向往返移动,进行试切,直至加工到切向变位终了的公法线长度便可。当切向变位系数很小时,在齿顶不变尖的前提下,也可直接采用径向变位的加工法加工到所需的公法线长度。但上述方法较费时,要反复试,下面介绍计算法。
2)计算法。计算法即用计算方法确定分度交换齿轮所拨过的齿数A。
图9-54所示为外齿轮公法线大小的变动情况,虚线位置表示齿廓径向变位终了的齿形。
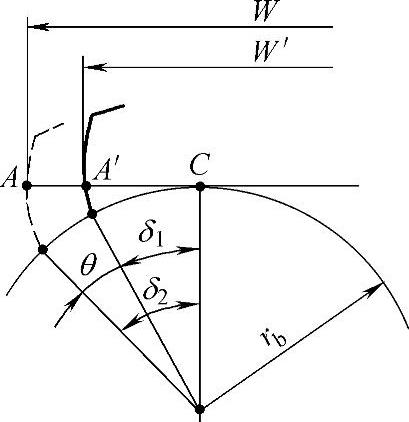
图9-54 外齿轮公法线变动
由图9-54可知

式中 W′——零件图上给定的切向变位终了时的公法线长度;
W——径向变位终了时所测的公法线长度;
db——基圆直径。
要达到图样上所规定的公法线长度,必须让齿坯相对于刀具向左、右分别转动角度θ。现以Y54A型插齿机为例,说明其角度的计算。
在图9-55中,设交换齿轮的齿数z1、z2、z3和z4,则
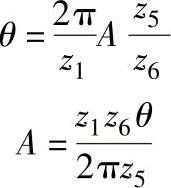
式中 z1——与机床工作台分度蜗杆相连的交换齿轮的齿数;
z5——机床分度蜗杆的头数;
z6——机床分度蜗轮的齿数;
A——保证齿坯相对于刀具转动θ角时,所拨动交换齿轮的齿数。
上式也用于滚齿加工时的计算。

图9-55 Y54A型插齿机有关传动部分
(2)内齿圈的加工 同样也可采用试切法,但较费时。今将交换齿轮扳动齿数A的计算作一叙述。
图9-56所示的虚线表示齿廓径向变位终了时的齿形。实线表示齿廓切向变位终了时的齿形。由图可知(https://www.xing528.com)
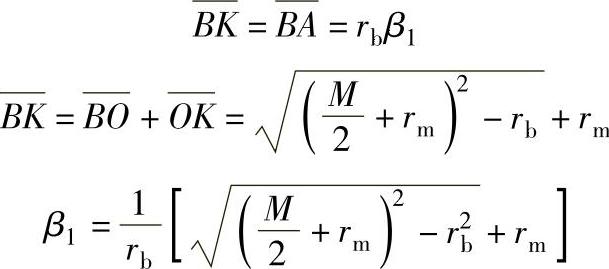
式中 rb——基圆半径;
M——径向变位终了时的量柱距;
rm——量柱(或钢球)半径。

式中 z——内齿圈齿数;
α——齿形角(分度圆压力角),α=20°;
x——径向变位系数。
δ1=β1-αm
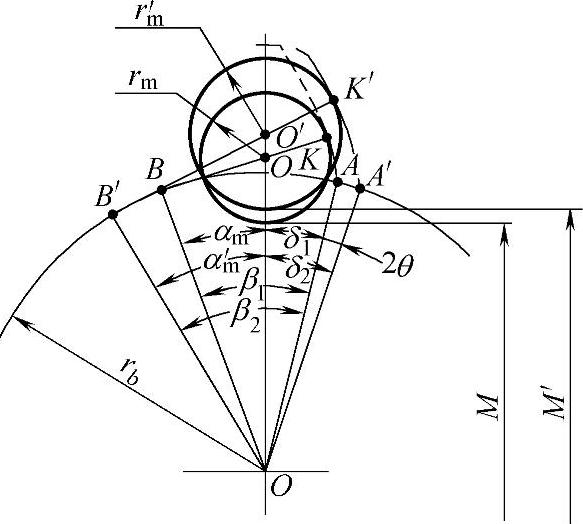
图9-56 内齿圈的变位与测量
上式为加工内齿圈径向变位时,齿坯转角δ1的计算式。同理,也可得出内齿圈在径向变位后,再进行切向变位时的计算式
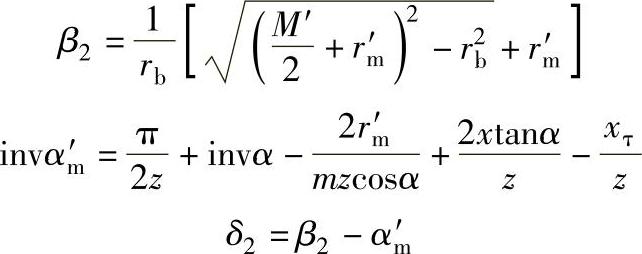
式中 M′——切向变位后的量柱距;
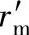 ——量柱(或钢球)半径;
——量柱(或钢球)半径;
xτ——切向变位系数(轮齿变薄时为负值)。
由于是分别向正反向扳动交换齿轮,则齿数相同,所以
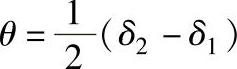
与前相同,使齿坯相对于刀具转动θ角时,所拨动交换齿轮的齿数A的求法见9.8节2(1)。
由上述方法计算后,进行切向变位加工十分方便,无需反复试切,不易出差错,有利于推广零齿差输出机构的应用。
3.对于双内啮合2K-H(NN)型的少齿差行星齿轮传动,其行星轮是个齿数不同的双联齿轮,存在着不便于用滚齿机加工齿轮等缺点。建议当减速器的传动比i=20~100时,可用一个齿轮代替双联行星轮,即公共行星轮,这样可使结构简单,加工方便。
具有公共行星轮内啮合2K-H(NN)型行星齿轮传动,其三个基本构件是两个中心轮2K和行星架(即偏心轴)H。为了获得较大的传动比,两个中心轮的齿数差为1,如图9-57所示。齿数较多的中心轮与公共行星轮采用标准齿轮,齿数较少的中心轮采用变位齿轮,使其满足同心条件。若公共行星轮用z1表示,固定中心轮的齿数用z2表示,输出中心轮的齿数用z3表示,其结构图如图9-58所示。其传动比为

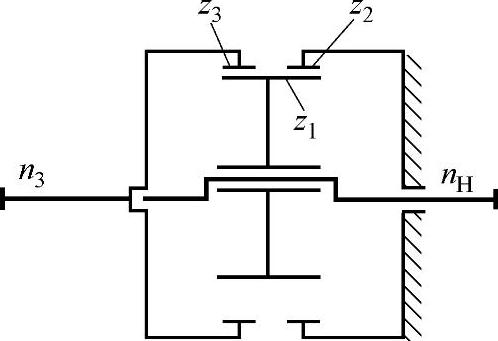
图9-57 2K-H(NN)型传动简图(公用行星轮,传动比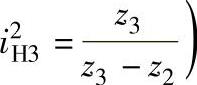
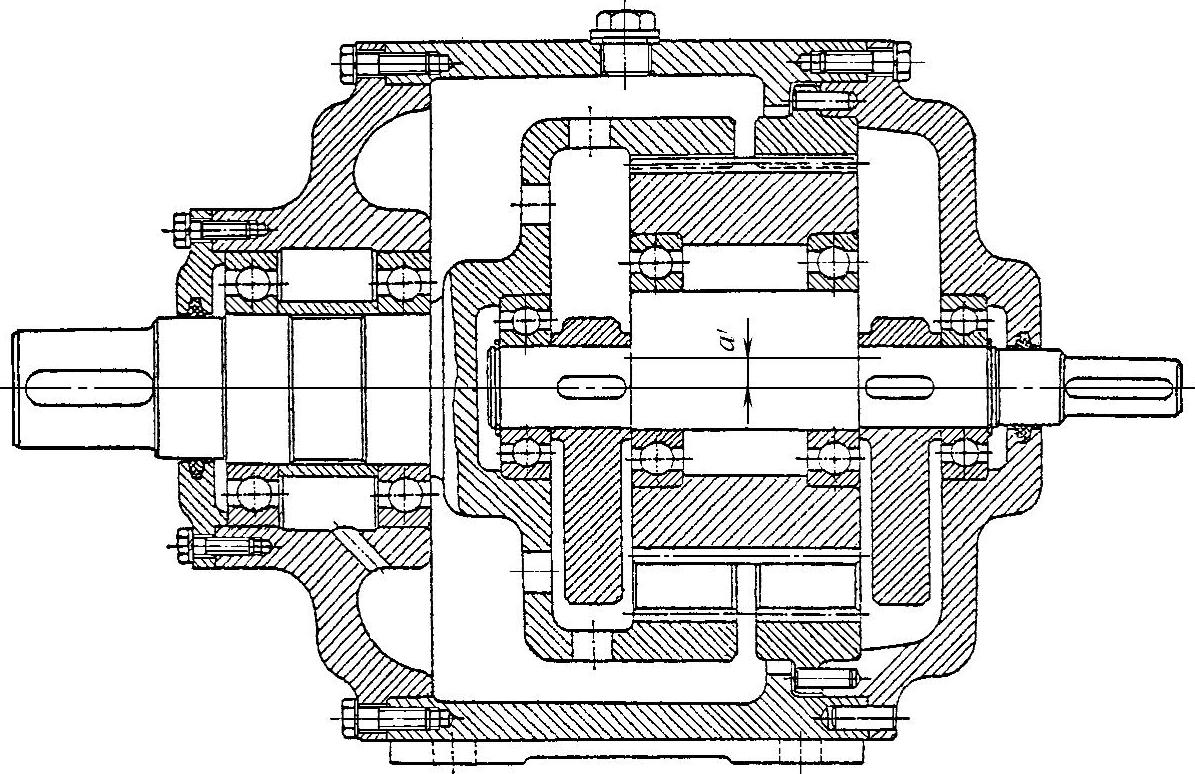
图9-58 2K-H(NN)型少齿差行星齿轮传动(公共行星轮)
为了得到较大的传动比,一般选用
z3-z2=1
于是,传动比的计算公式可写成
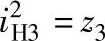
即传动比等于输出内齿圈的齿数。
例如,某一单梁起重机大车运行机构的速度,确定减速器的传动比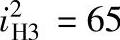 ,则输出内齿圈齿数z3=65。若z3-z2=1,则z2=z3-1=64。
,则输出内齿圈齿数z3=65。若z3-z2=1,则z2=z3-1=64。
公共行星轮的齿数z1,由z1-z3标准内啮合齿轮副不发生齿廓重叠干涉的条件确定,根据有关文献推荐,取
z3-z1>8
本设计取z1=z3-8=57,z1-z3标准齿轮内啮合副的中心距为
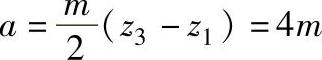
由于z1-z3内啮合副的内、外齿轮均是标准齿轮,则啮合角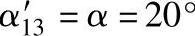 。
。
根据同心条件,确定z1-z2的啮合角 ,即
,即
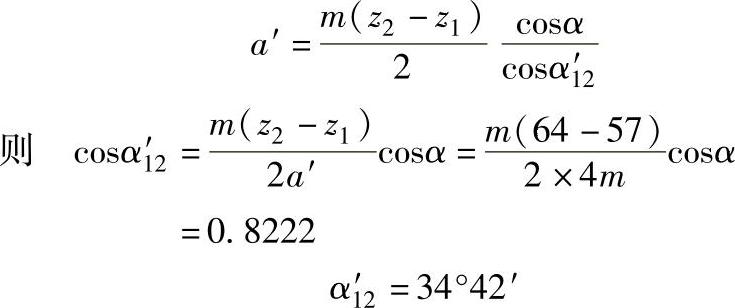
变位系数x2,由无侧隙啮合方程式可得
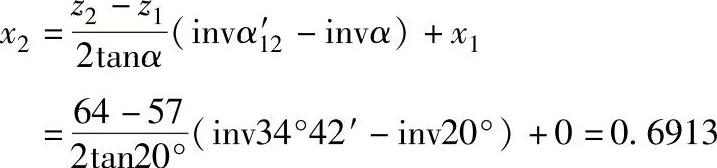
其中,x1=0,因公共行星轮是标准齿轮。
中心距变动系数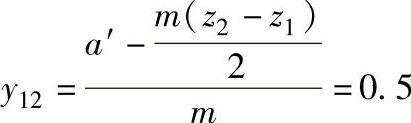
然后验算z1-z2内啮合齿轮副的齿廓重叠干涉和重合度,要求:
1)不发生齿廓重叠干涉,希望Gs≥0。
2)重合度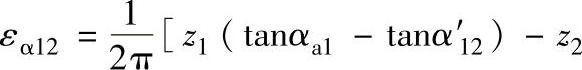
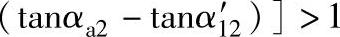 。
。
若不满足要求,应通过调整变位系数x2,或改变z2、z3的齿顶高系数 ,直至满足两内啮合副的要求为止。经试算,z3的齿顶高系数
,直至满足两内啮合副的要求为止。经试算,z3的齿顶高系数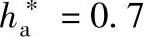 时,满足要求。
时,满足要求。
本例经强度计算,采用模数m=3mm。
其他几何计算与一般少齿差内啮合齿轮副的计算相同。
4.各种形式输出机构的少齿差行星齿轮传动的实测效率
见表9-15~表9-18及图9-59、图9-60。
表9-15 销轴式输出机构的K-H-V(N)型减速器的实测效率
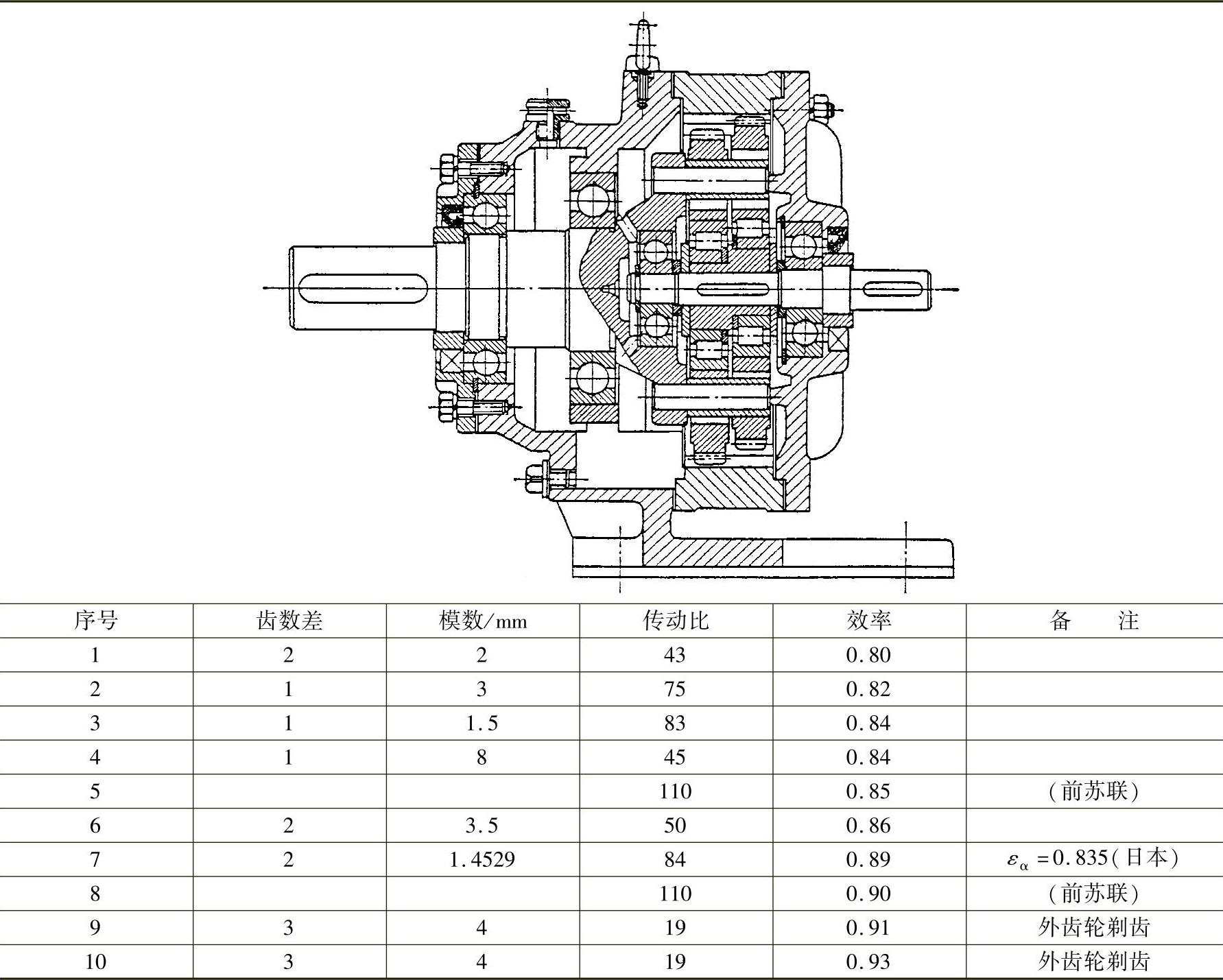
注:表中未加说明的均为我国产品。
表9-16 浮动盘输出机构的K-H-V(N)型减速器的实测效率
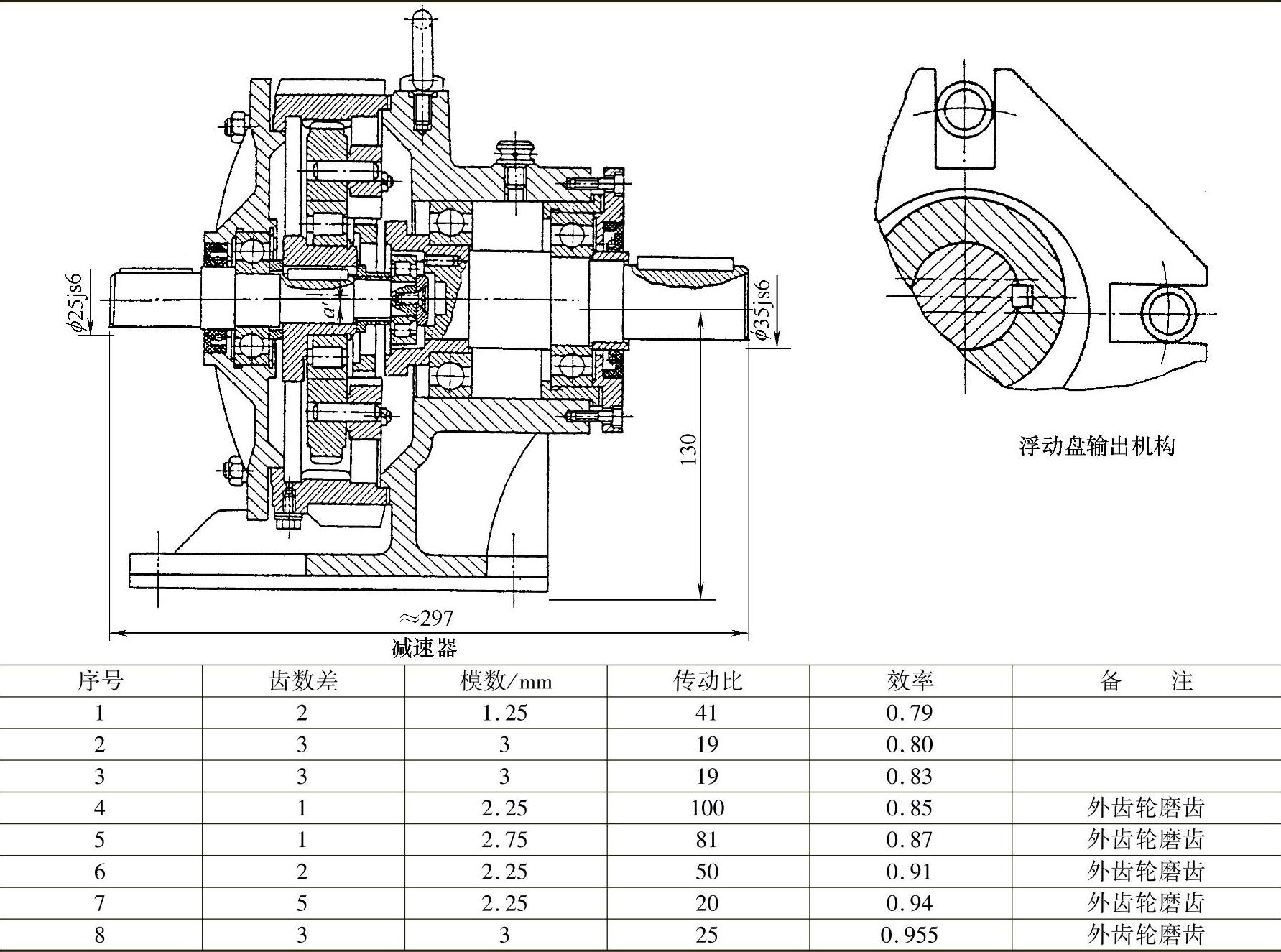
注:1.以上所列均为我国产品,传递功率Pmax=10kW。
2.英国Varatio-Strateline公司的系列产品,功率达36.77kW(50马力)。
表9-17 零齿差输出机构的K-H-V(N)型减速器的实测效率
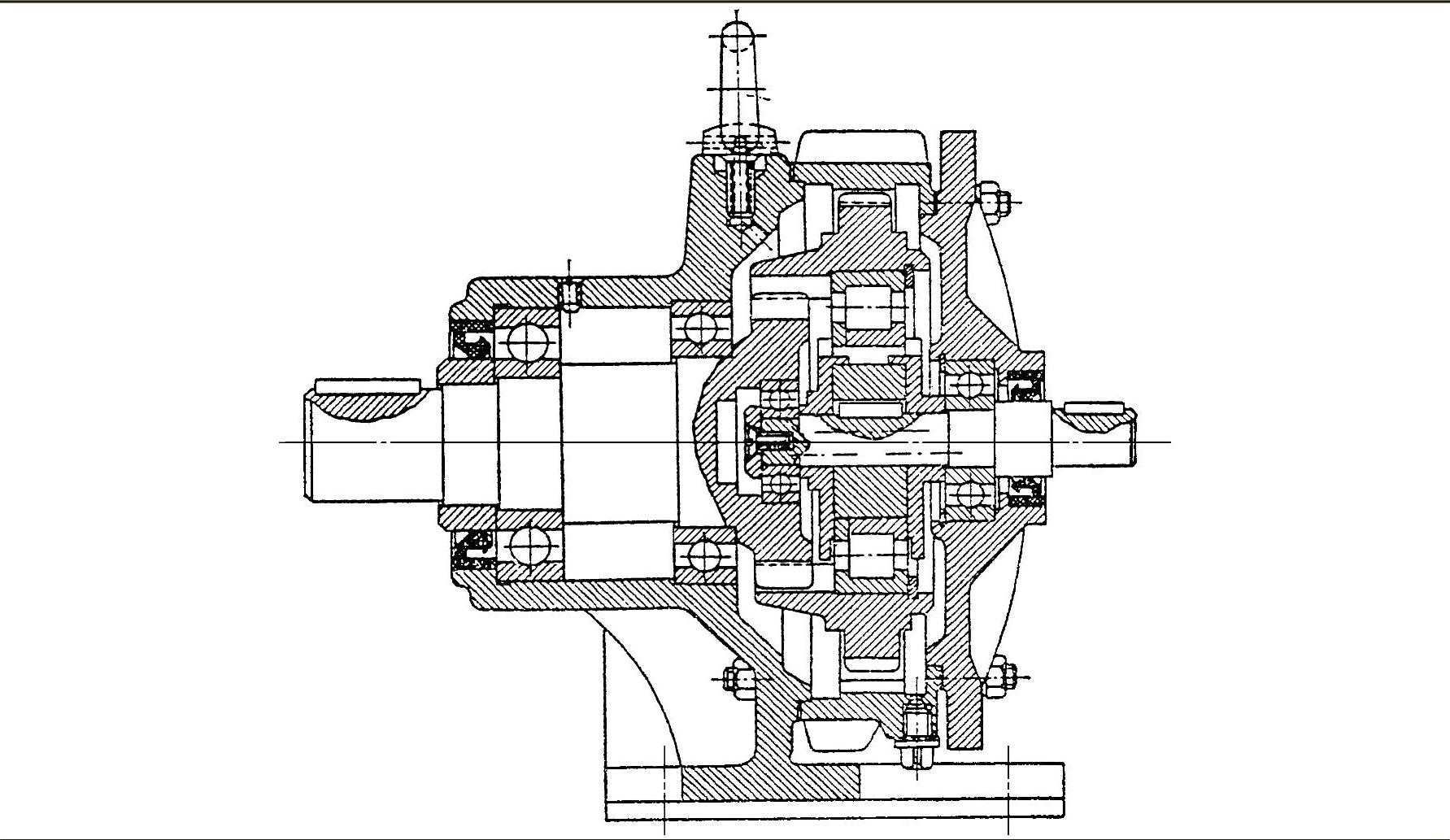
(续)

零齿差输出机构是20世纪70年代才进入实用目前国内外均用于较小的功率场合。阶段的,使用历史最短。其主要优点是加工方便。
表9-18 内齿轮输出的2K-H(NN)型减速器的实测效率
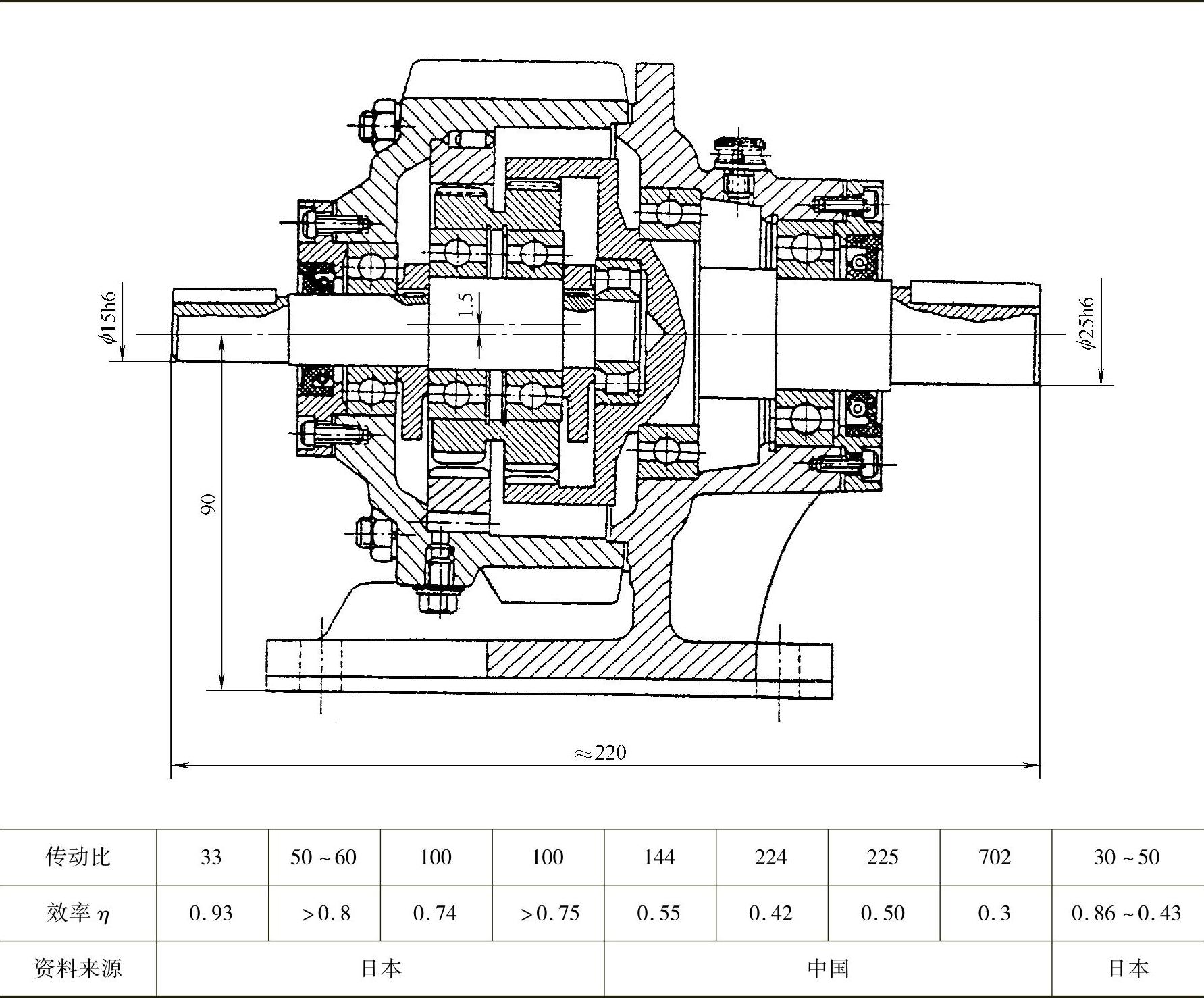
(1)十字滑块式输出机构 这种输出机构采用十字滑块联轴器把行星轮与低速轴连接起来,若是双偏心,还需要把两个行星轮用十字滑块连接,结构如图9-59所示。一般认为这种形式机构的效率低,所以较少采用。事实上也有效率较高的实例。目前国内使用的最大功率为几千瓦,20世纪60年代从日本引进的产品最大功率是11kW。
关于此种形式机构的效率值,介绍甚少。我国有一台传动比i=41的二齿差减速器,实测效率为0.79。日本刊物对此类产品的介绍中报道,效率达0.90左右。若要提高这种形式机构的效率,从滑块的材料选择、加工精度的提高以及形成良好的润滑状态等方面着手,是很有帮助的。
(2)双曲柄式输出机构 用以上4种输出机构组成的传动装置,转臂是高速轴,因此动载荷大。而如图9-60所示的双曲柄式输出机构,高速轴经一级减速后成为转臂的转速,因而减轻了动载荷。总传动比的计算如下式:
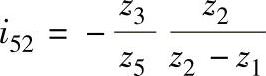
式中,z5及z3分别为第一级普通传动主、从动轮的齿数。
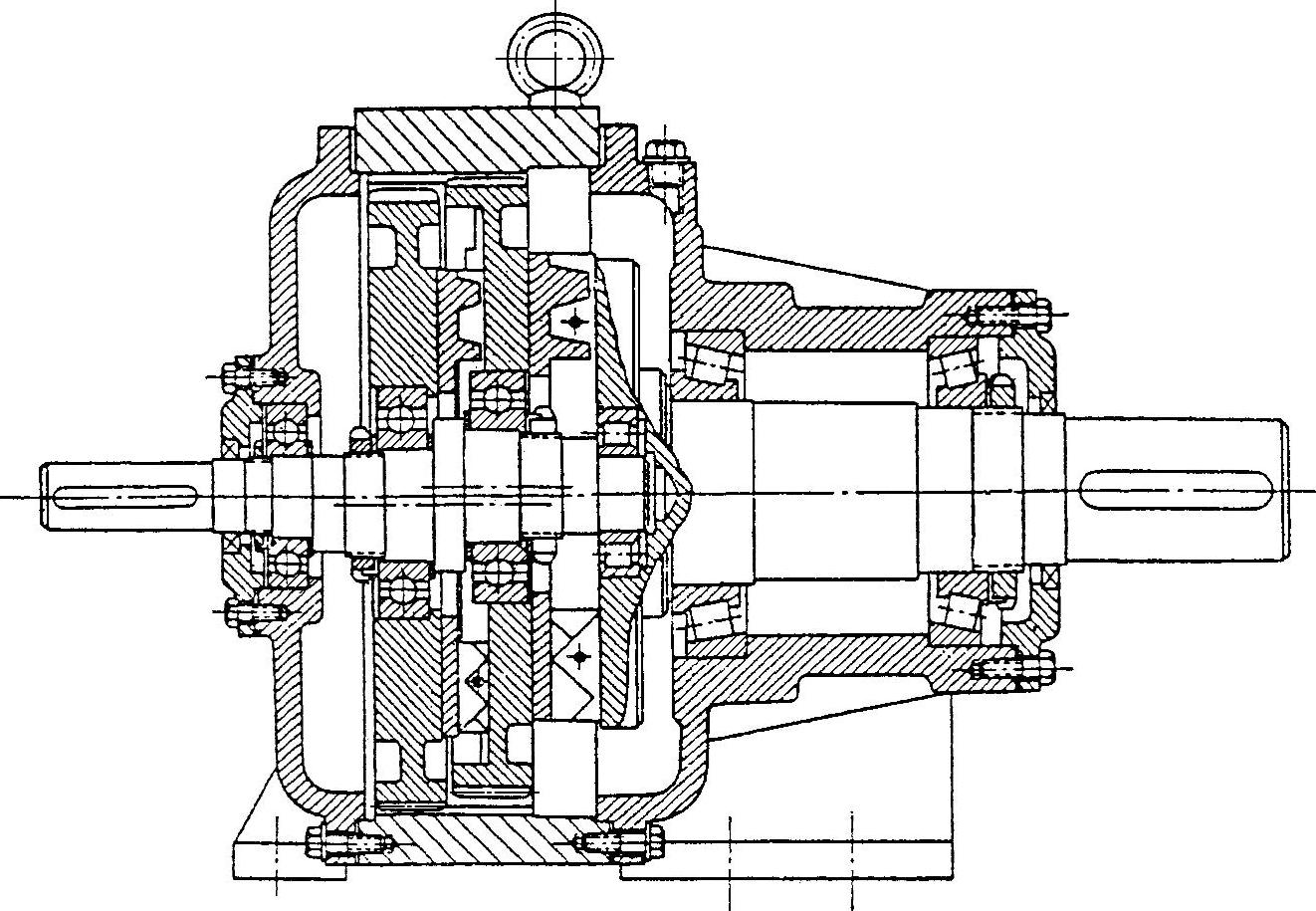
图9-59 用十字滑块输出机构的减速器(上海轻工业设计院)

图9-60 用双曲柄输出机构的少齿差减速器(太原工学院)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




