少齿差行星齿轮传动的强度计算方法

1.受力分析

渐开线少齿差行星传动，其受力情况较为复杂，它不仅与外载荷有关，还与输出机构的形式有关。

（1）销轴式输出机构 取图9-42所示啮合位置的行星轮为分离体，未计及摩擦力，主要承受着三种载荷。

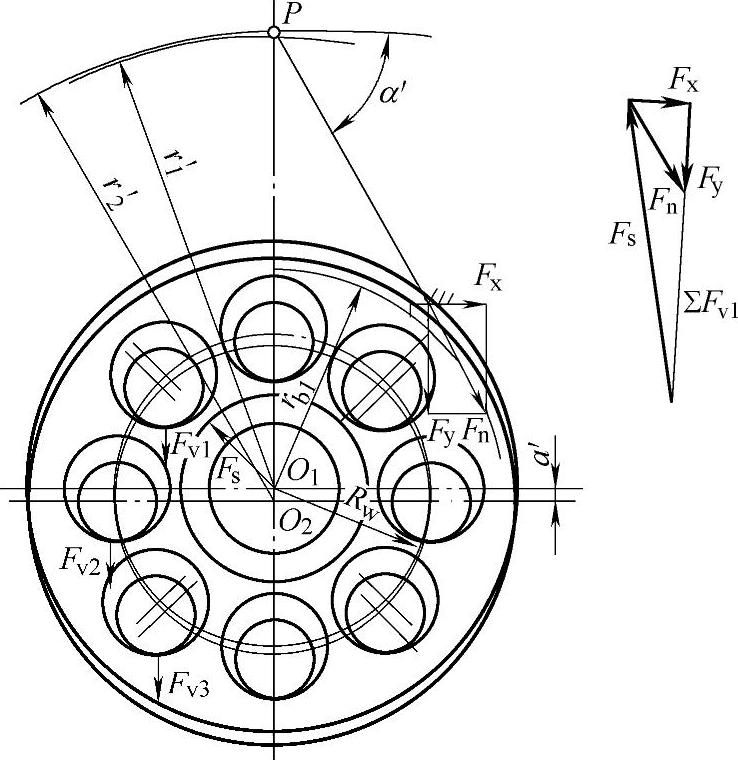
图9-42 行星轮上的受力图

1）内齿圈作用在行星轮上的法向力F_n：

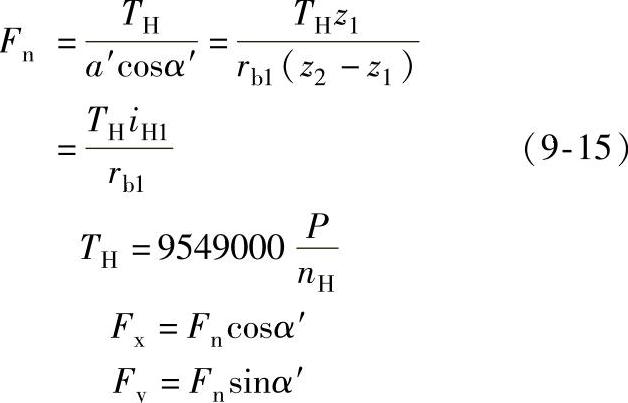
式中 T_H——输入轴转矩（N·mm）；

P——电动机功率（kW）；

n_H——行星架（即偏心轴）转速，即电动机转速（r/min）；

F_n——可沿x方向与y方向进行分解的分力（N）。

2）销轴作用在行星轮上的力F_vi。如图9-43所示，当输出轴开始逆时针方向转动时，销轴对销孔壁的作用力F_vi可通过对节点取矩求得

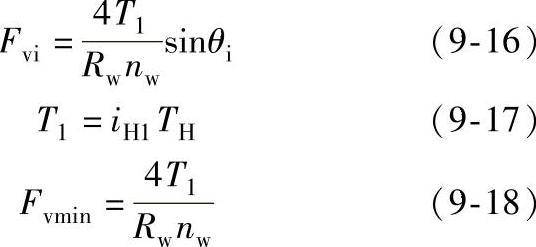
式中 T₁——作用在行星轮上的转矩；

R_w——销孔中心圆半径；

θ_i——销轴与销孔壁接触点和中心O₁连线与y轴夹角；

n_w——销轴数。

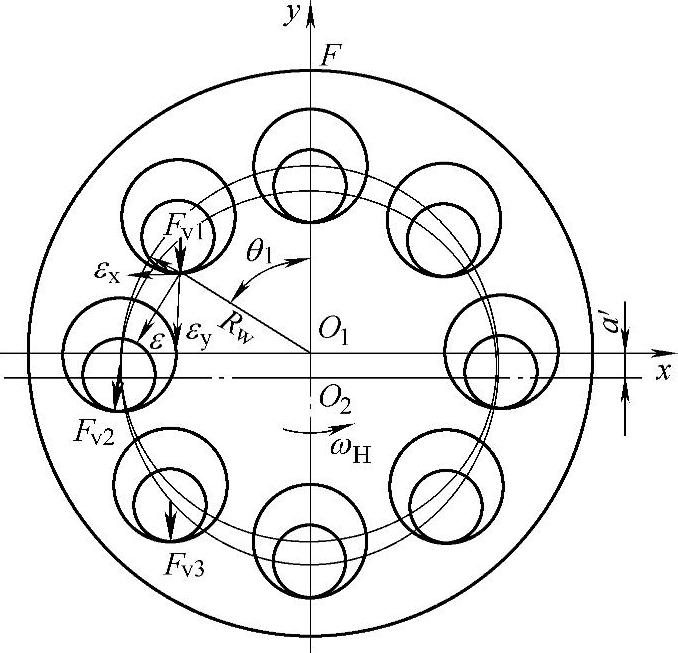
图9-43 计算F_vi简图

图9-43中，ε为应变，ε_x为沿x方向应变，ε_y为沿y方向应变。

3）行星架（即偏心轴）轴承作用在行星轮上的力F_s：

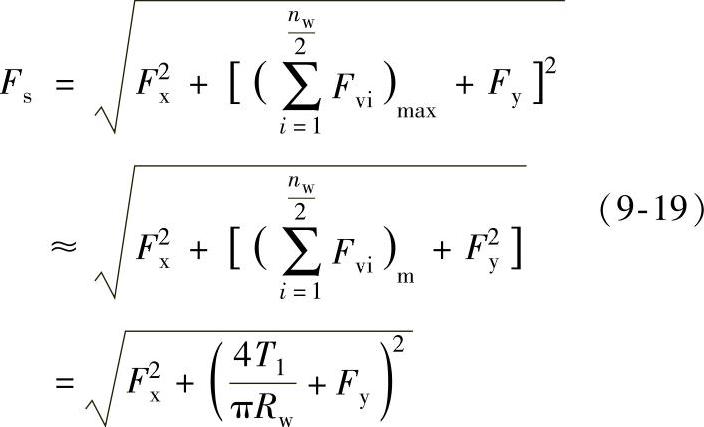
其中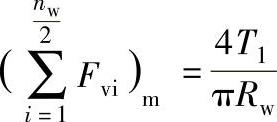，，为F_vi之和的平均值。

（2）浮动盘式输出机构 图9-44为浮动盘式输出机构。将图9-45所示位置的行星轮作为分离体，它也承受三种载荷：内齿圈作用力F_n；浮动盘两滚销作用力F_v；行星架轴承载荷F_s。F_n可由式（9-15）求得，其他如下

F_s=F_n（9-20）

式中 d_w——两滚销之间的距离。

（3）零齿差式输出机构 图9-46所示为零齿差式输出机构受力简图。以图示位置的行星轮为分离体，它也承受着三种载荷：内齿圈作用力F_n；零齿差齿轮的作用力F₀；行星架（偏心轴）轴承载荷F_s。Fn由式（9-15）可求得。

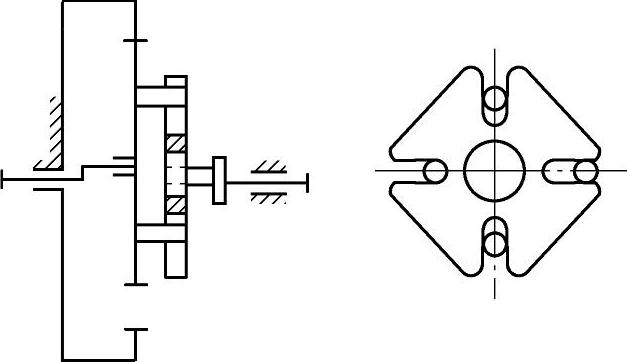
图9-44 浮动盘式输出机构简图

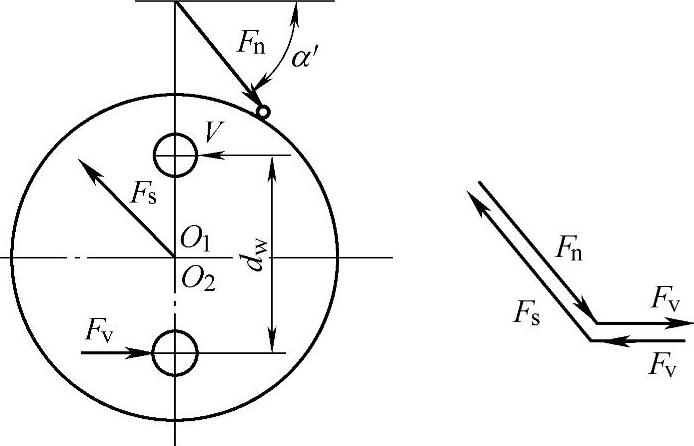
图9-45 行星轮受力简图

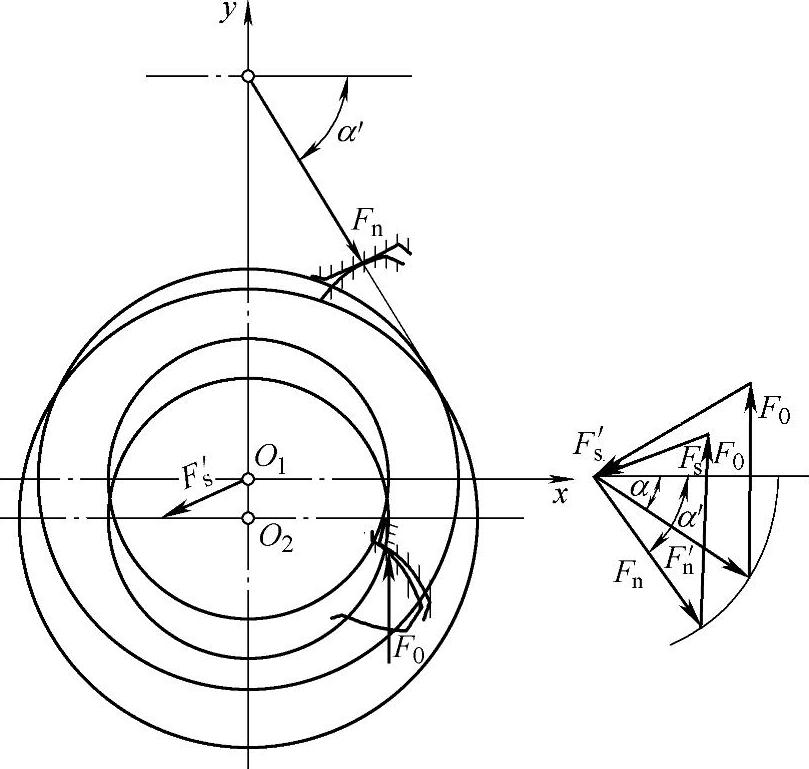
图9-46 零齿差式输出机构受力简图

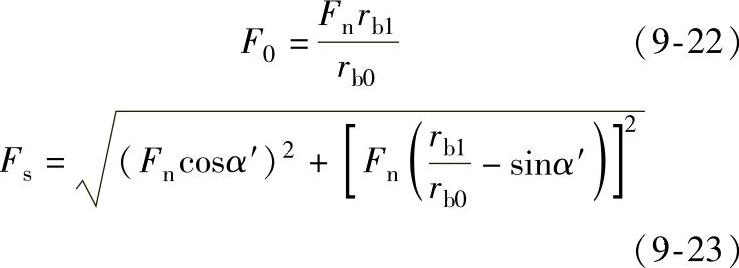
式中 r_b1——少齿差行星轮的基圆半径；

r_b0——零齿差齿轮的基圆半径。

2.主要零件常用材料

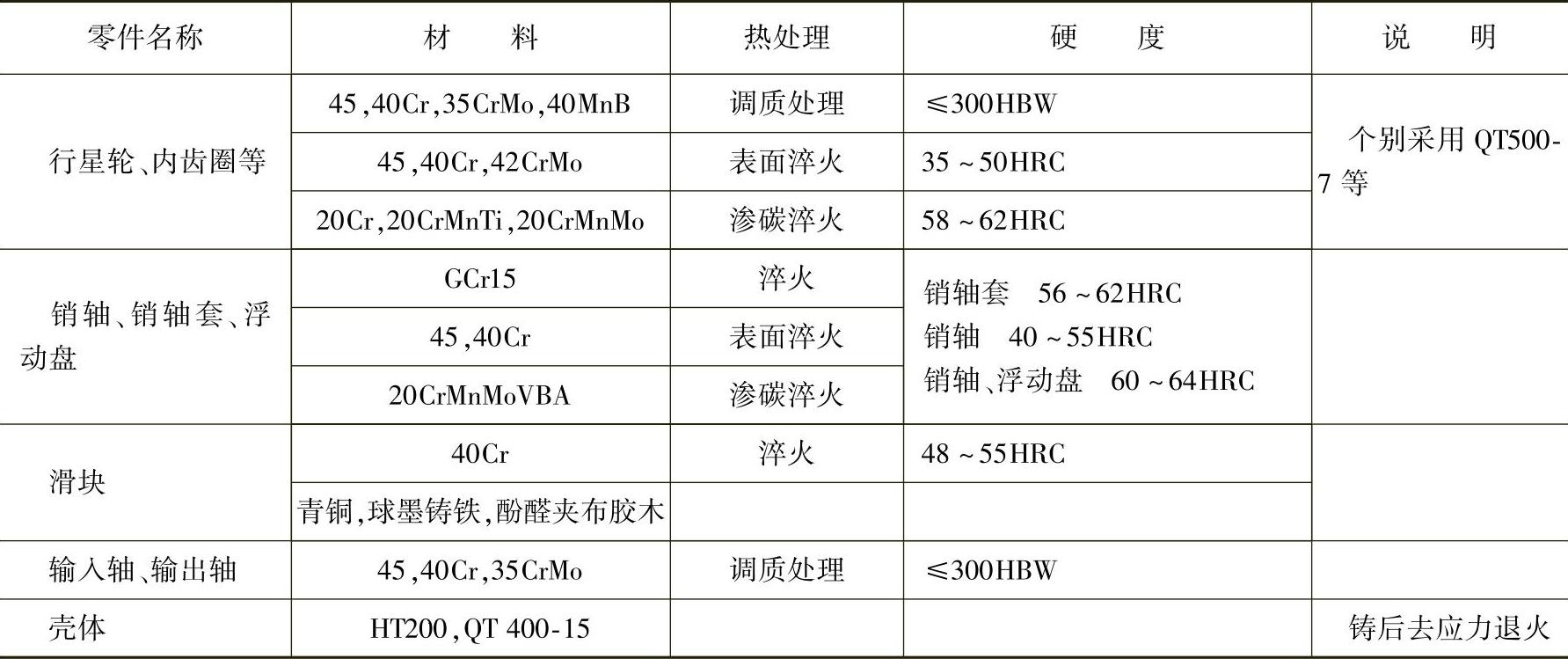
主要零件的常用材料见表9-10。

表9-10 主要零件的常用材料

3.齿轮的强度计算

（1）强度计算式 渐开线少齿差行星齿轮传动为内啮合传动，又采用正角度变位，其齿面接触强度得到较大的提高，与此同时齿根弯曲强度也提高。一般其齿面接触强度安全裕度远高于齿根弯曲强度裕度，所以内啮合的接触强度一般不进行验算。通常只计算齿根弯曲强度，其弯曲强度的条件为

σ_F≤σ_FP（9-24）

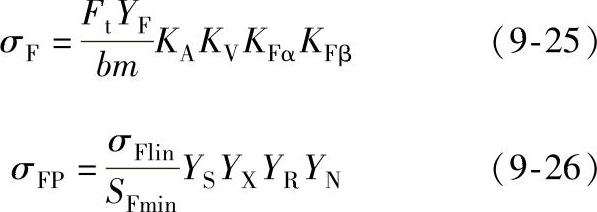
式中 F_t——齿轮分度圆上的圆周力（N）；

Y_F——齿形系数；

K_A——使用系数；

K_V——动载系数；(www.xing528.com)

K_Fα——弯曲强度计算的齿间载荷分配系数；

K_Fβ——弯曲强度计算的齿向载荷分配系数；

σ_Flin——试验齿轮的齿根弯曲极限应力；

S_Fmin——齿根弯曲强度的最小安全系数；

Y_S——应力集中系数；

Y_X——尺寸系数；

Y_R——齿根圆角表面状态系数；

Y_N——弯曲强度的寿命系数。

上述各系数除齿形系数外，可参照有关设计手册确定。

（2）齿形系数

1）少齿差外齿轮齿形系数。少齿差外齿轮的齿形系数按30°切线法确定轮齿危险截面位置进行计算，计算公式为

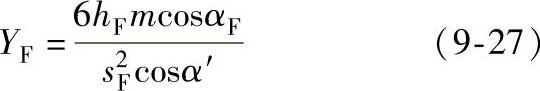
式中 h_F——法向力的作用线与轮齿中心线交点至危险截面的距离，见图9-47；

s_F——危险截面的厚度；

α_F——法向力的作用线与两切点连线的夹角。

Y_F也可直接查线图取得，图9-48与图9-49分别为齿顶高系数h_a∗=0.75与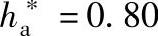的齿形系数线图。

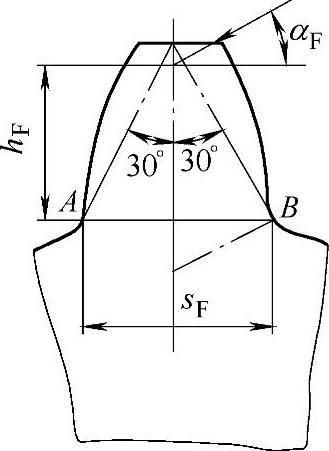
图9-47 外齿轮齿形系数计算图

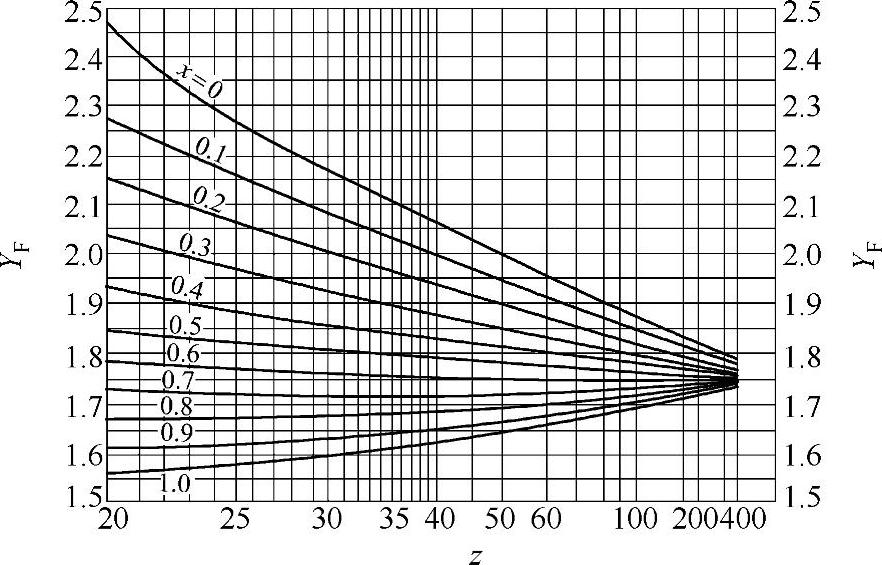
图9-48 齿形系数Y_F（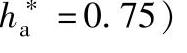

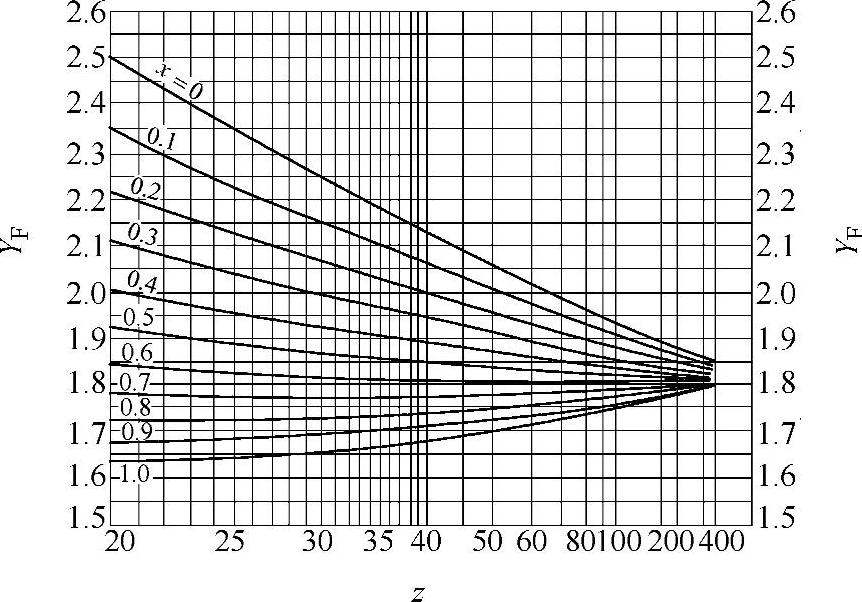
图9-49 齿形系数Y_F（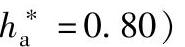

对于零齿差外齿轮的齿形系数，因它具有切向变位，在无现成资料时，其参数h_F、s_F与α_F可通过作图法量得，然后按式（9-27）计算。

2）少齿差内齿圈齿形系数。内齿圈齿形系数的计算资料较少，少齿差传动更少。内齿圈由于弯曲强度不够而失效的概率甚低，甚至于不必进行校核计算。若内齿圈重要时，一定要校核，可采用作图法求得齿形系数。

对于内齿圈用30°切线法确定危险截面不甚合理，经有限元计算及光弹试验验证，可按55°切线法确定轮齿的危险截面，以此作为近似作图法的依据。作图法的步骤如下（见图9-50）：

①计算内齿圈分度圆上的齿厚s2

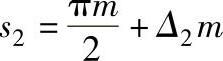
Δ₂=（z₂-z₁）（invα-invα′）-Δ₁Δ₂为负值，其他符号同前。

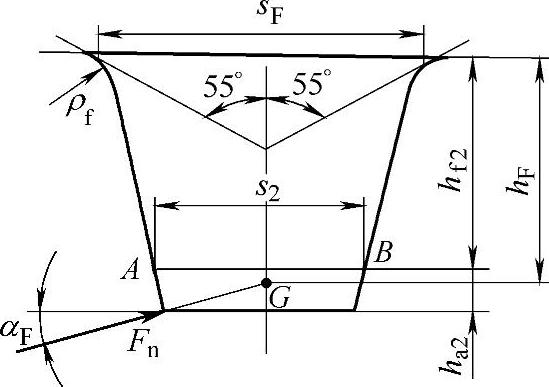
图9-50 内齿圈齿形系数作图法

②作齿条中线，在中线上截取。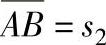

③过点A和B作齿条的齿形。

④作齿条的齿顶线与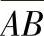相平行，其距离h_a2=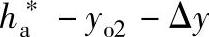（）m。

⑤作齿条的齿根线与AB相平行，其距离h_f2=（h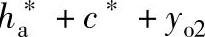）m。

⑥作齿根处圆角，取圆角半径ρ_f=0.38m。

⑦相对于轮齿中心线作55°的直线与齿根圆角相切，在两切点间连一直线，其长度为s_F。

⑧过齿顶沿与齿顶线夹角α_F方向作齿面的法线，与轮齿中心线交于G点，则在图上量取h_F值。

⑨用式（9-27）计算齿形系数Y_F。

4.输出机构的强度计算

输出机构的强度计算见表9-11。

表9-11 输出机构的强度计算

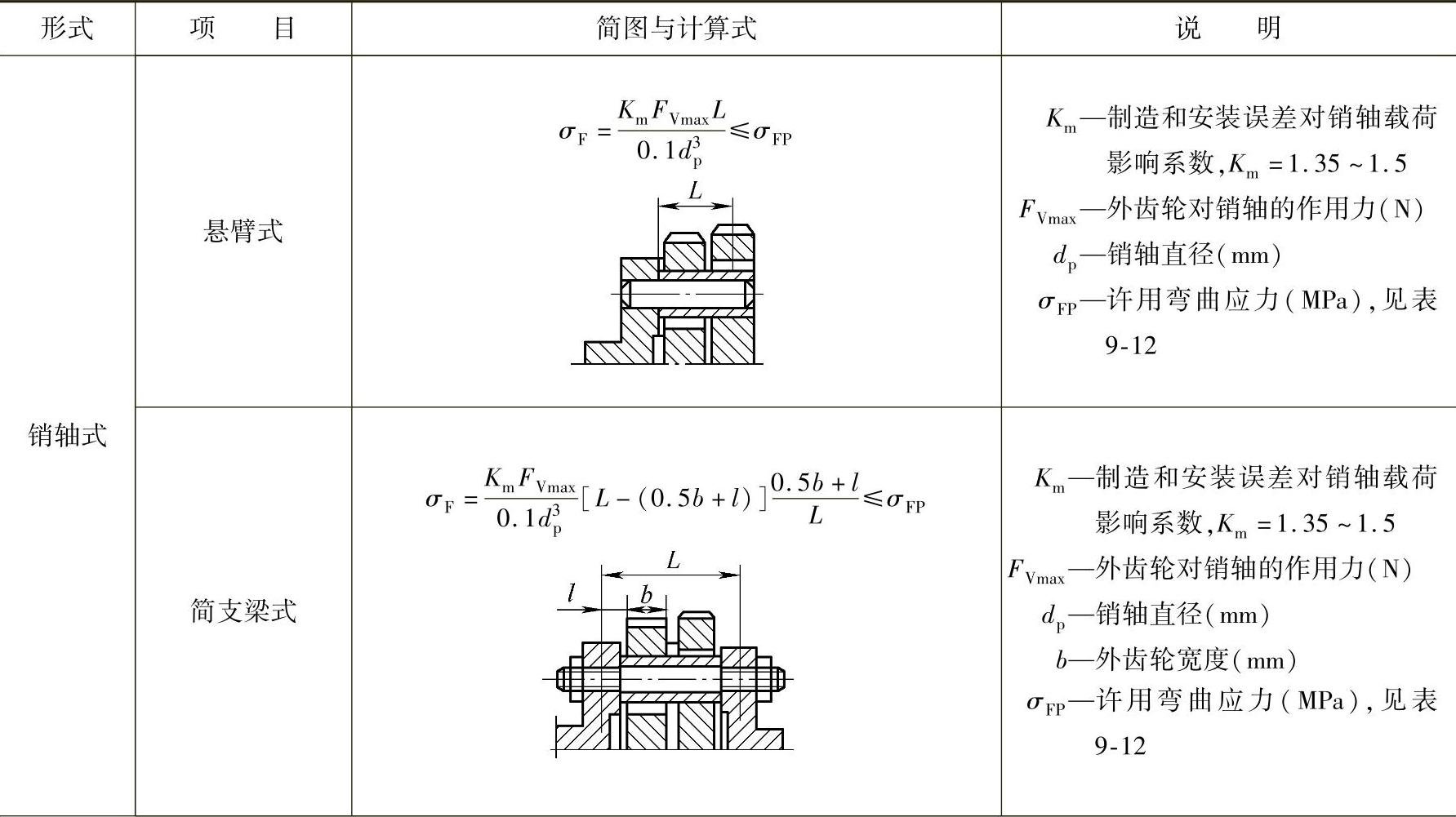
（续）

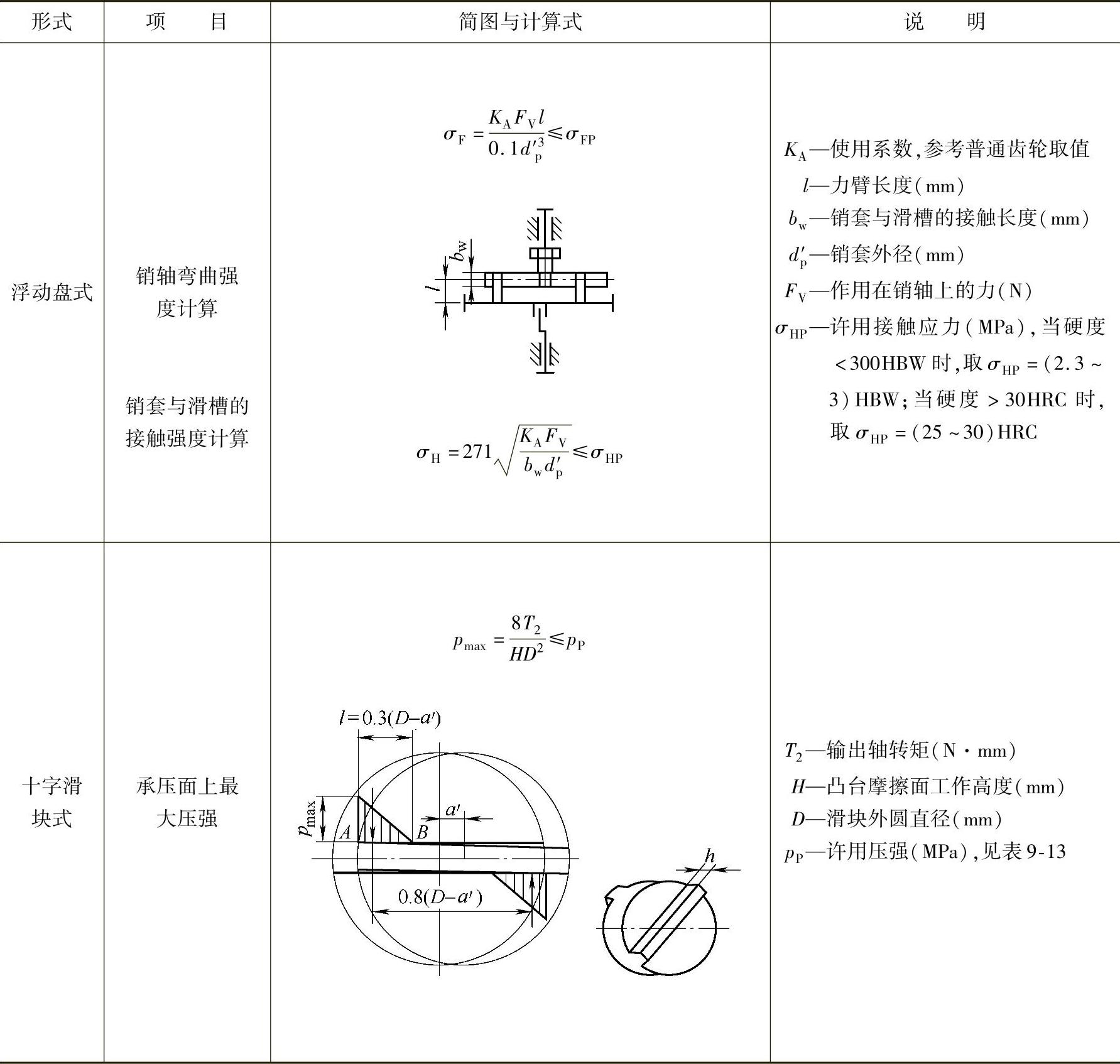
表9-12 销轴的许用弯曲应力σFP

表9-13 许用压强p_P （单位：MPa）