零齿差内齿轮副可以作为一种输出机构形式(见图9-6),它可使输出机构简化,便于加工制造。
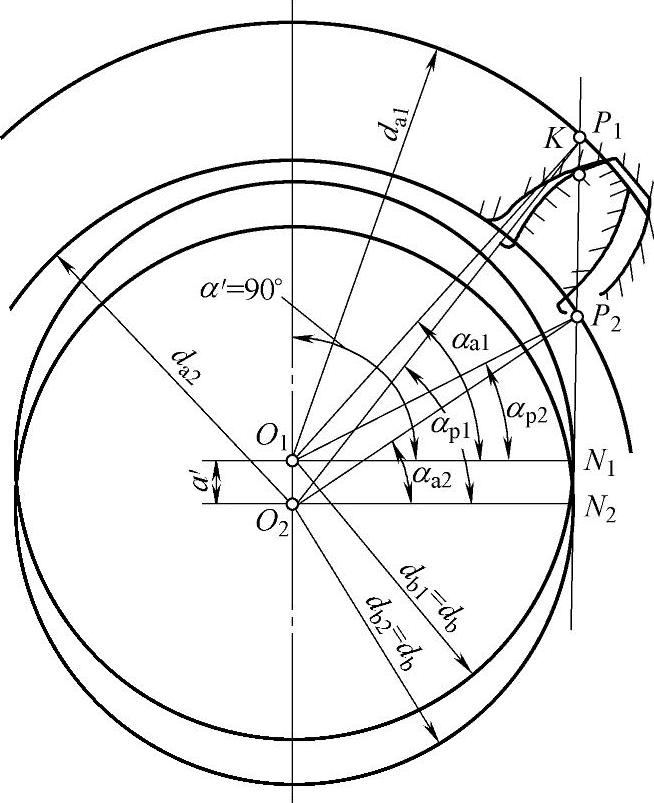
图9-34 零齿差内齿轮副的几何关系
其特点是内、外齿轮齿数相同,且传动比为1,类似于齿轮联轴器,但齿轮联轴器内外齿轮的中心距为零。而零齿差内齿轮副的内、外齿轮的中心距大于零,如图9-34所示。为了保证正常安装与运转,需要较大的齿侧间隙,仅仅采用径向变位不能满足要求,需要同时采用径向变位与切向变位,使内齿圈的齿槽增大,外齿轮的齿厚变薄,以获得较大的齿侧间隙。
1.零齿差内齿轮副的啮合方程式
由于内齿轮副两齿轮的模数与齿数相同,因此两基圆相同,节圆为无限大,啮合角α′=90°,其啮合方程式为
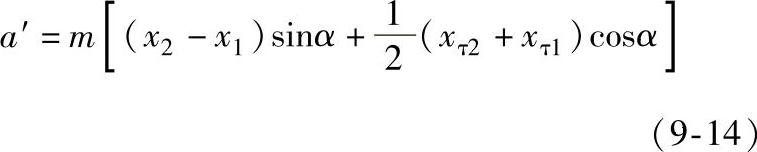
式中 x1——外齿轮的径向变位系数;
x2——内齿圈的径向变位系数;
xτ1、xτ2——外齿轮与内齿圈的切向变位系数;
α——压力角。
2.零齿差内齿轮副的主要几何限制条件(见表9-4)
表9-4 零齿差内齿轮副的主要几何限制条件

(续)

3.确定变位系数的方法
为避免径向干涉,内齿圈应径向正变位,可参照表9-5选取x2。取定x2后,从啮合方程可知,还有三个变位系数x1、xτ1、xτ2待定,这三个参数的确定可用下述两种方法:
1)试取(xτ1+xτ2),代入啮合方程求得相应的x1,然后验算外齿轮的根切,计算几何尺寸,验算重合度εα和齿顶厚系数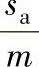 ,通常取(xτ1+xτ2)不小于-1。
,通常取(xτ1+xτ2)不小于-1。
2)按外齿轮不产生根切的条件取x1,代入啮合方程求得(xτ1+xτ2),然后计算几何尺寸与验算重合度εα和齿顶厚系数,为不使外齿轮根部强度太弱,一般取x1为正值。
表9-5 插削内齿轮时齿轮的最少齿数限制
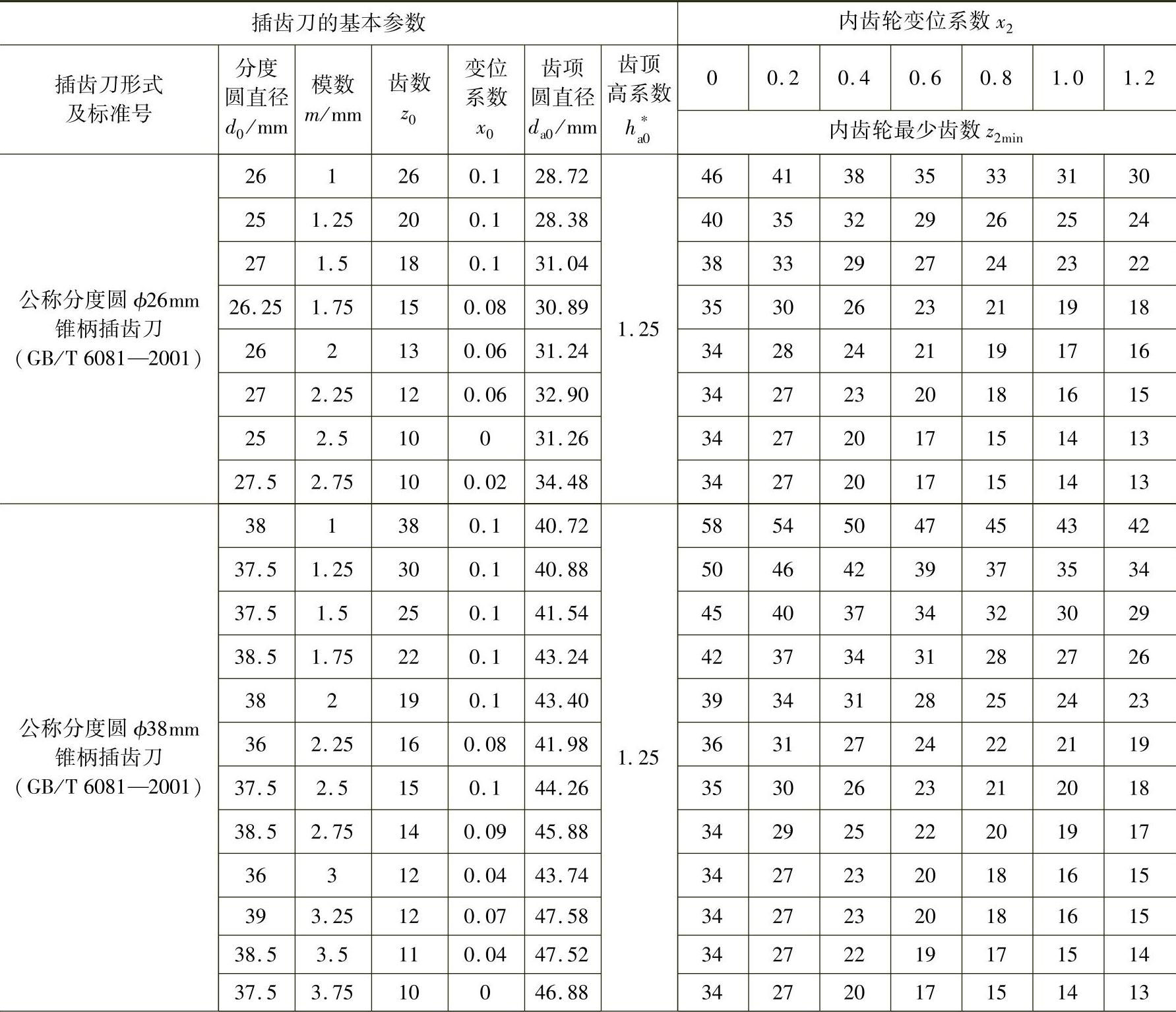
(续)
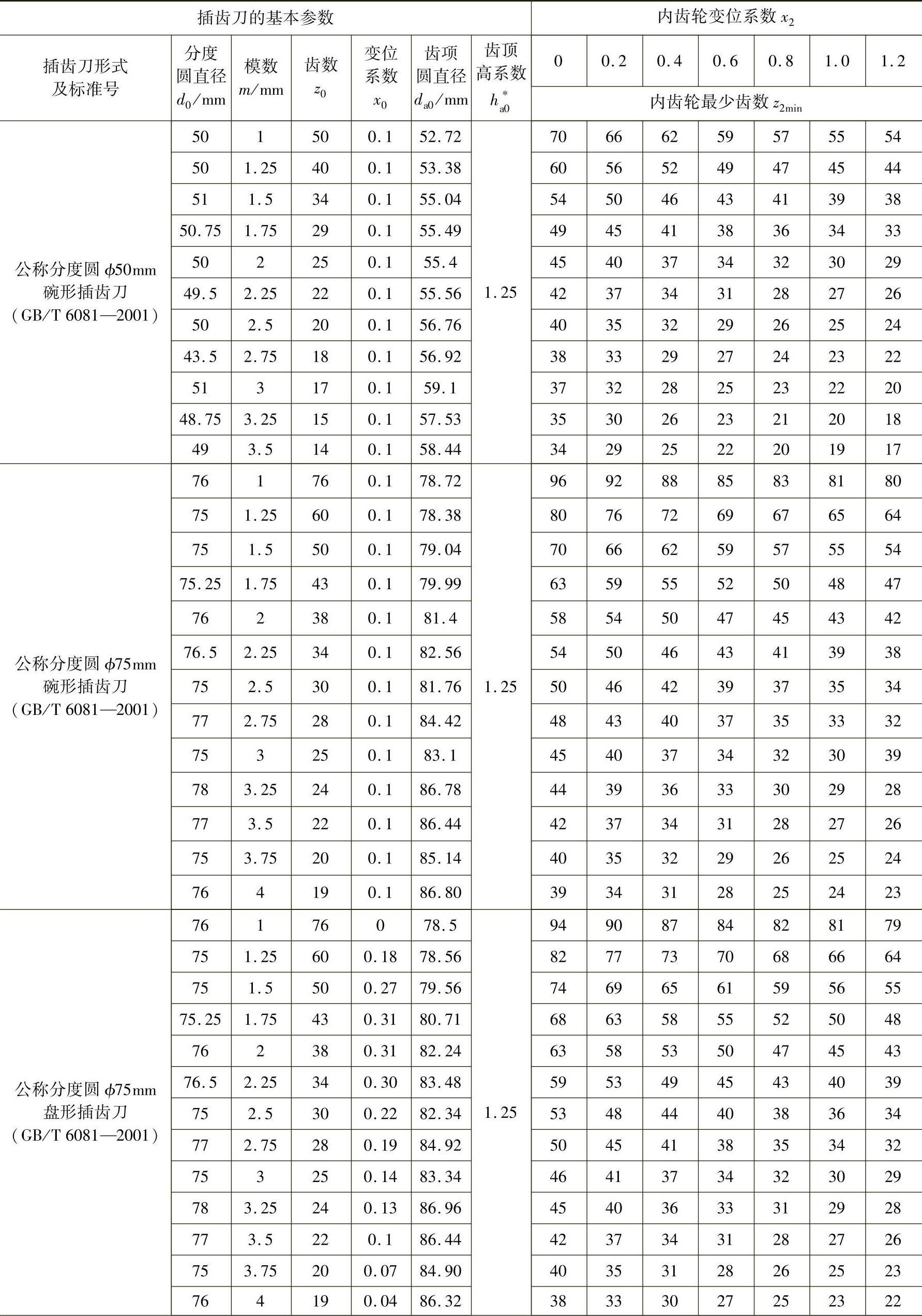
(续)
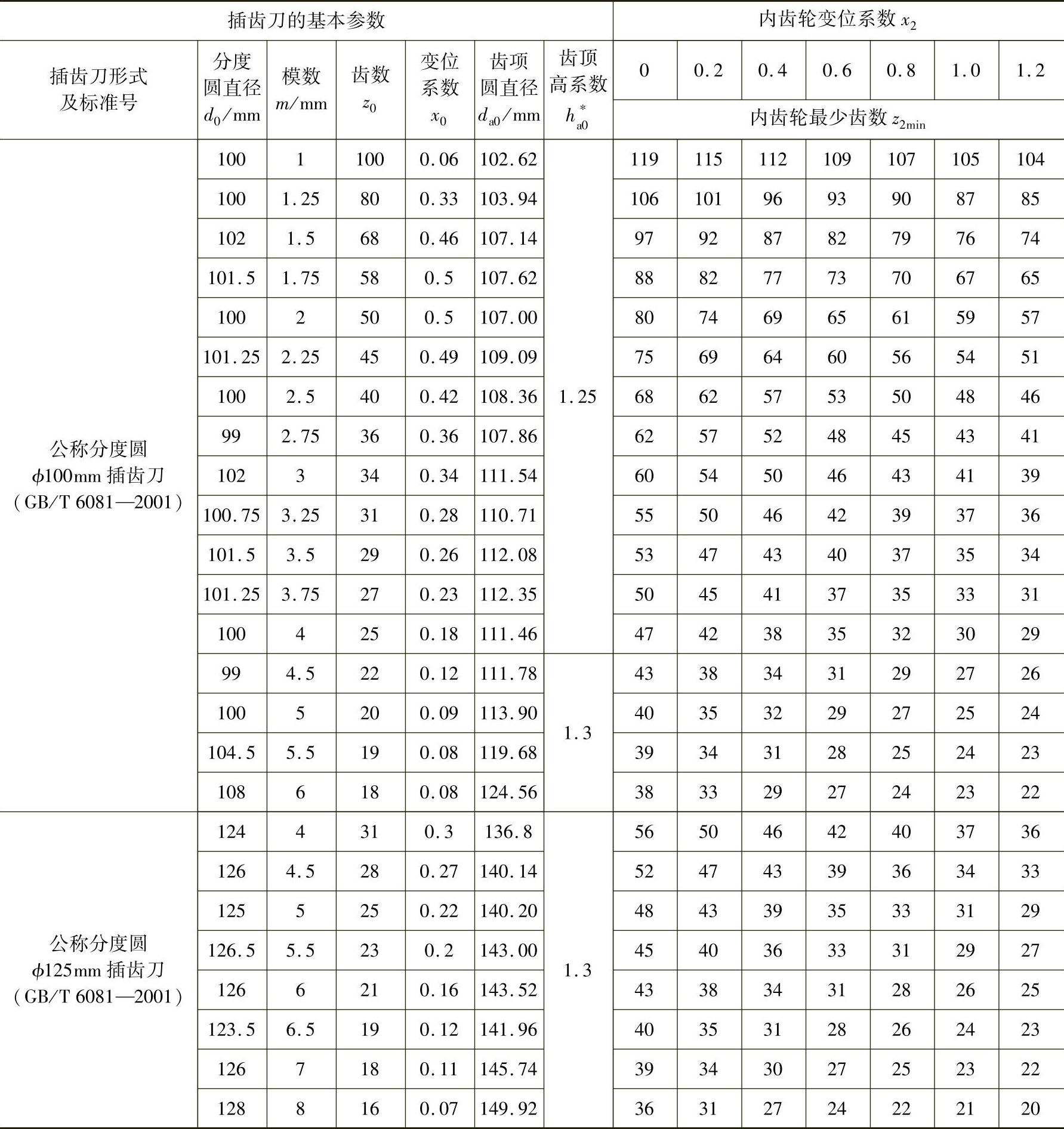
注:1.表列z2min适用于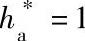 和α=20°的情况。若
和α=20°的情况。若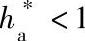 ,则z2min也小于表列数值。
,则z2min也小于表列数值。
2.当插齿刀前面刃磨,即x0小于表列数值时,z2min也小于表列数值。
3.对于表中没有列出的其他直径的插齿刀,可参照与表中的z0和x0相同的数值来确定z2min。
在验算过程中,如εα<1.10时,则应增大x1,重新计算和验算,一般先验算εα,再验算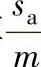 。(xτ1+xτ2)取定后的分配,可先试取xτ1和xτ2,并分别计算
。(xτ1+xτ2)取定后的分配,可先试取xτ1和xτ2,并分别计算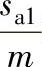 和
和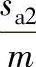 ,使它们接近便可。
,使它们接近便可。
此外,零齿差内啮合传动的径向变位系数也可由封闭图确定,然后再确定xτ1、xτ2,如图9-35所示。对于封闭图的绘制,其中外齿轮z1用滚刀加工,内齿圈z2用插齿刀加工。在选取变位系数时,按图9-36~图9-40的封闭图,根据z和z0选取合理的变位系数。图9-41为零齿差内啮合齿轮副。
零齿差z∑=z2-z1=0内啮合齿轮副的封闭图由下列限制曲线组成(见图9-35):
1——重合度εα=1的限制曲线;
2——齿顶厚sa1=0的限制曲线;
3——齿顶厚sa2=0的限制曲线(图中未示出);
4——齿轮z2纵向齿顶与齿轮z1齿根过渡曲面干涉的限制曲线;
5——齿轮z1纵向齿顶与齿轮z2齿根过渡曲面干涉的限制曲线;
6——齿轮z2与插齿刀齿根过渡曲面产生顶切干涉的限制曲线;
7——齿高h=h0=2.5m的限制曲线;
8——啮合角α′=0的限制曲线;
9——重合度εα=1.2的限制曲线;(https://www.xing528.com)
10——齿顶厚sa1=0.25m的限制曲线。
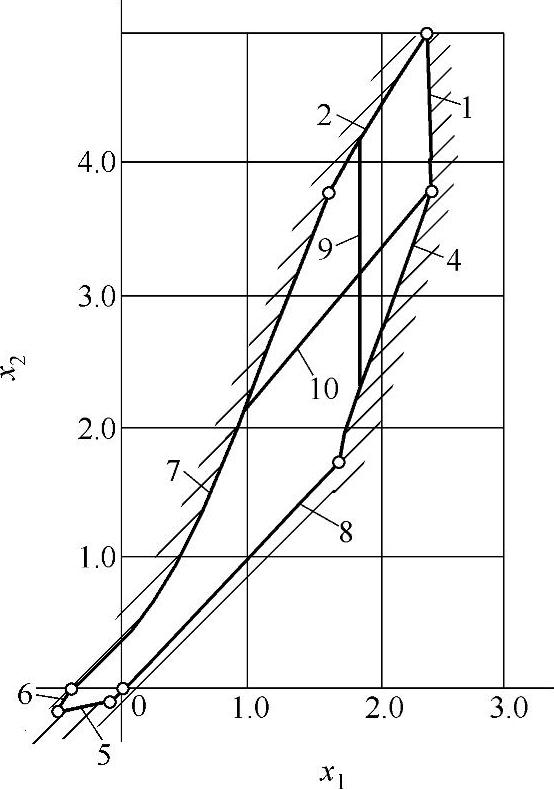
图9-35 零齿差z∑=z2-z1=0内啮合齿轮副封闭图
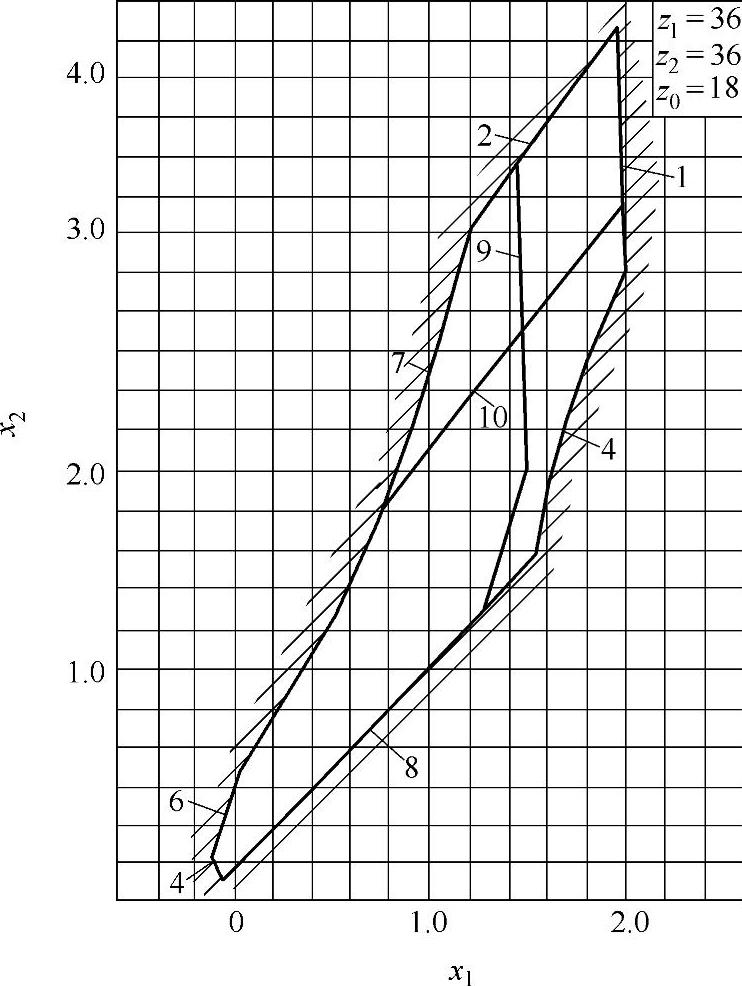
图9-36 变位系数封闭图(一)
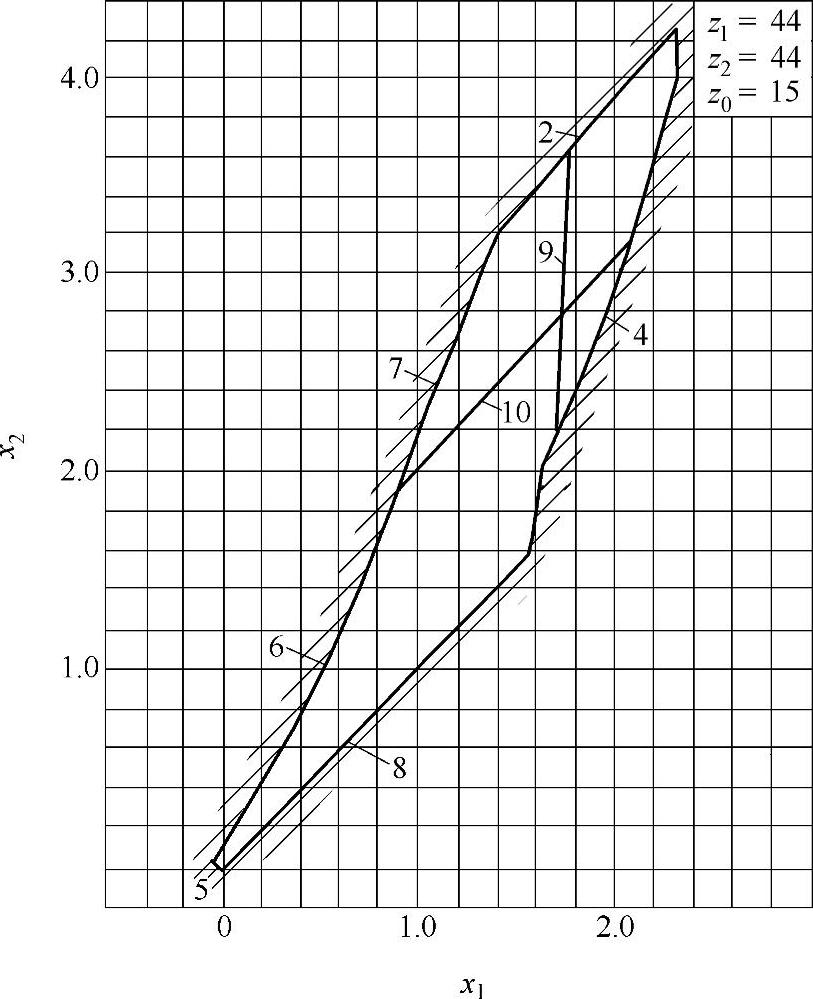
图9-37 变位系数封闭图(二)
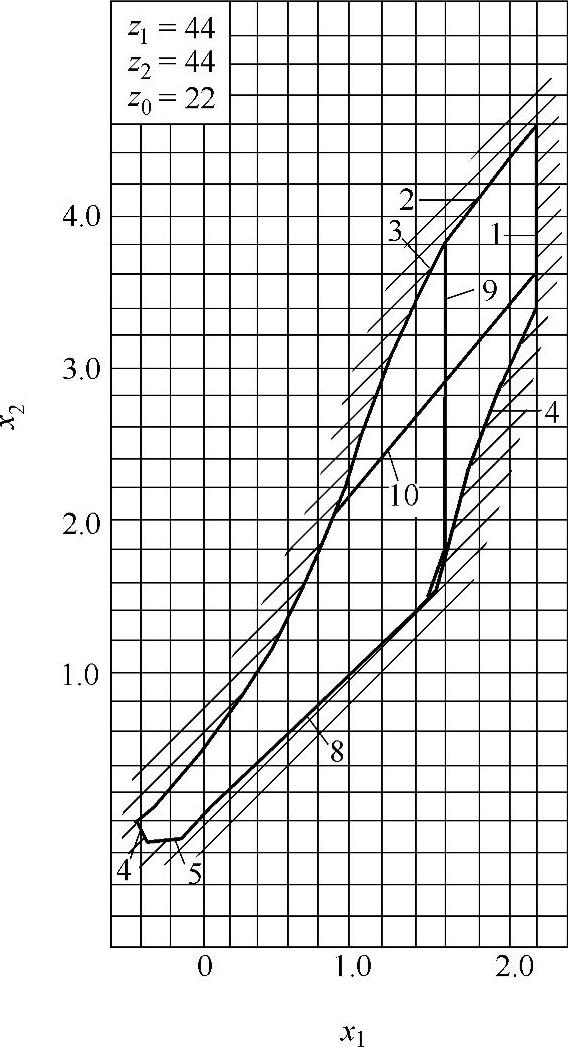
图9-38 变位系数封闭图(三)
4.零齿差内啮合齿轮副几何计算实例
已知一零齿差内啮合齿轮副,中心距a′=0.84mm,模数m=2mm,齿形角α=20°,齿顶高系数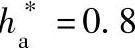 ,齿数z1=z2=z=20。
,齿数z1=z2=z=20。
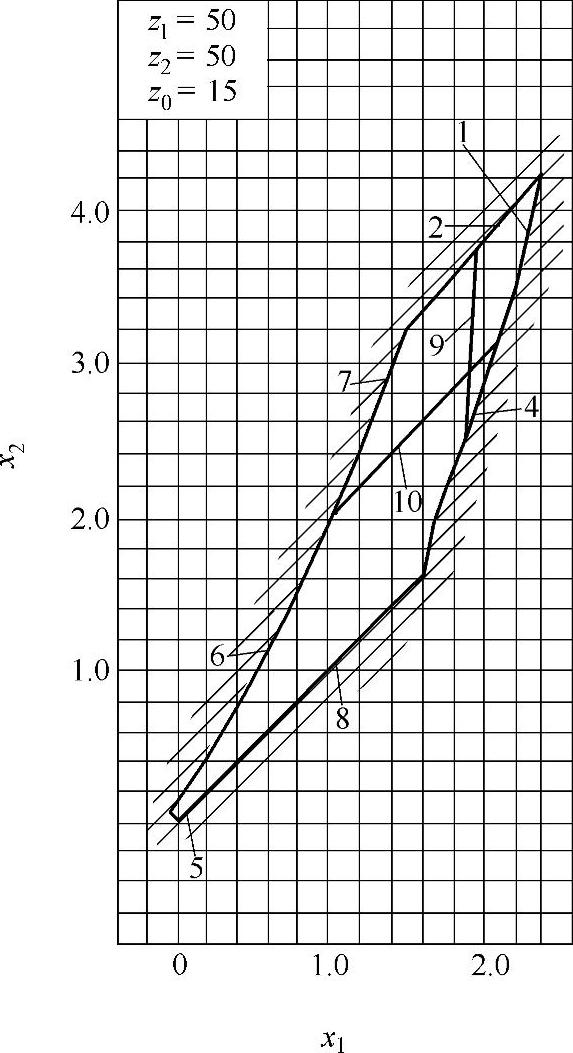
图9-39 变位系数封闭图(四)
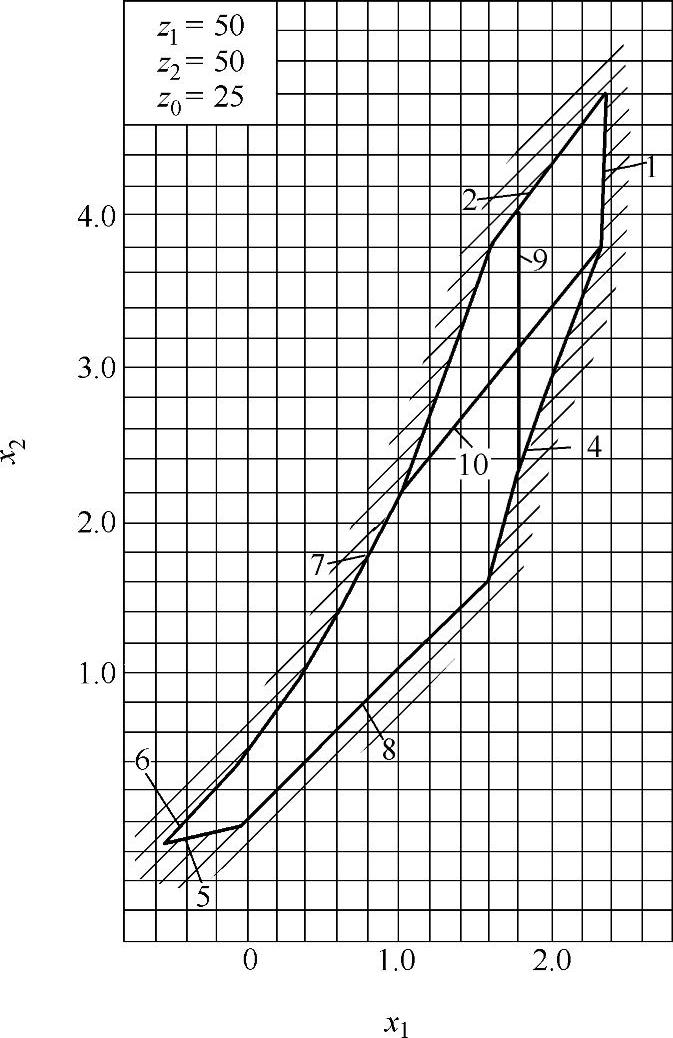
图9-40 变位系数封闭图(五)
1)根据m=2mm,α=20°,选用插齿刀z0=13,插齿刀齿顶高系数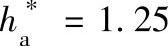 ,锥柄插齿刀(GB/T 6081—2001)。
,锥柄插齿刀(GB/T 6081—2001)。
2)由表9-5选取x2,新刀时应取x2=0.7(这是系数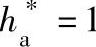 的情况,对于
的情况,对于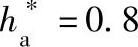 时,则更偏于安全,更不会产生退刀干涉)。
时,则更偏于安全,更不会产生退刀干涉)。
3)试取外齿轮变位系数x1。
①试取x1=0,xτ1+xτ2=-0.38435,以此进行几何计算,并计算重合度εα=0.89<1,偏小。
②试取x1>0的数值:
x1=0.2时,则得εα=1.02;
x1=0.4时,则得εα=1.15,取x1=0.4。
③确定响应的xτ1+xτ2,由啮合方程得
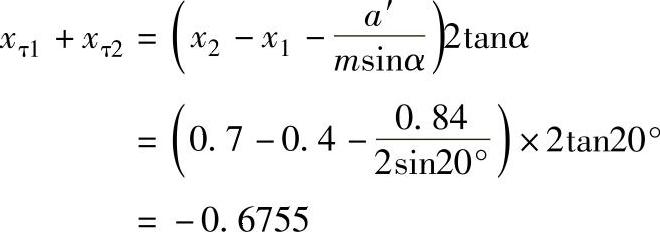
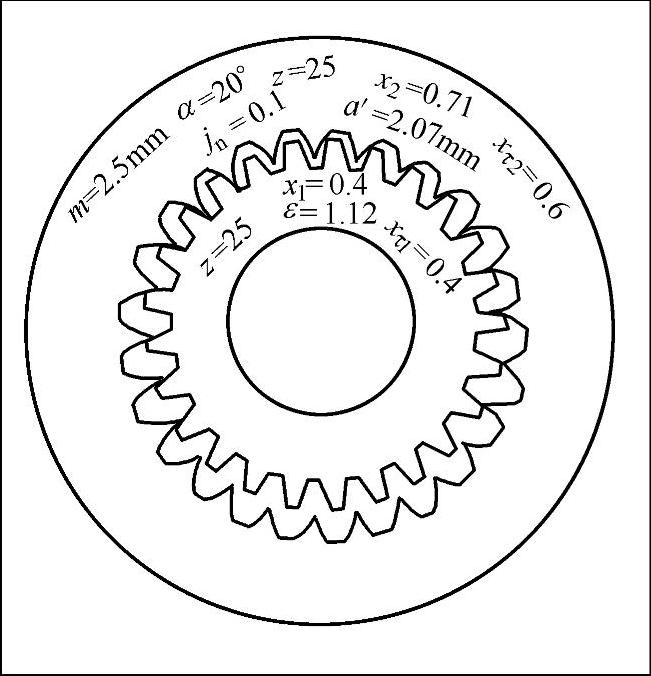
图9-41 零齿差内啮合齿轮副
④若取xτ1=-0.3755,xτ2=-0.3,则计算得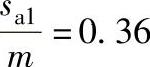 ,
,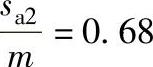 ,两者相差甚大,于是重新取xτ1和xτ2,最后决定xτ1=-0.2255,xτ2=-0.45。
,两者相差甚大,于是重新取xτ1和xτ2,最后决定xτ1=-0.2255,xτ2=-0.45。
4)几何尺寸计算。
分度圆直径
d=d1=d2=mz=2×20mm=40mm
基圆直径
db=db1=db2=dcosα=40×cos20°mm=37.5877mm齿顶高
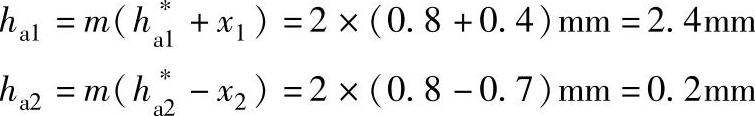
齿顶圆直径
da1=d1+2ha1=(40+2×2.4)mm=44.8mm
da2=d2+2ha2=(40-2×0.2)mm=39.6mm>db2
所以内齿圈齿顶部分是渐开线。
5)重合度计算εα=1.151。
6)齿顶厚系数验算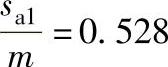 ,
,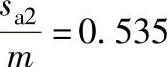 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




