内啮合齿轮副干涉及变位系数优化选取

1.少齿差内啮合齿轮副的干涉

由于渐开线少齿差内啮合齿轮副的内、外齿轮仅相差1、2齿或3、4齿，若采用标准齿轮就不能进行正常的啮合传动，将会产生各种干涉现象。

1）切齿加工时的顶切与根切。

①用插齿刀插制内齿圈时产生的顶切。

②用插齿刀插制外齿轮时产生的顶切。

③用滚刀加工外齿轮时产生的根切。

2）过渡曲线干涉。

①内齿圈齿顶与插制外齿轮根部的过渡曲线干涉。

②内齿圈齿顶与滚切外齿轮根部的过渡曲线干涉。

3）内齿圈齿顶部分为非渐开线。

4）节点对面的齿顶干涉。

5）齿廓重叠干涉。

6）内外齿轮沿径向移动发生的径向干涉。

此外，为了保证传动的平稳性，应要求重合度ε_α＞1。

2.变位系数的选择

确定变位系数时，首先应满足内啮合的啮合方程式：

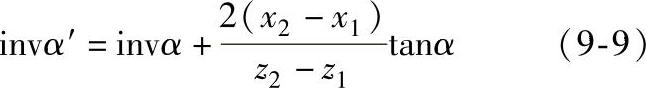
由上式可知，当齿轮的齿数z₂、z₁和齿形角α为已知时，变位系数x是啮合角α′的函数。

变位系数选择时，还应满足多项内啮合的几何限制条件，但其中最主要的是满足如下两个条件：

1）齿轮副的重合度ε_α＞1，即应符合以下不等式

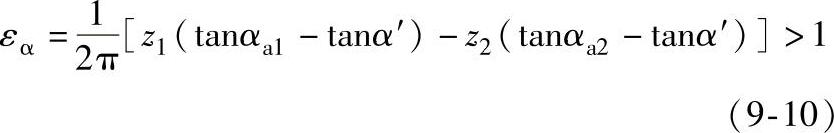
2）不产生齿廓重叠干涉，即应满足如下不等式G_s=z₁（δ₁+invα_a1）-z₂（δ₂+invα_a2）+（z₂-z₁）invα′＞0（9-11）

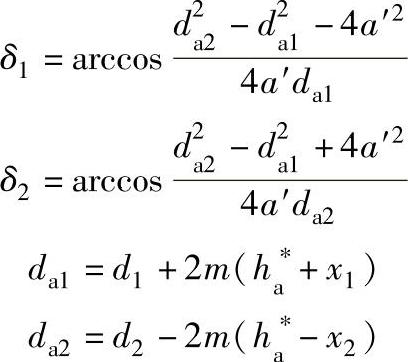
式中 d_a1——行星轮齿顶圆直径；

α_a1——行星轮齿顶圆压力角；

d_a2——内齿圈齿顶圆直径；

α_a2——内齿圈齿顶圆压力角；

a′——齿轮副啮合中心距。

为了满足ε_α和G_s两个不等式，应先按重合度的预期值[ε_α]，用迭代法计算变位系数。在α′不变时，迭代程序如下

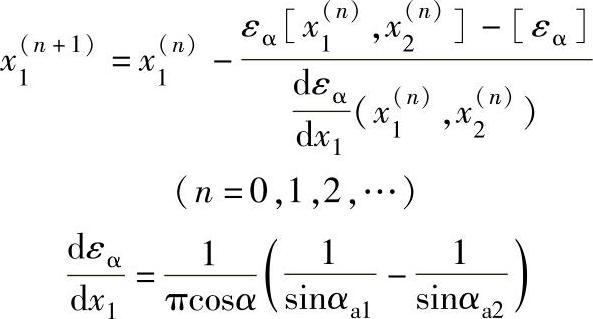
式中 [ε_α]——ε_α的预期值，根据对传动运转性能的要求确定。

求得x₁和x₂后，用此值验算齿廓重叠干涉，若不满足条件，则增大a′（即增大x）值重新计算。

或者，按齿廓重叠干涉预期值[G_s]用迭代法计算变位系数。在α′不变时，迭代程序如下

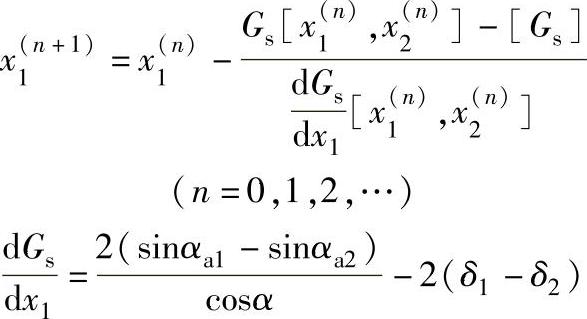
式中 [G_s]——G_s的预期值，一般取[G_s]≈0.05。

求得x₁和x₂后，用此值验算重合度，若不满足条件，则减小a′（即减小x）值重新计算。总之上述两项条件必须同时满足。

此外，还可以用封闭图来选择变位系数，对于z∑=z₂-z₁=1的少齿差内啮合传动的封闭图，如图9-17～图9-32所示。

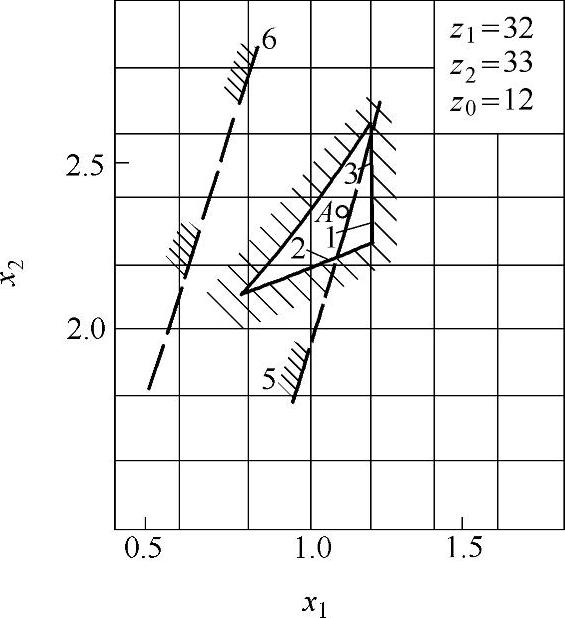
图9-17 变位系数封闭图（一）

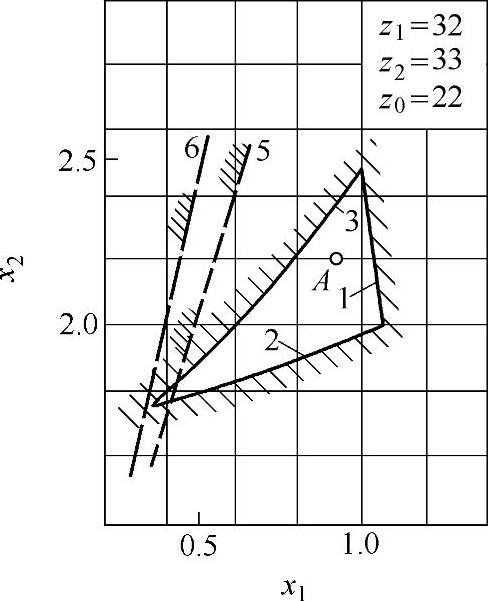
图9-18 变位系数封闭图（二）

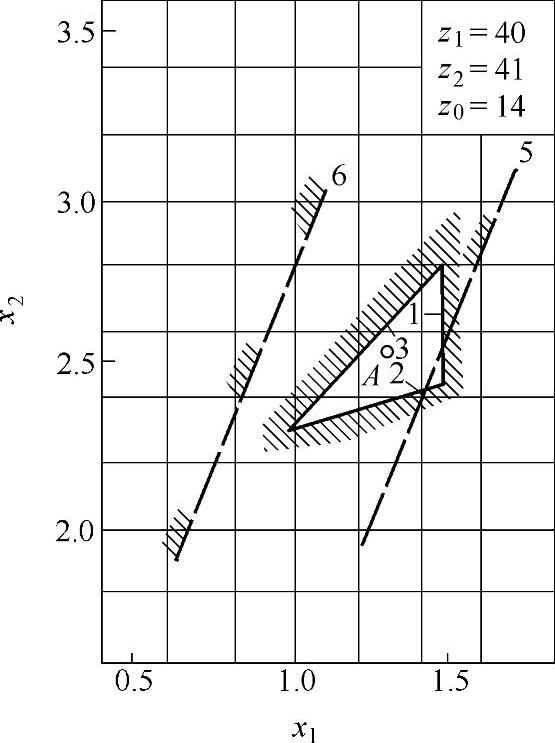
图9-19 变位系数封闭图（三）

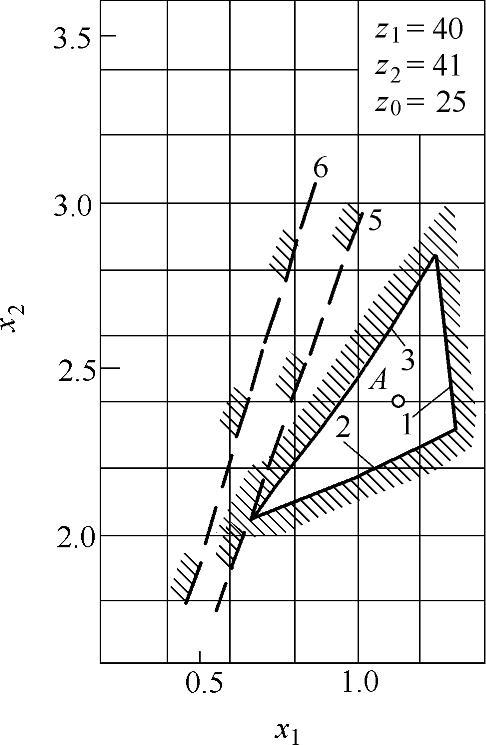
图9-20 变位系数封闭图（四）

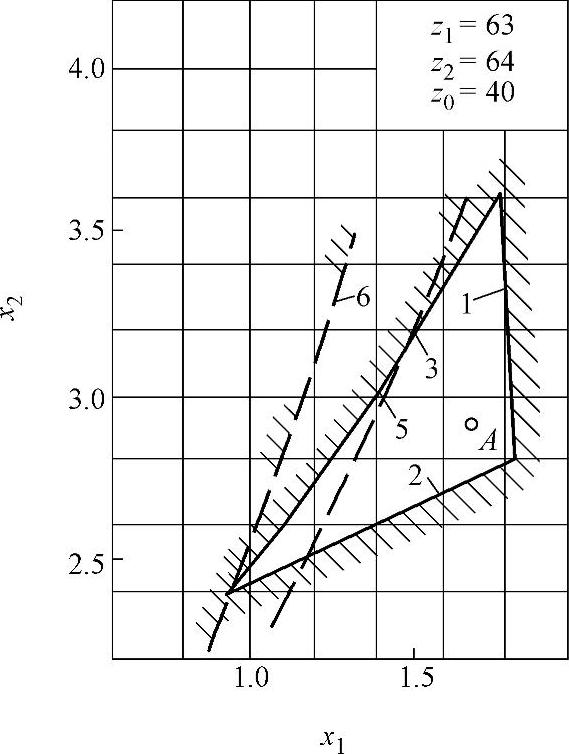
图9-21 变位系数封闭图（五）

(www.xing528.com)

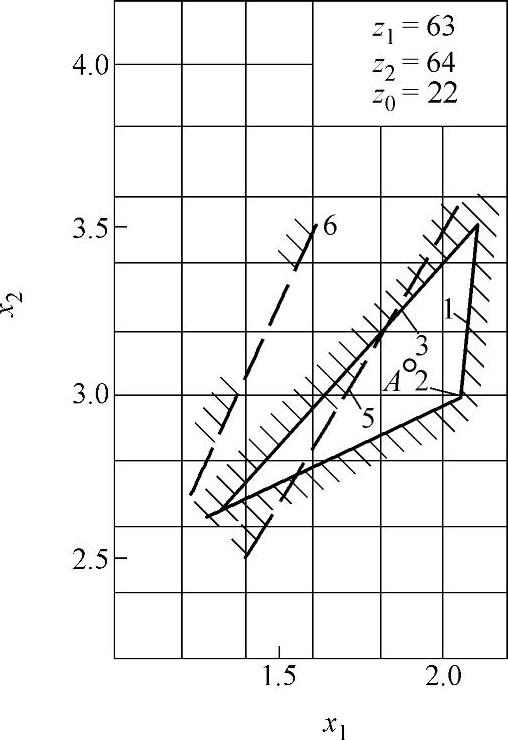
图9-22 变位系数封闭图（六）

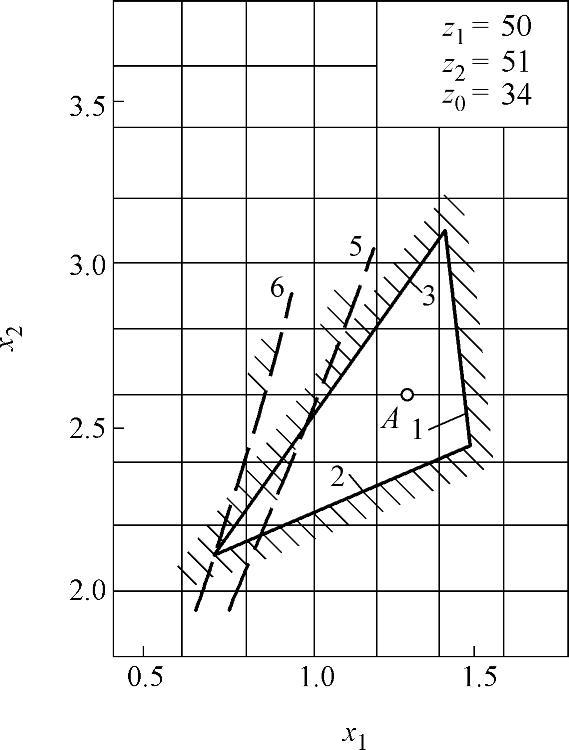
图9-23 变位系数封闭图（七）

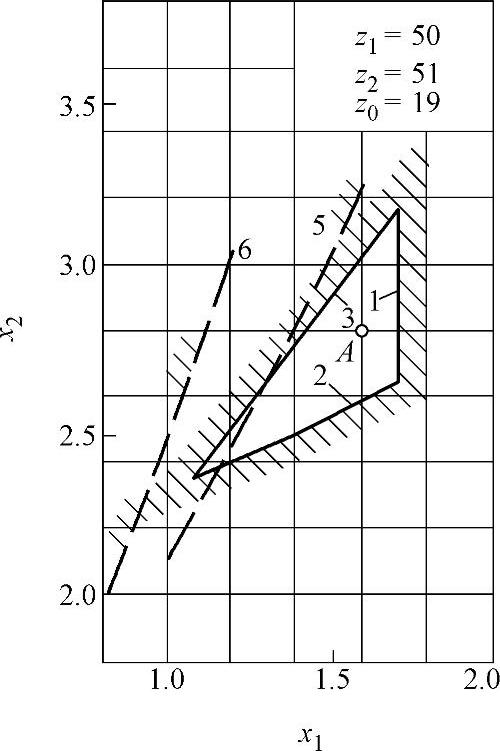
图9-24 变位系数封闭图（八）

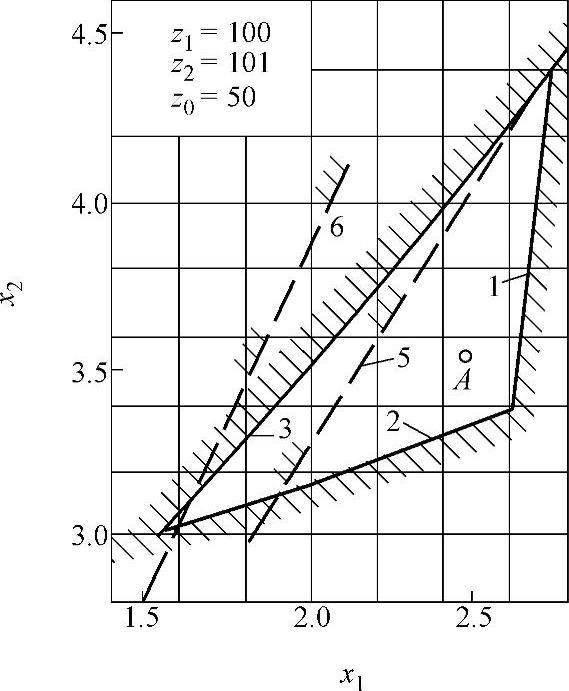
图9-25 变位系数封闭图（九）

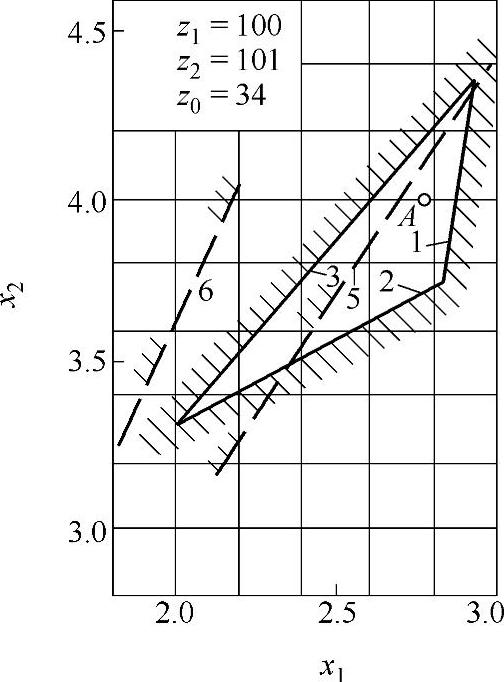
图9-26 变位系数封闭图（十）

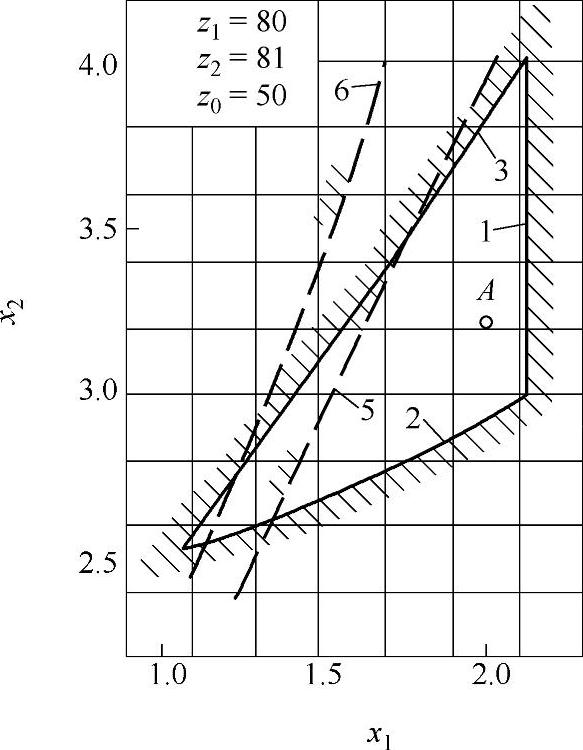
图9-27 变位系数封闭图（十一）

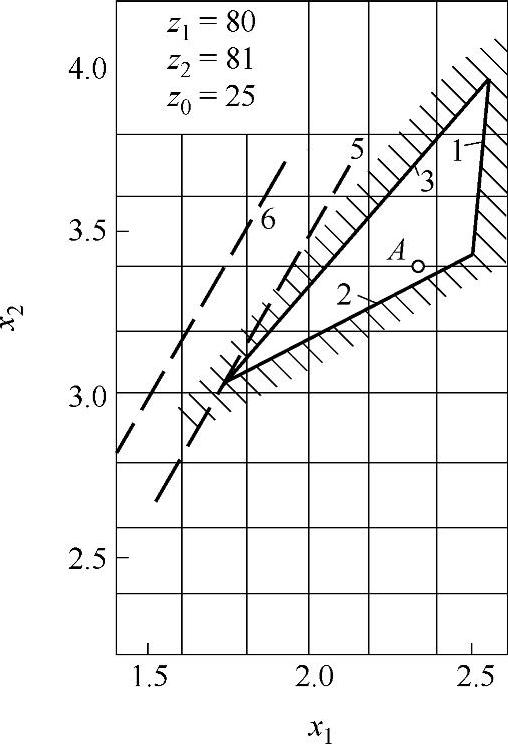
图9-28 变位系数封闭图（十二）

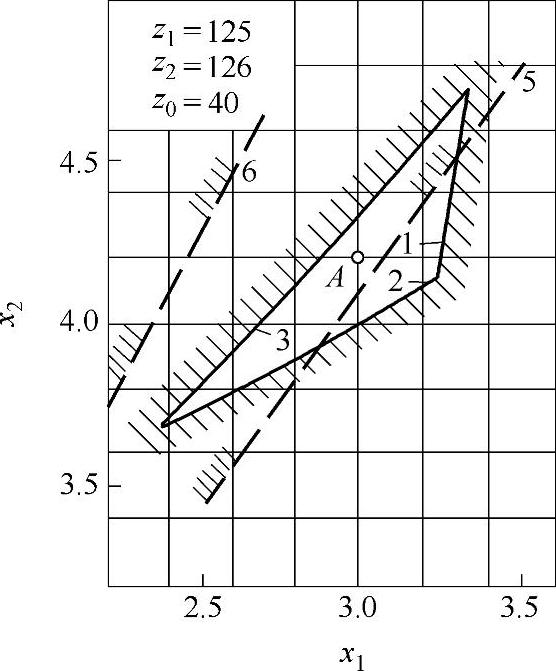
图9-29 变位系数封闭图（十三）

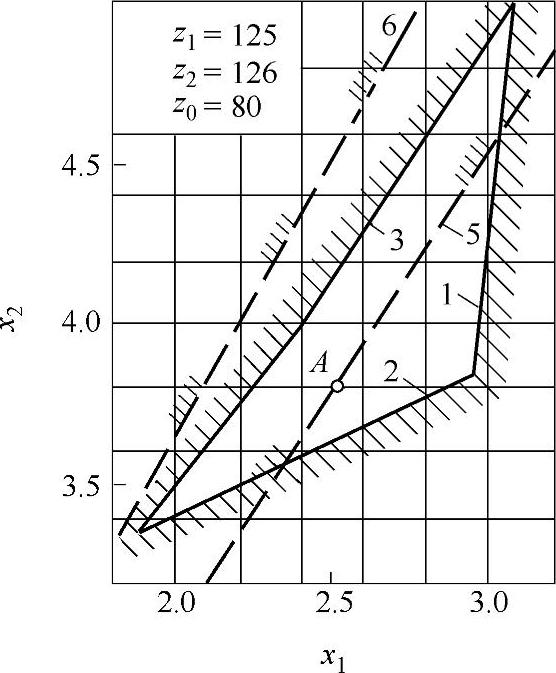
图9-30 变位系数封闭图（十四）

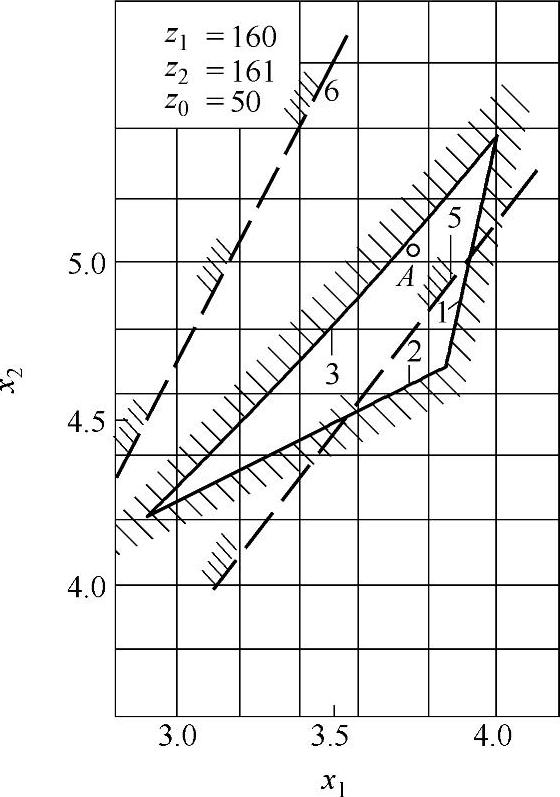
图9-31 变位系数封闭图（十五）

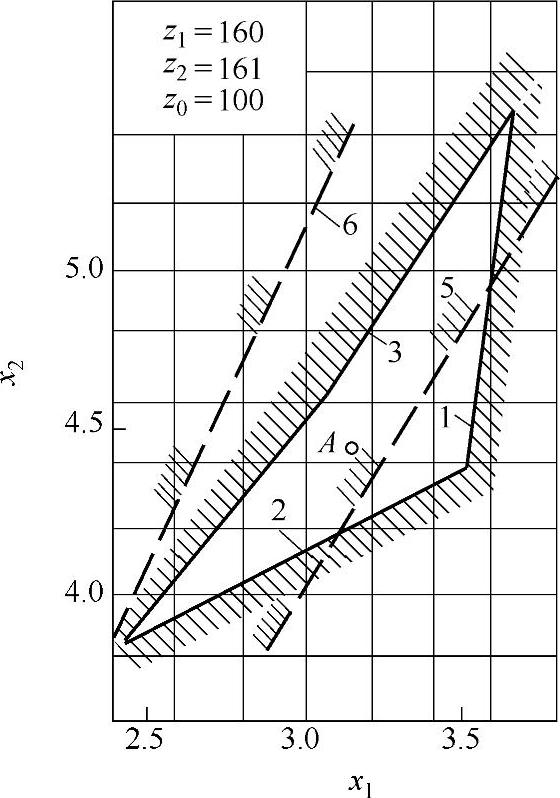
图9-32 变位系数封闭图（十六）

内齿圈齿数z₂与插齿刀齿数z₀的关系见表9-3。

表9-3 内齿圈齿数z₂与插齿刀齿数z0

封闭图是根据保持标准顶隙计算系统进行的，其中齿轮z₁的顶圆直径d_a1按下式确定

d_a1=d_f2^-2a′-2c∗m

内齿圈z₂顶圆直径d_a2计算时，不考虑齿轮z₁的加工刀具参数。为了消除在变位系数x₂较小时产生的轮齿干涉，将内齿圈z₂的齿顶缩短，于是引进系数k₂。当内齿圈z₂的变位系数x₂＜2时，k₂按下式确定

k₂=0.25-0.125x2

当x₂＞2时，则k₂=0。

于是，内齿圈的顶圆直径d_a2按下式确定

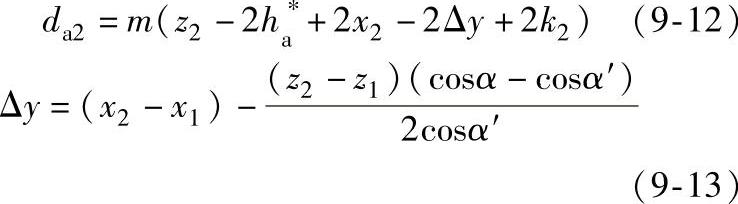
式中 Δ_y——齿顶高变动系数；

α——压力角，α=20°；

α′——啮合角。

z∑=z₂-z₁内啮合传动封闭图由下列限制曲线组成（见图9-17～图9-32）

1——重合度ε_α=1.2的限制曲线；

2——齿廓重叠干涉的限制曲线；

3——齿轮z₁齿顶厚s_a1=0.3m的限制曲线；

4——内齿圈z₂齿顶厚s_a2=0.3m的限制曲线，断续的阴影线表示选择变位系数x₁时受顶切的限制曲线；

5——加工齿轮z₁与内齿圈z₂为同一把插齿刀的限制曲线；

6——齿轮z₁用滚刀加工的限制曲线。

对于内啮合齿轮的齿数组合，没有相应的封闭图时，可用插值法来选择变位系数x₁或按如下的经验公式确定

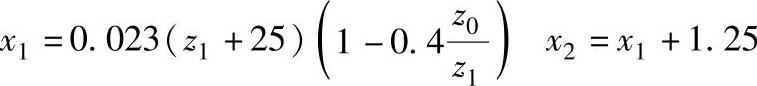
根据上式计算的x值，在大多数情况下，变位点是位于封闭图内（见图9-17～图9-32中的字母A）。但内啮合质量指标仍需校核。图9-33为一齿差内啮合齿轮副。

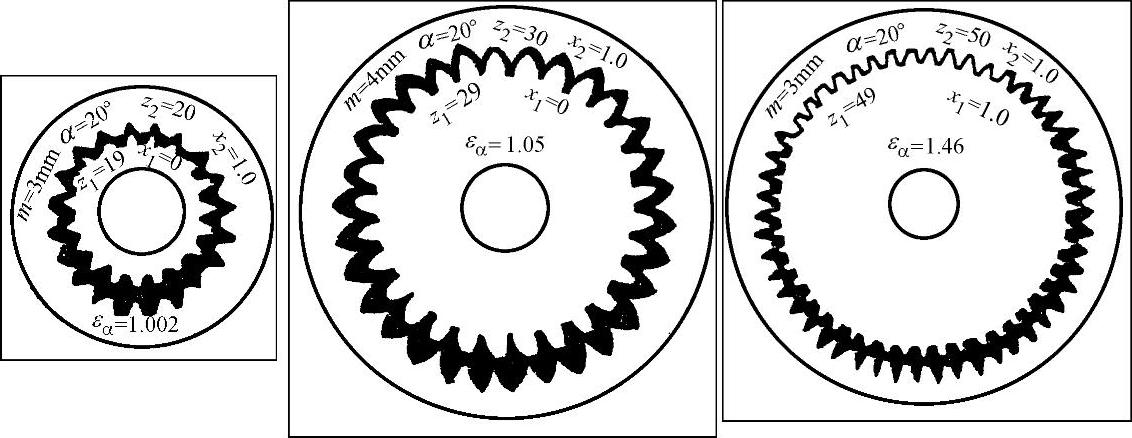
图9-33 一齿差内啮合齿轮副