齿轮弯曲疲劳强度校核计算方法优化

1.计算公式

计算齿根弯曲应力

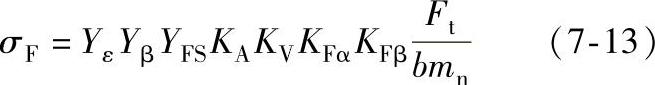
式中 m_n——齿轮的法向模数；

b——齿轮宽度，取b₁、b₂大小齿轮齿宽的小者；

F_t——作用在齿轮分度圆上的圆周力（N）。许用齿根弯曲应力

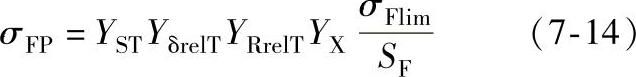
弯曲强度条件：应满足σ_F≤σ_FP。

2.系数的取值方法

1）外齿轮的齿形系数Y_FS，考虑了包括齿根圆角缺口效应在内的各种复杂应力条件。

由齿数z（或当量齿数z_V）和变位系数x由图7-23确定。

2）弯曲强度计算的重合度系数Yε

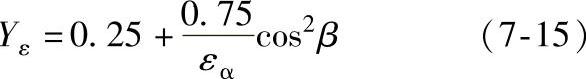
限制条件是0.625≤Y_ε≤1。

3）弯曲强度计算的螺旋角系数Yβ

限制条件是Y_β≥max[（1-0.25ε_β），（1-β/120）]。即可求出Y_ε和Y_β。

由许用齿根弯曲应力式（7-14）可知，如果小齿轮和大齿轮的弯曲疲劳极限σ_Flim不相等，则其齿根许用弯曲应力σ_FP也不相等。小齿轮和大齿轮系数Y_ST、Y_δrelT、Y_δrelT和Y_X可认为近似相等。

4）试验齿轮的应力修正系数，Y_ST=2.0。

5）相对齿根圆角敏感系数Y_δrelT可近似地取Y_δrelT=1.0；也可根据模数m_n来确定：

当m_n≤8mm时，Y_RrelT=1.00；

当8mm＜m_n≤16mm时，Y_RreT=0.9；

当m_n＞16mm时，Y_RrelT=0.96。

6）弯曲强度计算的尺寸系数Y_X；限制条件是0.8≤Y_X≤1。

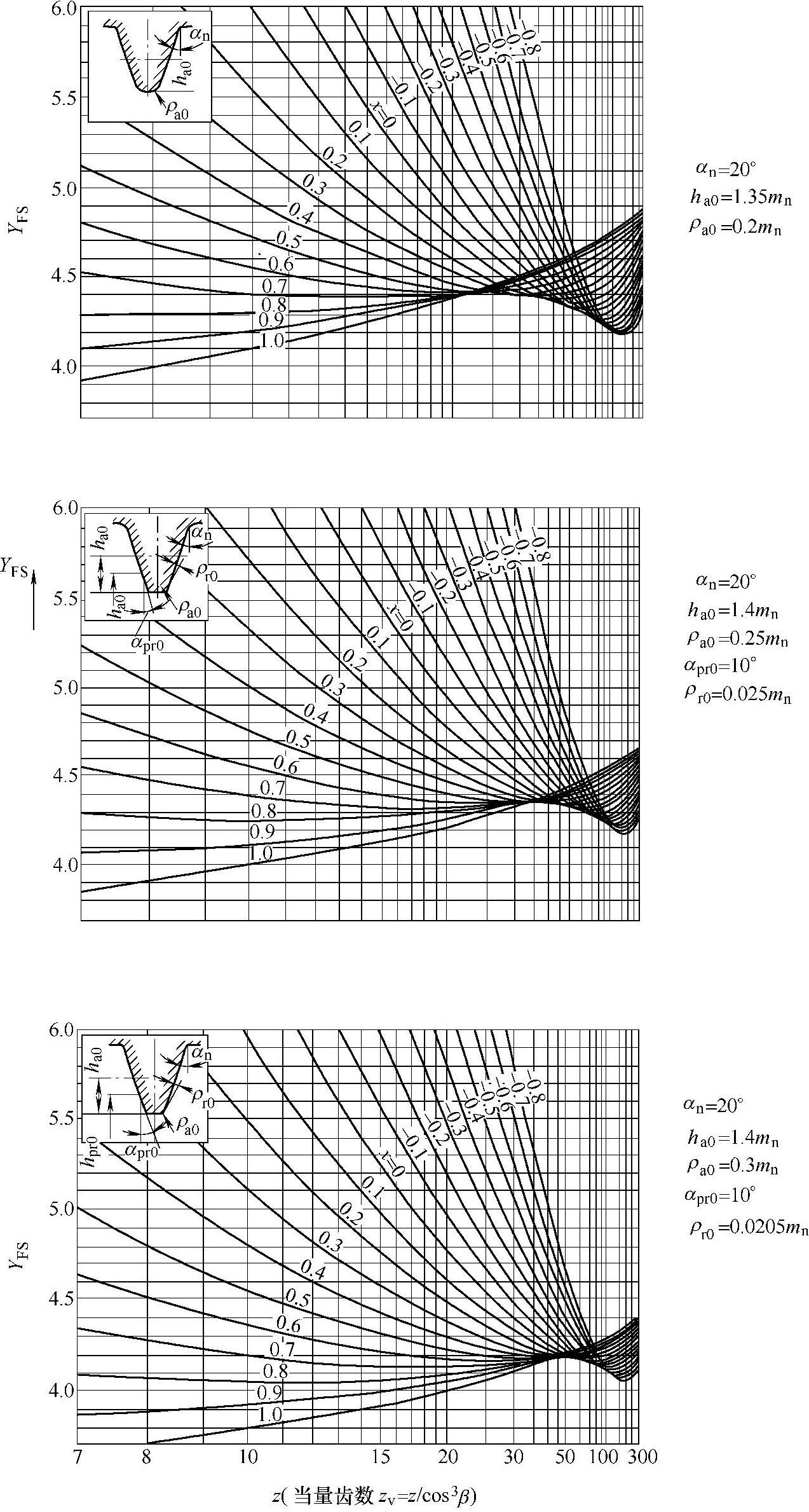
图7-23 确定YFS

7）试验齿轮的弯曲疲劳极限σ_Flim（MPa）。对于表面硬化钢制齿轮，经硬化后，齿根许用弯曲疲劳极限的范围为310～520MPa；也可由齿面硬度及材质按图7-24～图7-26确定。

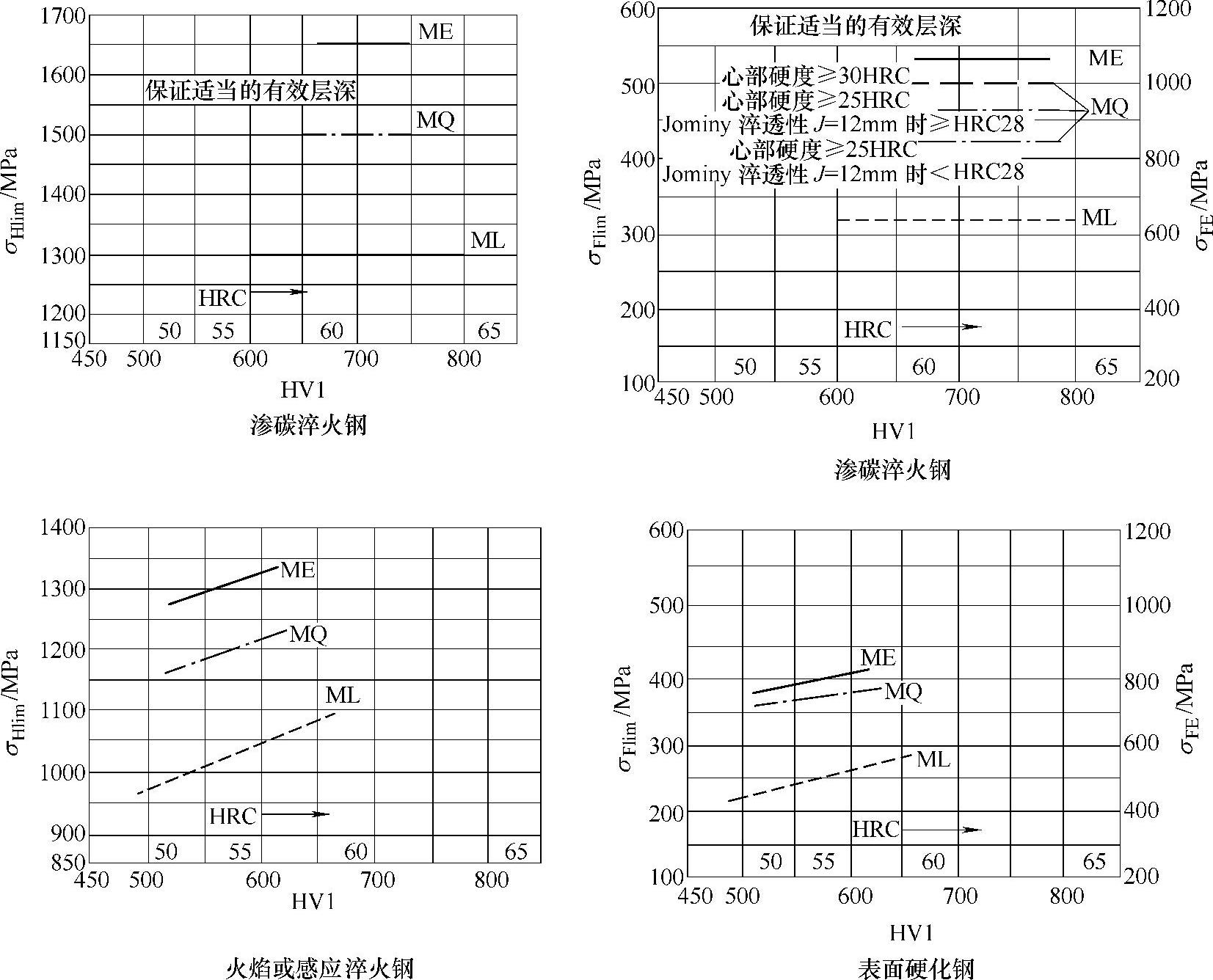
图7-24 渗碳淬火钢和表面硬化（火焰或感应淬火）钢的σ_Hlim、σ_Flim和σFE

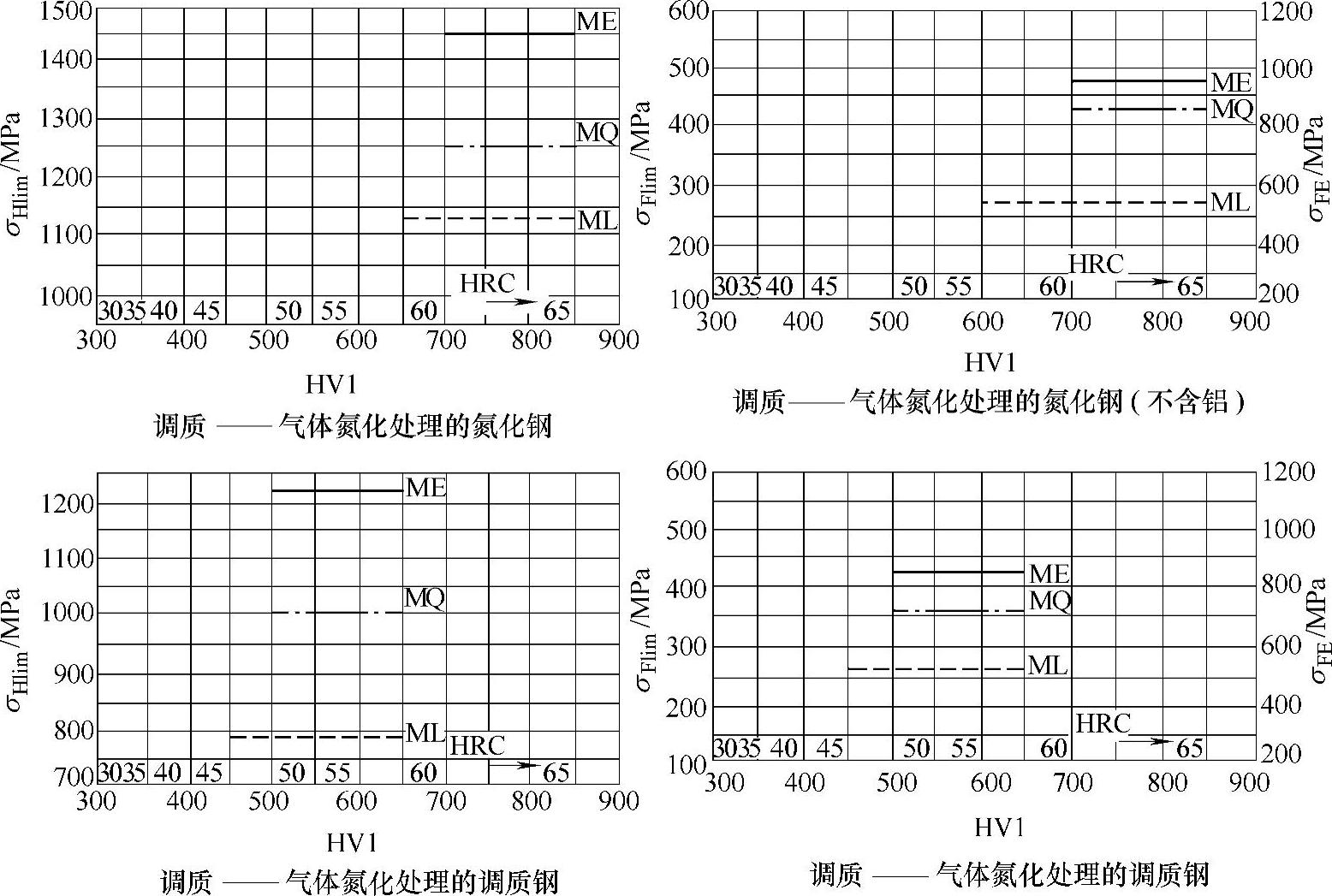
图7-25 氮化和氮碳共渗钢的σ_Hlim、σ_Flim和σFE

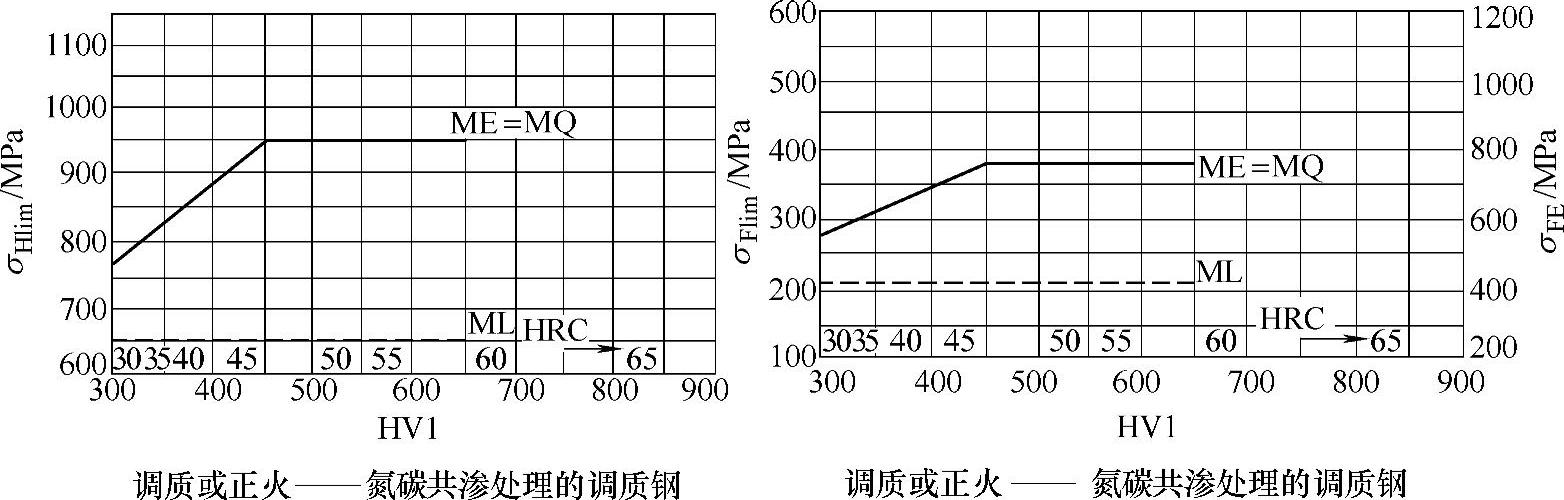
图7-25 氮化和氮碳共渗钢的σ_Hlim、σ_Flim和σ_FE（续）

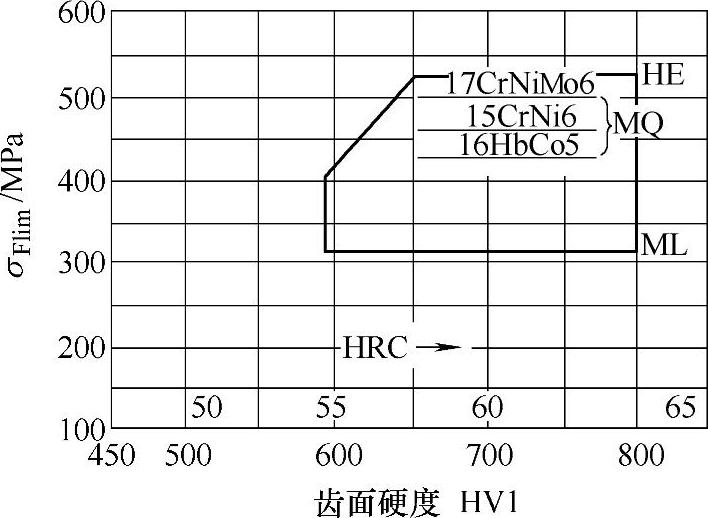
图7-26 确定σFlim

8）安全系数。根据DIN标准要求：接触强度的最小安全系数S_H=1.0；齿根弯曲强度的最小安全系数S_F=1.3。

实践中通常采用较大安全系数。在多级齿轮传动装置中，对昂贵的最后一级齿轮，采用高出10%～20%的较大安全系数，而在大多数情况下，对于廉价的初级传动齿轮采用更大的安全系数。对于有风险的应用场合，也应采用较大的安全系数。

最小安全系数的参考值见表7-6。

3.计算实例

若一电动机通过多级圆柱齿轮装置驱动一台磨煤机，现对低速级齿轮进行设计计算。

1）已知条件：额定功率P=3300kW，小齿轮转速n₁=141r/min，中心距a=815mm；法向模数m_n=22mm，齿顶圆直径d_a1=615.5mm，d_a2=1100mm，小齿轮齿宽b₁=360mm，大齿轮齿宽b₂=350mm，小齿轮齿数z₁=25，大齿轮齿数z₂=47，变位系数x₁=0.310，x₂=0.203，法向压角α_n=20°，螺旋角β=10°；润滑油运动粘度ν₄₀=320cst，平均峰顶至谷底粗糙度R_Z1=R_Z2=4.8μm；圆柱齿轮由17CrNiMo6材料制成，经表面硬化处理，齿面磨削时进行修缘修形，并具有宽度对称凸度。

2）计算（数值经过圆整）：齿数比u=z₂/z₁=47/25=1.88，小齿轮分度圆直径d₁=558.485mm，分度圆上的名义切向力F_t=800.425N，分度圆圆周速度v=4.123m/s，基圆螺旋角β_b=9.391°；当量齿数z_v1=z₁/cos³β=25/cos³10°=26.175，z_v2=z₂/cos²β=47/cos³10°=49.21，端面模数m_t=m_n/cosβ=22/cos10°mm=22.339mm，端面压力角α_t=20.284°，端面啮合角α′_t=22.244°，端面法向基圆齿距p_bt=65.829，基圆直径d_b1=523.852mm，d_b2=984.842mm，接触线长度g_ε=98.041mm，端面重合度ε_α=1.489，纵向重合度ε_β=0.879。

使用系数K_A=1.50（平稳运转模式的电动机，中等冲击负荷的磨煤机），动载系数K_V=1.027，接触强度计算的齿向载荷分布系数K_Hβ=1.20，[根据式（7-5），取K_Hβ=1.326，然而由于齿形对称凸度，可以较小值进行计算]，弯曲强度计算的齿向载荷分布系数K_Fβ=1.178，接触强度和弯曲强度计算的齿间载荷分配系数K_Hα=K_Fα=1.0。

①计算齿面接触强度的承载能力。弹性系数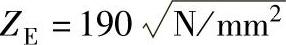，节点区域系数Z_H=2.342，螺旋角系数Z_β=0.992，重合度系数Z_ε=0.832。小齿轮和大齿轮的接触应力σ_H=1251MPa。润滑剂系数Z_L=1.047，速度系数Z_V=0.978，表面粗糙度系数Z_R=1.018，工作硬化系数Z_W=1.0，尺寸系数Z_X=0.94，给出试验齿轮接触疲劳极限σ_Hlim=1500MPa。

首先由式（7-9），在不考虑安全系数的条件下，求出齿面许用接触应力σ_HP=1470MPa。

由S_H=σ_HP/σ_H=1470/1251=1.18，求出接触强度安全系数。与转矩有关的安全系数是。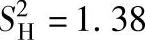

②计算齿根弯曲强度的承载能力。重合度系数Y_ε=0.738，螺旋角系数Y_β=0.927，齿形系数Y_FS1=4.28，Y_FS2=4.18（对于h_a0=1.4m_n，ρ_a0=0.3m_n，α_pro=10°，p_ro=0.0205m_n）。

由式（7-13）求出小齿轮齿根弯曲应力σ_F1=537MPa，大齿轮齿根弯曲应力σ_F2=540MPa。

试验齿轮的应力修正系数Y_ST=2.0，相对齿根圆角敏感系数Y_δrelT=1.0，相对齿根表面状况系数Y_RrelT=0.96，尺寸系数Y_X=0.83。不考虑安全系数，取齿根弯曲疲劳极限σ_Flim=500MPa。(www.xing528.com)

可由式（7-14）求得小齿轮和大齿轮的齿根许用弯曲应力σ_FP1=σ_FP2=797MPa。

与转矩有关的齿根抗弯强度的安全系数S_F=σ_F/σ_FP，对小齿轮S_F1=797/537=1.48，对大齿轮S_F2=σF2/σFP2=797/540=1.48。

4.齿轮装置类型

（1）标准设计 工业实践中使用不同类型的齿轮装置，但常使用的是具有固定传动比和尺寸等级的标准斜齿圆柱齿轮和弧齿锥齿轮装置。这些根据模块式结构体系制造的单级至4级齿轮装置，可满足从动机范围广泛的速度和转矩要求。与标准电动机配合使用，这种齿轮装置通常是最经济的传动设备。

但还有一些不使用标准驱动设备的情况。在此类情况中，要数转矩超过标准齿轮装置范围的情况最为典型。在此情况下，采用特殊设计的齿轮装置，其中载荷分配齿轮装置起的作用最为重要。

（2）载荷分配齿轮装置 原则上，齿轮装置的最大输出转矩受制造设施的限制，因为齿轮加工机床切削的最大齿轮直径是有限的。因此，输出转矩的进一步增大，只有通过齿轮装置中的载荷分配才能实现。然而，载荷分配齿轮装置也广泛用于小转矩场合，因为载荷分配齿轮装置具有某些优点，尽管内部组件数量较多。其中有些载荷分配齿轮还可采用标准设计。下面将给出这类齿轮装置的一些典型特性。

（3）各种齿轮装置的比较 下面讨论传动比最高达i=8的单级和两级传动齿轮装置。在普通齿轮装置中，最后一级、或最后两级齿轮的重量占总重量的大约70%～80%，而且制造费用也占总制造成本的70%～80%，为获得更高的传动比而增加齿轮传动级，并不会给下述基本事实带来什么大变化。图7-27所示为没有载荷分配和有载荷分配的齿轮装置，轴1均为高速轴，轴2均为低速轴。当已知转速n₁、n₂时，可得传动比i=n₁/n₂。

图7-27所示齿轮的直径比相当于传动比i=7。图中所示齿轮装置具有相同的输出转矩。图7-27是按比例绘制的，以便于尺寸对比。图中，a～c三种齿轮装置为偏置轴布置，d～g四种则为同轴布置。

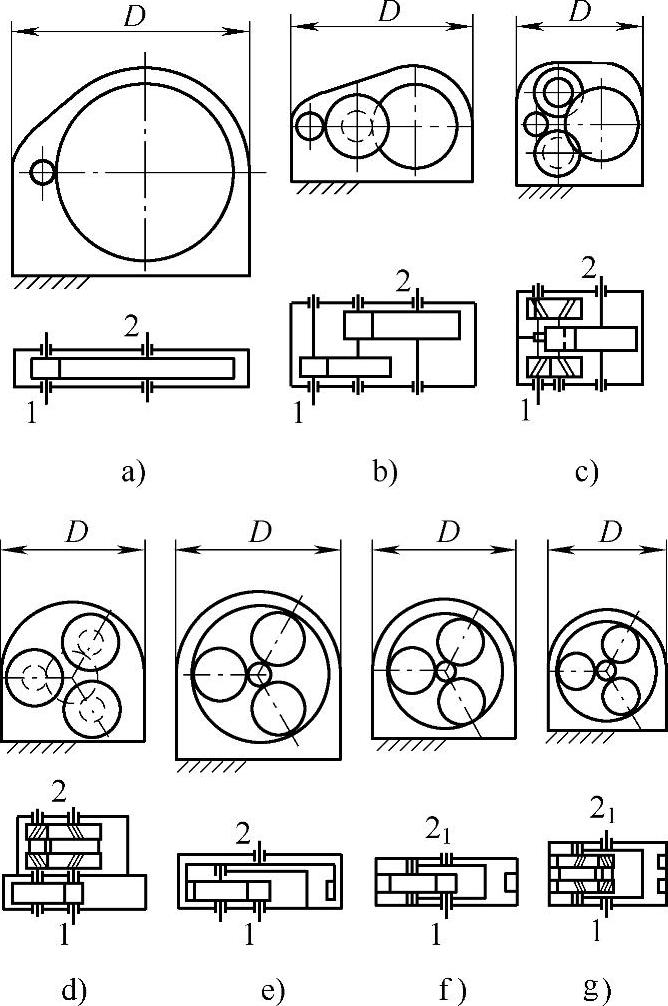
图7-27 没有载荷分配和有载荷分配的齿轮装置的图示

图7-27中，齿轮装置a为一级传动，b为两级传动，两种齿轮装置均为无载荷分配；齿轮装置c～g均为两级传动，而且均为载荷分配齿轮装置。齿轮装置c和d中的空转齿轮具有不同的直径。在齿轮装置e～g中，一根轴上的空转齿轮已并入驱动齿轮，所以它们也被视为单级齿轮装置。

齿轮装置c为双载荷分配齿轮，通过双斜齿和轴1的轴向可移动性，从而在高速级获得均匀的载荷分配。

在齿轮装置d中，高速级的载荷相等地在三个中间齿轮之间分配，这种均匀分配是通过轴1上的中心齿轮的径向可移动性实现的。在低速级，载荷通过双斜齿和中间轴的轴向可移动性可由各齿轮共同分担，总承载能力可提高6倍。

在齿轮装置e～g中，为了获得三个中间齿轮间的载荷相等分配。轴1上的中心齿轮绝大多数情况下是可以径向移动的。大的内齿轮是一个中空的内齿圈。在齿轮装置e中，此齿圈与轴2连接；而在齿轮装置f和g中，则与齿轮箱体连接。在齿轮装置f和g中，齿轮幅板和轴2形成一个整体。空转齿轮作为行星齿轮围绕中心齿轮转动。在齿轮装置g中，双斜齿和空转齿轮的轴向可移动性，保证了6个分支之间的载荷分布均匀。

1）载荷值。通过载荷值B_L，就能在下面的研究中，对具有不同齿轮材料极限应力值的圆柱齿轮传动装置进行相互比较。

载荷值是与小齿轮节圆直径d′₁和承载齿宽b有关的轮齿圆周力F_t为

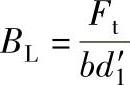
采用近似方法，根据接触强度可用下式求得圆柱齿轮的啮合许用载荷值为

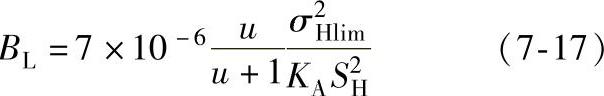
式中 B_L——圆柱齿轮的啮合许用载荷值（MPa）；

σ_Hlim——许用接触应力（MPa）；

K_A——使用系数；

u——齿数比，u=z₂/z₁＞1对于内齿轮为负值。

载荷值B_L与圆柱齿轮装置的尺寸无关。下列参数值适用于实际使用的齿轮装置。对表面硬化钢制的圆柱齿轮，B_L=4～6MPa；对调质钢圆柱齿轮，B_L=1～1.5MPa。对于钢制内齿圈调质、太阳轮和行星轮钢制表面硬化的行星齿轮传动B_L=2.0～3.5MPa。

2）参考转矩。图7-28所示为根据传动比i对各种类型圆柱齿轮装置进行比较。当比较尺寸时，转矩T₂以结构尺寸D为参照；当比较质量时，以齿轮装置质量G为参照；当比较轮齿表面积时，以生成的节圆柱表面积A为参照。齿轮装置的质量G和轮齿表面A（即生成的表面）是衡量制造成本的一个尺度。图7-28所示的曲线越高，相应的齿轮就比其他齿轮更好。

对于图7-28中说明的所有齿轮装置，均满足以下相同的先决条件。对所有齿轮装置，尺寸D比节圆直径之和大1.15倍。齿高和齿宽具有相同的定义。此外，齿轮箱厚度与结构尺寸D保持固定关系。

已知转矩T₂和根据式（7-17）计算出载荷B_L，利用图7-28给定传动比i，就能近似求出结构尺寸D、齿轮装置质量G，以及轮齿表面积A。然而，模块式齿轮装置的质量通常都比这样求得的大，因为齿轮箱尺寸是根据不同观点确定的。

在小传动比i条件下，就其尺寸和质量而言，行星齿轮装置f和h具有最大转矩。当传动比i＜4时，行星轮变成了小齿轮而不是中心齿轮。行星轮需要的空间及轴承承载能力均大为减小。通常情况下，对于传动比i＜4.5的齿轮装置，行星轮轴承布置在行星架中。当传动比i=7时，就其尺寸和质量而言，只有外齿轮结构形式的齿轮装置c和d具有最大的转矩。行星齿轮传动与其他齿轮装置比较，仅在小传动比的情况下，以轮齿表面为参照的转矩才更有利。然而，要考虑到，在制造质量相同的情况下，内齿轮的制造费用高于外齿轮的制造费用。

比较表明，还没有在整个传动比范围内能综合所有优点的最佳齿轮装置。因此，以尺寸和质量为参照的输出转矩，对行星传动最有利，而且行星传动的传动越小，就越是如此。然而，随着传动比的增加，参考转矩大为减小。当传动比i=8时，只对具有外齿轮的载荷分配齿轮装置更有利，因为随着传动比的增加，参考转矩只略微减小。

在轮齿表面积方面，如果只与具有外齿轮的载荷分配齿轮装置比较，行星齿轮传动就没有那么大的优越性了。

3）效率。当比较效率时，在图7-28d中，只考虑了啮合中的功率损失。满负荷条件下，啮合中的功率损失大约占滚子轴承、普通圆柱齿轮装置总功率损失的85%。当输入功率在轴1上，可由下面的关系式求出以转矩表示的效率。

图7-28所示的全部齿轮装置均有相同的齿形摩擦系数μ=0.06。另外，对所有齿轮装置都假定齿轮没有采用高变位，以及小齿轮齿数均为z=17，这样就能进行比较。

单级传动齿轮装置a具有最佳效率。两级齿轮装置b～h的效率较低，因为功率传递要通过两次啮合。与齿轮装置b、c、d比较（这三种齿轮装置均带有外齿轮），齿轮装置e、f、h在啮合过程中的滑动速度较低，所以这三种齿轮装置中的内齿轮副效率较高。

行星齿轮传动f和h的无损失耦合性能使其效率得到进一步提高。因此其效率比其他可比的载荷分配齿轮装置高。然而，为了达到更高的传动比，就要串联布置更多的行星齿轮传动级，结果就会冲减与齿轮装置b、c、d相比效率更高的优点。

4）举例。已知：两个f型行星齿轮减速级串联布置，总传动比i=20，输出转矩T=3×10⁶N·m，载荷B_L=2.3N/mm²。通过高速齿轮级和低速齿轮级的i=5、4的传动比分量，可近似地获得最小质量。根据图7-28b，在γ=30m·mm²/kg和γ=45m·mm²/kg时，高速齿轮级的质量大约是10.9t，低速齿轮级的质量大约为30t，即总重40.9t。根据图7-28d得出的总效率η=0.986×0.985=0.971。

然而，与具有相同传动比i=20和相同输出转矩T₂=3×10⁶N·m的d型齿轮装置相比，根据图7-28，比f型行星齿轮传动装置具有更好的载荷值，B_L=4N/mm²，其质量为68.2t，γ=11m·mm²/kg，比d型齿轮装置重67%。其优点是效率更高，即η=0.98。f型齿轮装置的两个行星齿轮传动级合起来的功率损失，比d型齿轮装置的功率损失高45%。另外，当i=4时，齿轮级中没有足够的空间安装行星轮的滚子轴承。

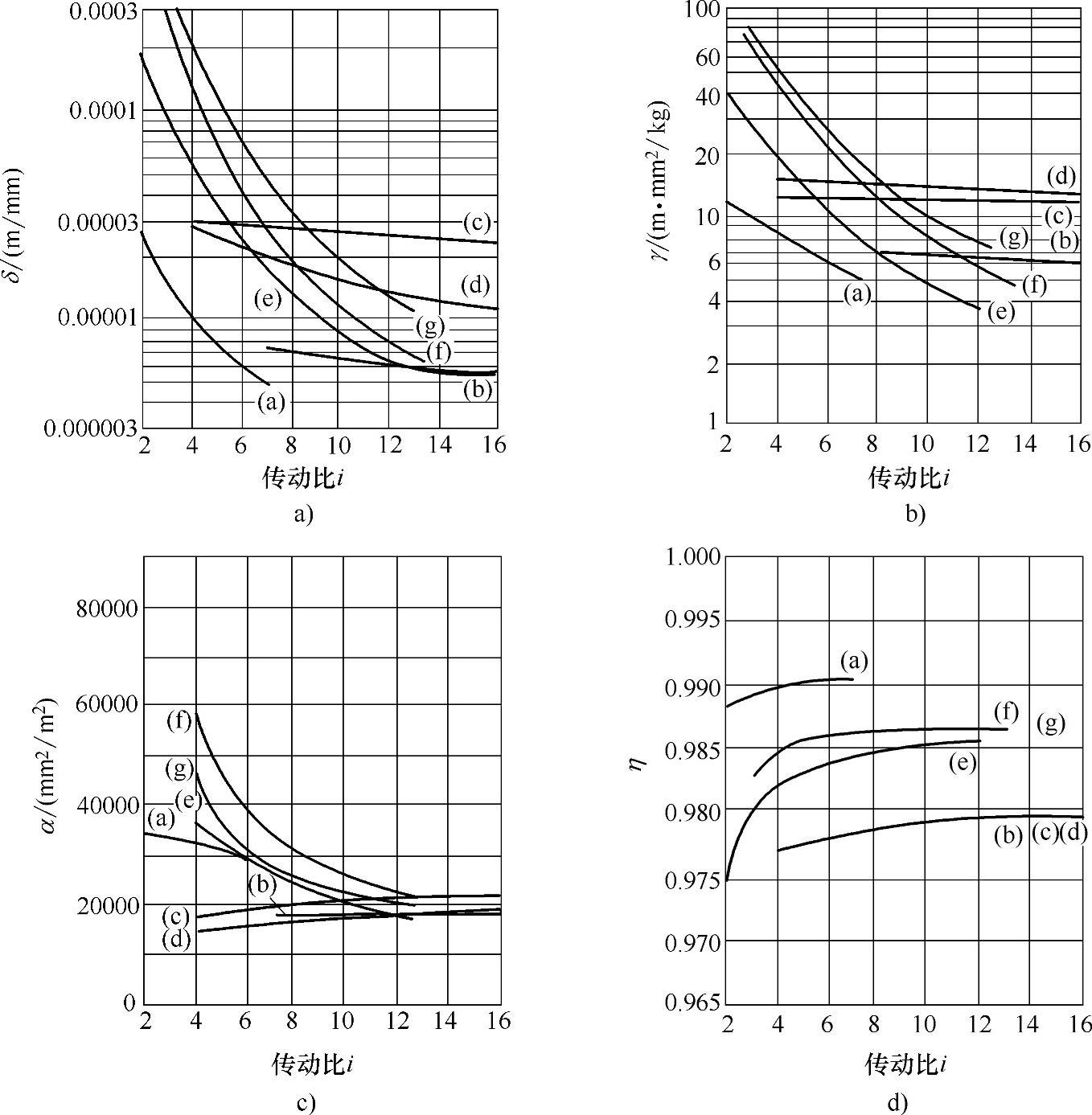
图7-28 根据传动比i对各种类型圆柱齿轮装置进行比较

a）以尺寸为参照的转矩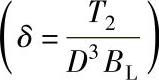

b）以齿轮装置质量为参照的转矩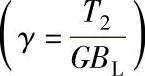

c）以齿面为参照的转矩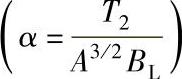

d）满负荷效率

5.轮齿静强度核算

当齿轮工作中可能出现短时间、少次数（N_L≤N₀）超过额定工况的大载荷时，应进行静强度核算。N_L＞N₀的载荷应纳入疲劳强度计算。静强度的基本核算公式见表7-7。

表7-7 轮齿静强度核算公式

注：各式中F_tmax为按载荷谱中实测或预期的最大载荷T_max（如启动转矩、堵转转矩、短路或其他过载转矩）计算的圆周力（N）；其余代号的意义和取值同疲劳强度计算。