(1)负号机构 在负号构构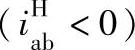 中,轮a、轮b和轮H有三个外伸轴,其中轮b为固定轮,应用式(6-152),则得
中,轮a、轮b和轮H有三个外伸轴,其中轮b为固定轮,应用式(6-152),则得
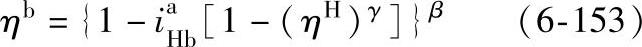
式中
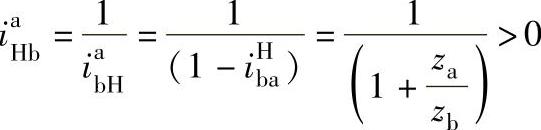
当轮a主动时,β=+1,γ=+1;当轮a从动时,β=-1,γ=-1。代入上述β、γ值,式(6-153)可改写成
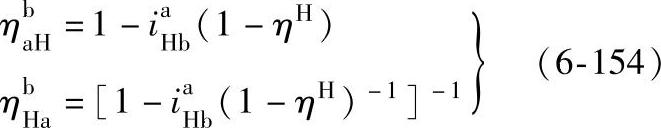
通过整理,上面第二式也可变成
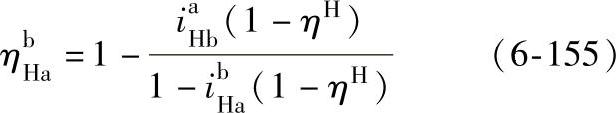
对于负号机构,由上述可知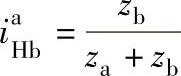 ,
,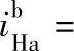
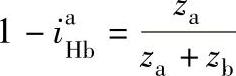 ,都是介于0与1之间的小数,而(1-ηH)是一个更小的小数,故
,都是介于0与1之间的小数,而(1-ηH)是一个更小的小数,故
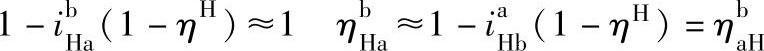
此外,由此式也可看出ηb>ηH。
总之,2K-H型负号机构,不管轮a主动还是轮H主动,可以用统一的简化公式
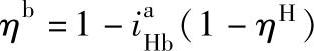
计算行星齿轮传动的效率。此外,这种行星轮系的效率大于其转化机构的效率ηH。
据国内、外专家测定,单级行星传动效率为η=0.96~0.98;两级行星传动效率为η=0.94~0.96;三级行星传动效率为η=0.92~0.94;四级行星传动效率为η=0.89左右。
(2)正号机构 对于正号机构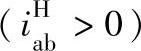 ,如2K-H(NN)型行星传动,其效率为
,如2K-H(NN)型行星传动,其效率为
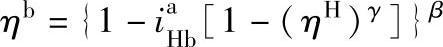
式中
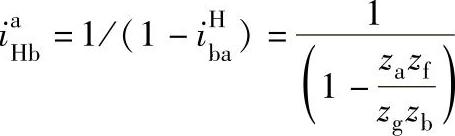
当zb>za时,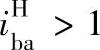 ,
,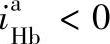 ;当zb<za时,
;当zb<za时,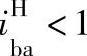 ,
,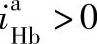 。所以β、γ的正、负有四种组合的可能。一般情况下,
。所以β、γ的正、负有四种组合的可能。一般情况下,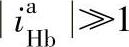 ,故计算ηb的四个式子不能合并,否则误差太大。另外,
,故计算ηb的四个式子不能合并,否则误差太大。另外,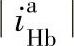 越大,ηb越低,而且ηb<ηH,特别在增速时有可能ηb<0而产生自锁现象。
越大,ηb越低,而且ηb<ηH,特别在增速时有可能ηb<0而产生自锁现象。
于是可得出如下结论:2K-H型正号机构的效率计算,应首先计算β、γ的正、负,一般正号机构的效率低于转化机构的效率,增速时有可能产生自锁。
(3)主动件与轮系效率的关系 下面研究一下太阳轮a主动和行星架H主动时,哪一种情况效率高。
1)负号机构。如上所述,因为
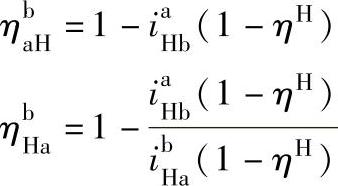
而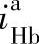 和
和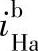 都是小于1的正数,由此可见
都是小于1的正数,由此可见

2)正号机构。根据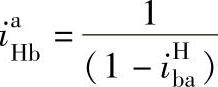 有两种情况:
有两种情况:
①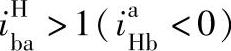 时
时
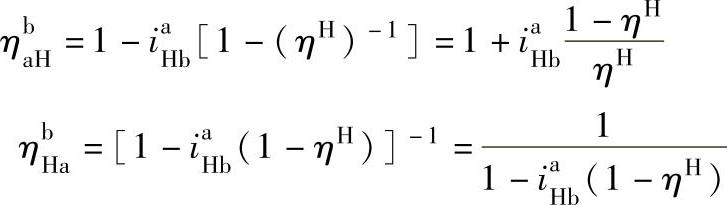
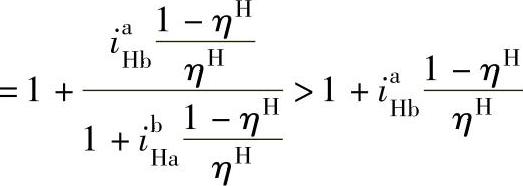
又因为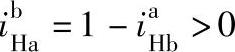 ,即
,即

②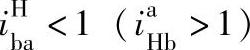 时
时
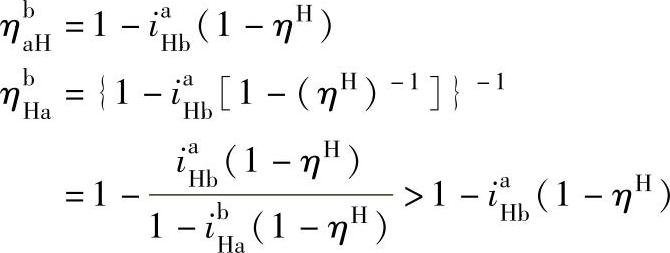
又因为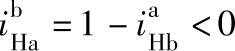 ,得
,得

综合式(6-156)、式(6-157)和式(6-158)可得出如下结论:2K-H型负号机构中轮a主动时效率高,正号机构时,则行星架H主动时效率高。
通常在设计时,各类单级2K-H型行星齿轮传动的效率按表6-35所列的公式进行计算,2K-H型行星差动传动(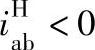 )的效率计算公式列于表6-36,两级2K-H型行星齿轮传动的效率计算公式列于表6-37。(https://www.xing528.com)
)的效率计算公式列于表6-36,两级2K-H型行星齿轮传动的效率计算公式列于表6-37。(https://www.xing528.com)
表6-35 2K-H型行星齿轮传动的效率计算公式
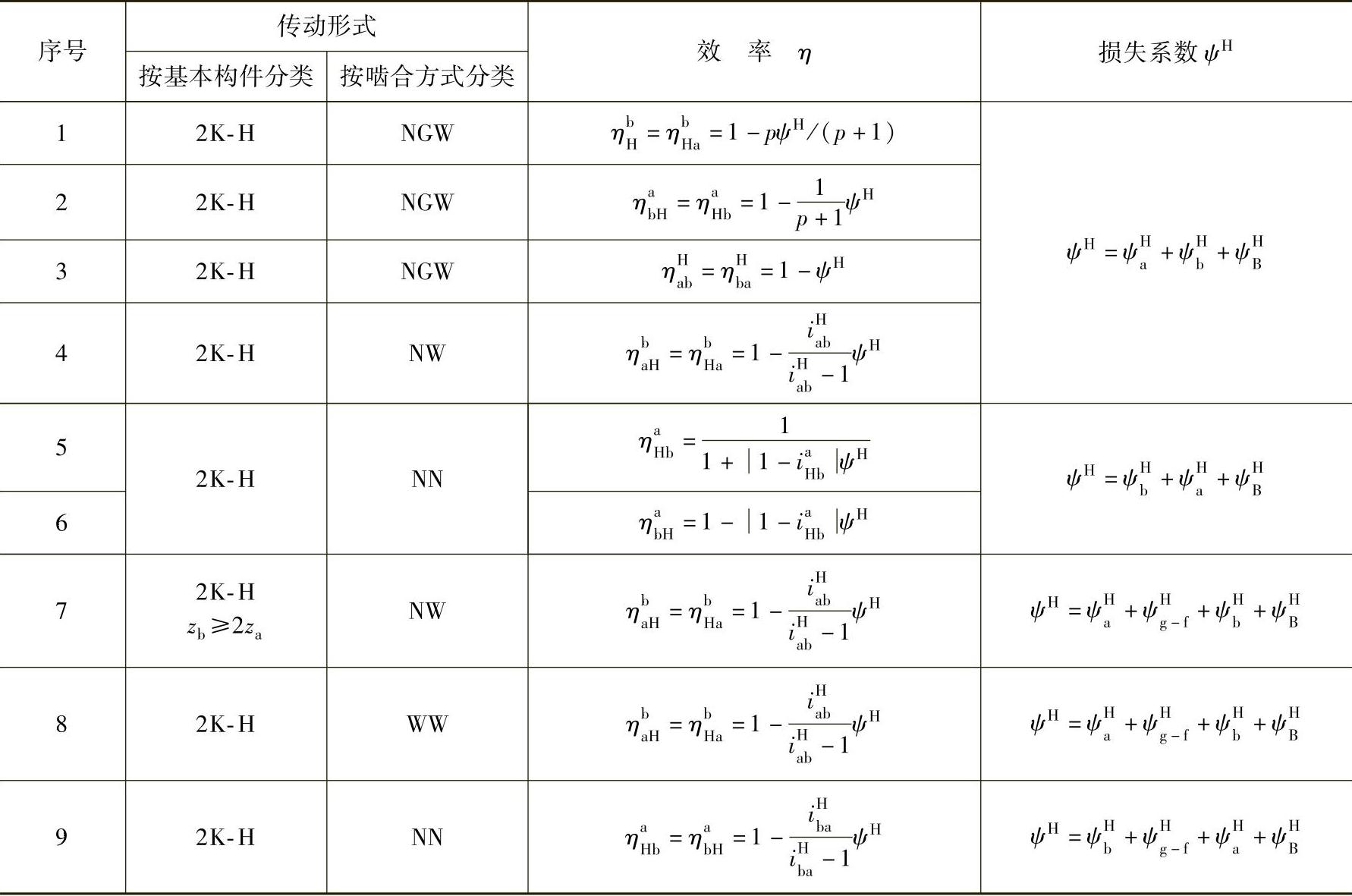
注: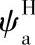 为a-g副啮合的损失系数,ψb为g-b副的啮合损失系数,
为a-g副啮合的损失系数,ψb为g-b副的啮合损失系数,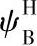 为轴承的损失系数,ψH为总的损失系数,一般取ψH=0.025。当行星轮个数np≥3时,
为轴承的损失系数,ψH为总的损失系数,一般取ψH=0.025。当行星轮个数np≥3时,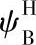 值仅考虑行星轮的轴承损失,并推荐取
值仅考虑行星轮的轴承损失,并推荐取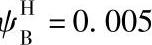 ;当np=1时,必须考虑行星轮轴承和基本构件中轴承的损失,这时推荐取
;当np=1时,必须考虑行星轮轴承和基本构件中轴承的损失,这时推荐取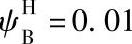 ,式中p=zb/z。
,式中p=zb/z。
表6-36 2K-H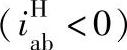 行星差动传动的效率计算公式
行星差动传动的效率计算公式

注:表中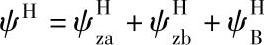 。
。
表6-37 两级2K-H型行星齿轮传动的效率计算公式
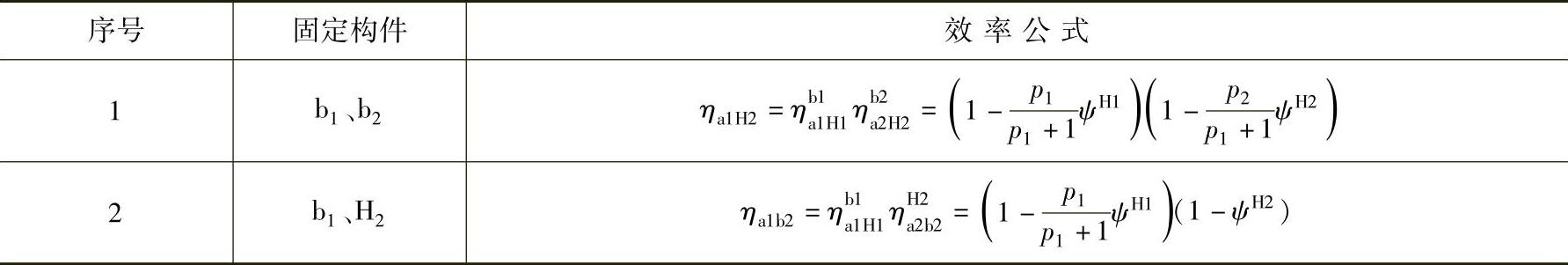
注:式中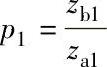 ;
;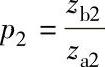 ;
;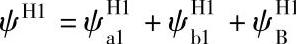 ;
;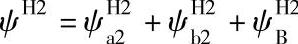 。
。
现用实例说明上述的应用。
例6-13 图6-85所示为浇铸用起重机的行星差动减速器的运动简图。太阳轮a由电动机M2驱动,内齿圈b是可动的,其外面上具有外啮合圈2,由电动机M1通过齿轮1来带动。因此,这个行星差动减速器系由一个2K-H型行星轮系和一对定轴轮系(齿轮1、2)组成。知za=23、zg=36、zb=95、z1=28、z2=115,电动机M1、M2的转速均为735r/min。试按不同工况确定输出(即行星架H)的转速nH,并计算传动效率。
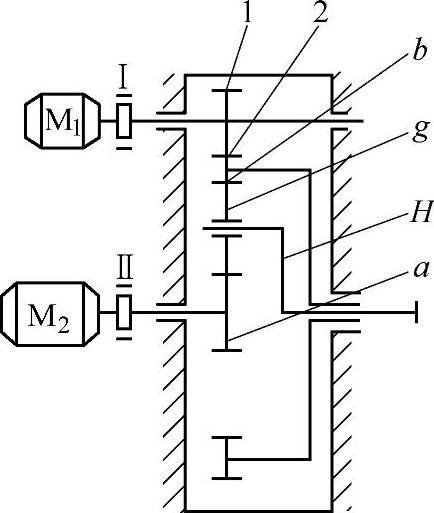
图6-85 行星差动减速器
解 1)按传动比、邻接、同心、装配条件校核均满足要求。
2)计算转速nH
①当制动器Ⅰ制动时,即nb=0,则行星传动的传动比为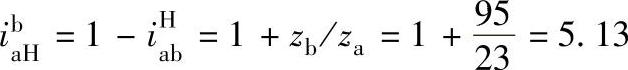 ,输出轴转速
,输出轴转速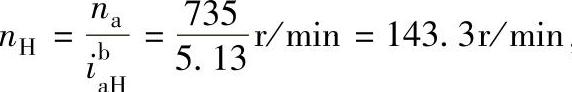 ,nH与na的转向相同。
,nH与na的转向相同。
②当制动器Ⅱ制动时,即na=0,则行星传动的传动比为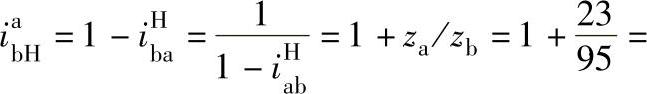
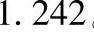 。定轴轮系的传动比
。定轴轮系的传动比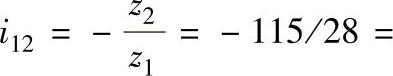
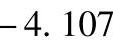 ,两轮系的总传动比
,两轮系的总传动比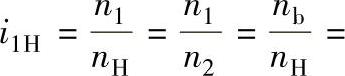
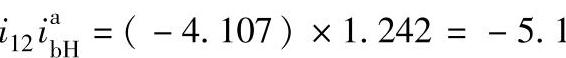 。这时输出轴的转速为
。这时输出轴的转速为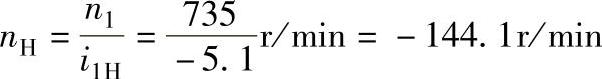 ,nH与n1的转向相反。由于上述两种工况的输出转速很接近,因此,即使其中有一电动机发生故障时,起重机通过变换电动机的转向还能照常工作。该行星差动减速器的结构如图6-86所示。
,nH与n1的转向相反。由于上述两种工况的输出转速很接近,因此,即使其中有一电动机发生故障时,起重机通过变换电动机的转向还能照常工作。该行星差动减速器的结构如图6-86所示。
③当电动机M1和M2反向转动时,即na=-735r/min,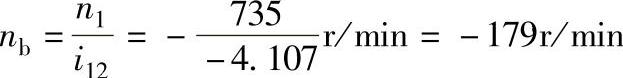 ,代入差动轮系公式得
,代入差动轮系公式得
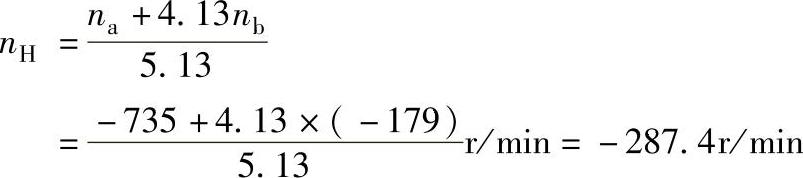
nH与na的转向相同。
④当电动机M1和M2同向转动时,即na=-735r/min,nb=179r/min,代入差动轮系公式得
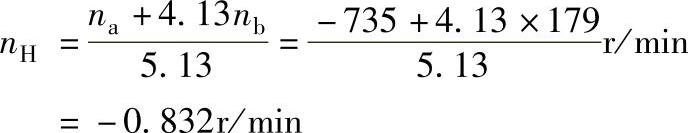
nH与na的转向相反。
⑤行星齿轮传动(a、b、H)的效率计算。减速器全部采用滚动轴承,为了节省篇幅,这里对轴承损失系数和油阻系数未单独进行计算,只是取摩擦因数为0.1,并考虑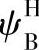 、
、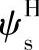 系数的影响。于是,传动损失系数
系数的影响。于是,传动损失系数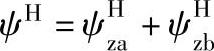 。
。
a-g副啮合的损失系数
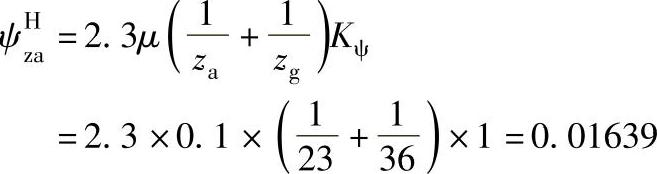
g-b副啮合损失系数
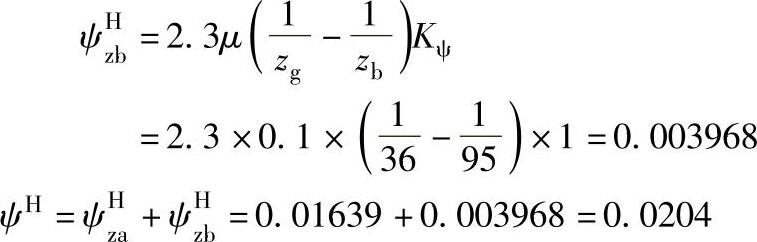
轮b固定时
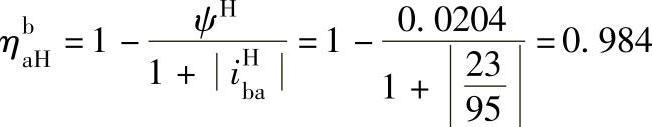
轮a固定时
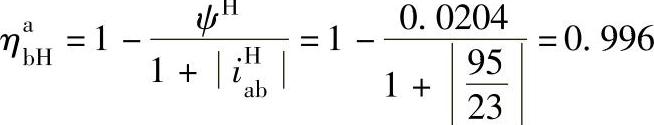
轮a、b主动、行星架H从动时
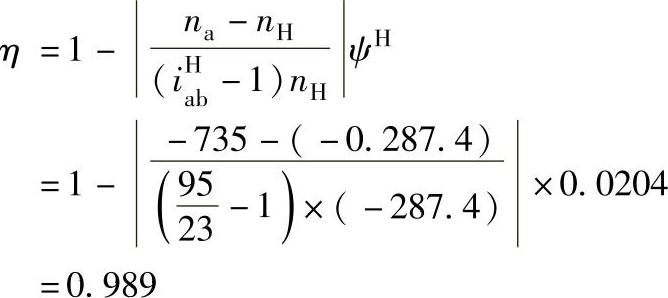
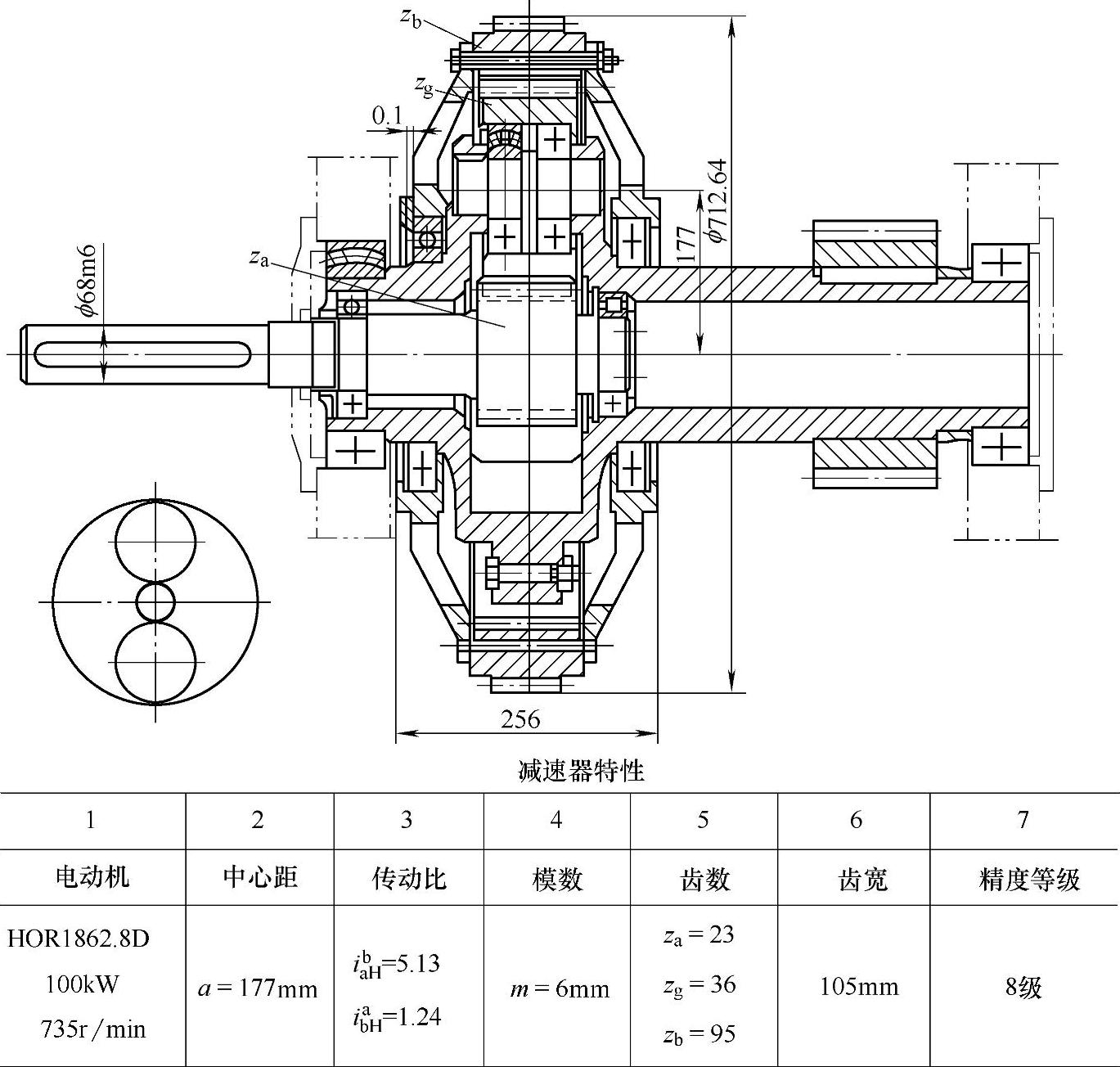
图6-86 100t铸锭吊车主卷扬机行星差动减速器
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




