基本构件与行星轮支承结构设计

1.中心轮和行星架的支承

如果不浮动中心轮和行星架的轴不受外载荷（原动机或工作机械传给的径向和轴向载荷），当行星轮数n_p≥2时，轴承通常是按轴的直径选择轻型或特轻型的向心球轴承。如果轴承受外载荷，则应以载荷大小和性质通过计算确定轴承型号。在高速传动中必须校核轴承极限转速。当滚动轴承不能满足要求时，可采用滑动轴承。滑动轴承结构一般为轴向剖分式，长度与直径之比为l/d≤0.5～0.6。

浮动的中心轮和行星架本身不加支承，但通过浮动联轴器与其相连接的输入轴和输出轴上的支承也应按上述原则选择适合的轴承。

旋转的不浮动基本构件的轴向定位是依靠轴承来实现的，而浮动的基本构件本身的轴向定位可通过齿式联轴器上的弹性挡圈来实现，也可采用球面顶块、滚动轴承（最好是球面调心轴承）来进行轴向定位，这种方法有助于浮动的灵敏性。

2.行星轮的支承

在行星传动机构中，行星轮上的支承所受负荷最大。在一般用途的低速传动和航空机械的传动中采用滚动轴承作为行星轮的支承。在高速传动中滚动轴承往往不能满足使用寿命的要求，所以要采用滑动轴承来支承行星轮。

图6-73所示是常见的采用滚动轴承的行星轮支承结构。为了减小传动装置的轴向尺寸，轴承应直接装入行星轮孔中，但由于轴承外圈旋转，其使用寿命要有所降低（球面轴承除外）。

对于直齿的NGW型传动；行星轮中也可装一个滚动轴承，但该轴承必须要求内外圈之间不能作相对轴向移动，如向心球轴承、球面调心球轴承和球面调心滚子轴承等。对于行星轮为斜齿轮和双联齿轮的情况，不允许装一个滚动轴承，因为行星轮受有啮合力产生的倾翻力矩的作用。

为了减少由制造误差和变形引起的沿齿长载荷分布不均匀，行星轮内装一个球面调心轴承是很有利的（见图6-73f）。但应注意，此时传动中的浮动构件只能有一个，并要计算机构自由度，不能有多余自由度存在。

一般情况下，行星轮内可装两个滚动轴承（见图6-73a、b、c等）。为了避免轴承在载荷作用下，由于初始径向游隙和配合直径的不同而产生行星轮倾斜，预先对轴承进行挑选配对是有必要的。还可将轴承之间的距离L_b加大，以减小这种倾斜，如图6-73b、c所示。

为了使行星轮和轴承之间轴向定位，采用矩形截面的弹性挡圈1（见图6-73a）是最恰当的。避免了在行星轮孔内设置工艺性差的台阶（挡肩）措施。调节环2用于补偿轴向尺寸误差。为增强弹性挡圈抵抗在载荷作用下轴承外圈歪斜的能力，可在挡圈与轴承外圈之间加一不倒角的环3（见图6-73e）。

当行星轮直径较小，装入普通标准轴承不能满足承载能力要求时，可采用专用的轴承，如图6-74a、b、d所示的去掉两个或一个座圈的滚子轴承和滚针轴承的结构。在这种情况下，轴外表面和行星轮内孔可直接作为轴承的滚道（滚道需精磨）。用于这种结构的轴和齿轮常采用合金渗碳钢来制造，以保证硬度为61～65HRC。

在速度较低的行星传动中，还可采用减薄内、外圈厚度，去掉保持架，增大滚动体直径和数量的多排（如三排）专用滚子轴承（见图6-73c），这种轴承的润滑必须充分。

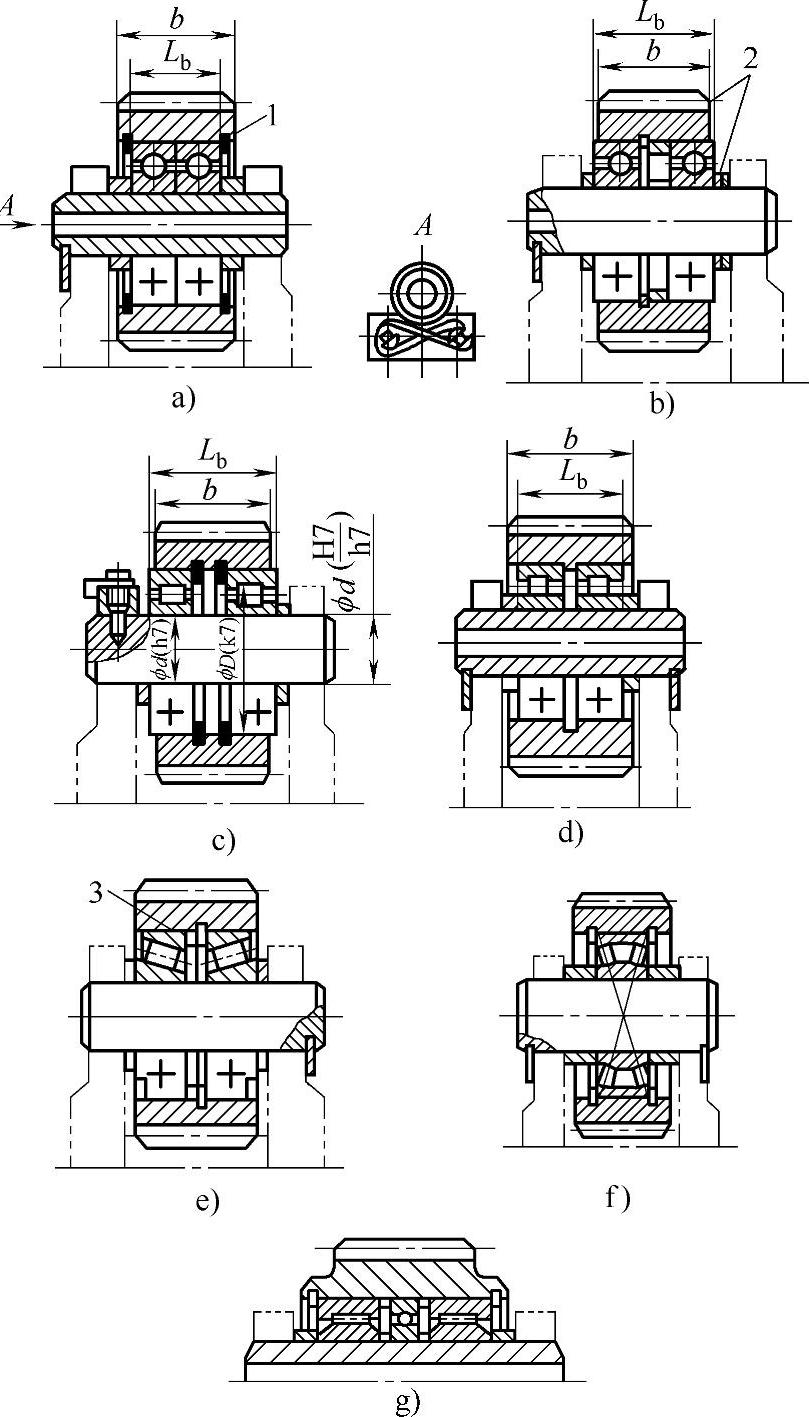
图6-73 轴承装于行星轮体内的结构

将滚动轴承装在行星架上的方法（见图6-75）可以解决因轴承径向尺寸大、行星轮体内无法容纳的困难，这时为了装配的可能性，行星架往往要做成分开式的。这种结构的轴承之间距离较大，由轴承径向游隙不同而引起的行星轮的倾斜将减小。这种支承方式的缺点是结构复杂，轴向尺寸大。

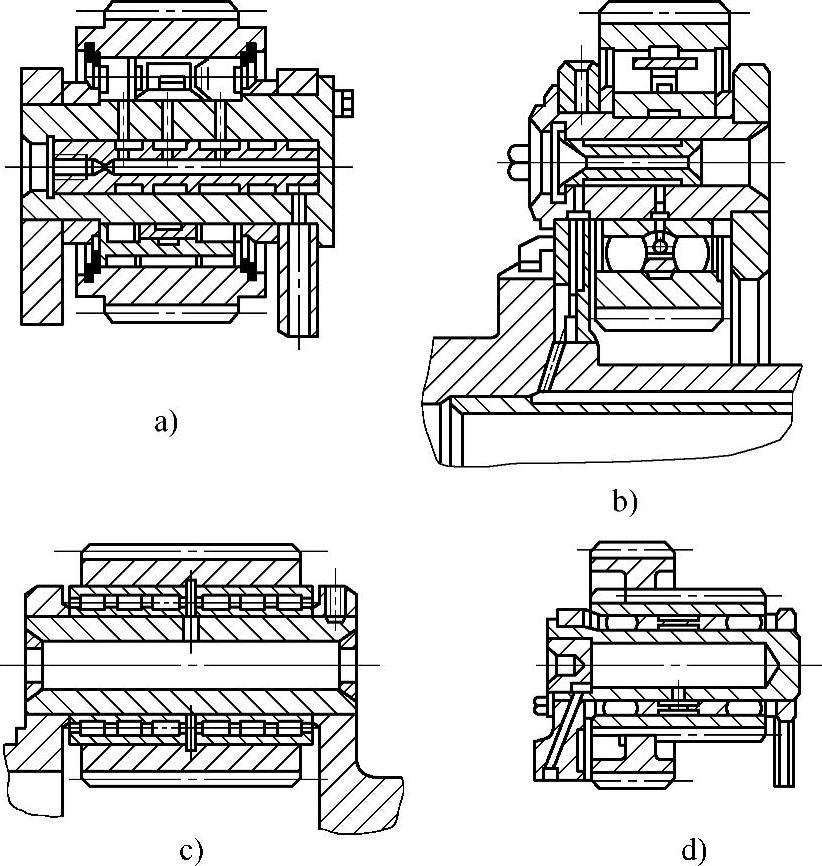
图6-74 采用专用轴承的行星轮支承结构

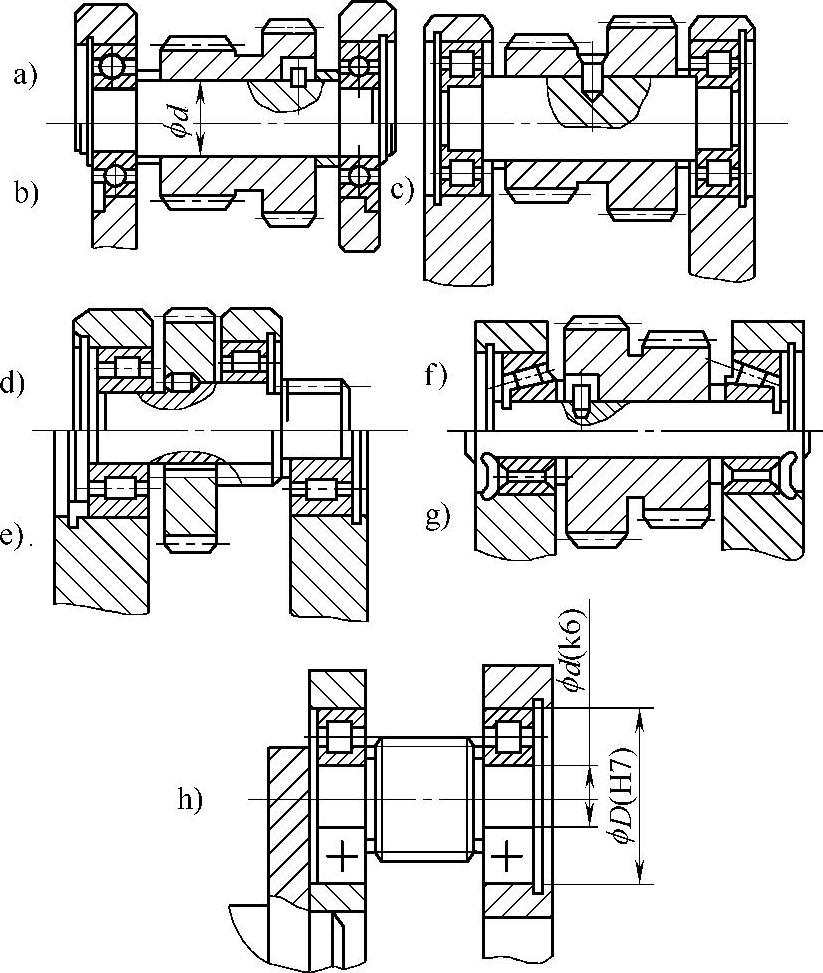
图6-75 轴承装于行星架上的结构

行星轮的支承若采用两个可以轴向调整的轴承（如图6-75f所示的圆锥滚子轴承），则其工作性能取决于轴向调整的准确性。对斜齿轮和双联行星轮来说，因为有倾翻力矩的作用，轴向调整的可能性尤为重要。为简化装配时的调整工作，无特殊需要时，一般应尽量采用不需要轴向调整的轴承，如短圆柱滚子轴承、滚针轴承等。

滚动轴承的内圈与行星轮轴的配合、外圈与行星轮内孔或行星架孔的配合代号在图6-73c和图6_-75h中均有表示。选择配合的原则是，相对于作用在轴承上的力矢量旋转的座圈应配合紧一些，反之配合应松一些。

图6-76所示是被广泛采用的行星轮滑动轴承结构。它的特点是将抗磨材料（巴氏合金）施加在行星轮轴上，而不是在行星轮孔里压入轴承套。行星轮轴上巴氏合金的厚度一般控制在1mm左右，最大不超过3mm。随着巴氏合金的层厚度的增加，其疲劳强度将下降。有时在行星轮轴表面先镀一层铜然后再挂巴氏合金，以使硬度、散热、热膨胀等性能形成一梯度，有利于提高巴氏合金的抗疲劳性能。

由于行星轮内孔表面相对于作用在轴承上的力是旋转的，而行星轮轴是不转的，所以巴氏合金层的挤压是不变的，因而可提高轴承的承载能力和疲劳寿命。另外，这种轴承有利于提高行星轮的精度，因为行星轮是以精加工后的孔作为基准来切齿的。而在行星轮孔中压入轴套的结构，其轴套上巴氏合金层的加工要以轮齿作为定位基准，从而降低了制造精度（如齿圈径向跳动误差增大等）。同时轴套内表面是在变载荷下工作的，故降低了巴氏合金的疲劳强度和寿命。

当滑动轴承的长径比l/d=1～1.5时，可将其分成独立的两段，在每段的中部有导油孔和油沟。对于行星架旋转（包括正反转）的行星传动，导油孔的方向为沿行星架半径方向从行星轮轴中心通向外侧表面（见图6-76b），其油流方向与离心力方向相同。对于行星架不旋转的行星传动，导油孔为行星轮轴上沿行星架半径方向的通孔，即油流可从上、下两个方面同时导入（见图6-76c）。在行星架旋转过程中，导油管起到隔离和滤除杂质的作用。行星轮轴表面上的油沟会降低轴承的承载能力，但它能使油流量增加，促使轴承温升降低。

在高速传动中，计算行星轮滑动轴承时，必须考虑行星轮离心力的影响，通常离心力要大到占轴承总负荷的90%以上。由此可见，高速行星传动空载运行即可考验行星轮轴承的寿命了。离心力F_wg（N）按下式计算

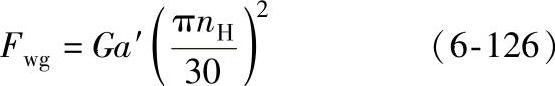
式中 G——行星轮的质量（kg）；

a′——中心距（m）；

n_H——行星架转速（r/min）。

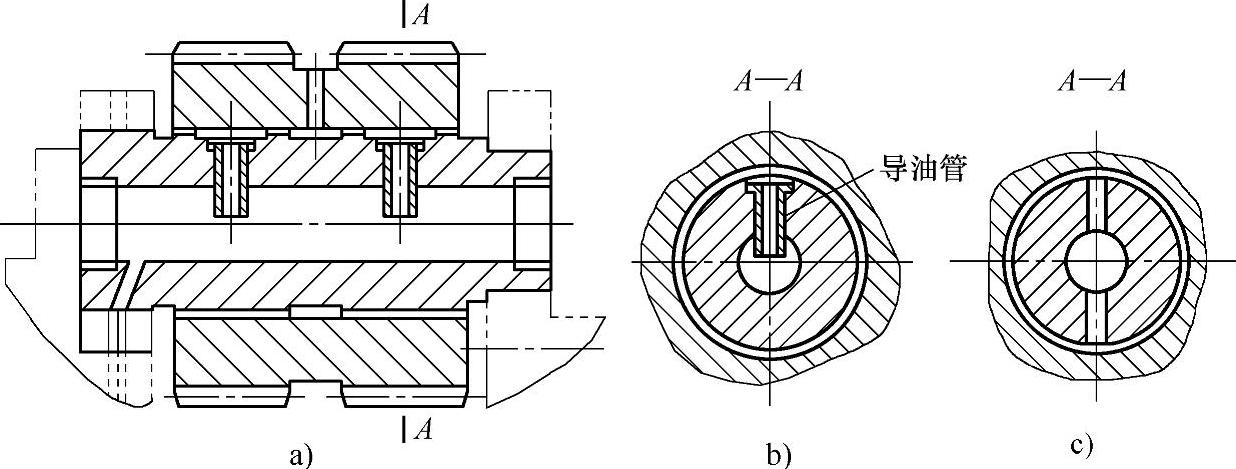
图6-76 行星轮滑动轴承

滑动轴承的比压p（MPa）是影响轴承寿命的一个重要因素，如何减小比压是设计时必须考虑的问题之一。比压的计算如下式

式中 d——轴承直径（mm）；

l——轴承长度（mm）；

F——作用在轴承上总径向力（N），其计算为

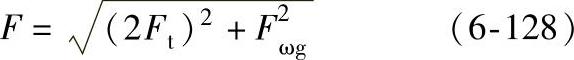
式中 F_t——齿轮啮合处的圆周力（N）；

F_ωg——行星轮的离心力（N）。

从式（6-127）和式（6-128）可知，啮合处的圆周力一定时，要减小比压p必须增大轴承长度l和直径d；减小离心力Fωg而增大l则受齿轮宽度限制，且效果不如增大d好。d增大的同时还减小了行星轮质量，从而减小了离心力，对降低p很有利，但这必须在行星轮轮缘的强度和刚度允许的条件下进行。

根据经验，行星轮内孔直径d（即轴承直径）与分度圆直径d_e之比取为

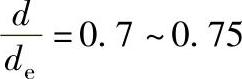
一般情况下，比压最大值为p_max=4.5MPa，常用比压范围：p=3.0～4.0MPa。

比压与轴承滑动线速度之积的允许范围为

[pv]≤100～150MPa·m/s

轴承滑动线速度v（m/s）为

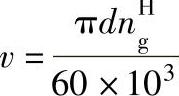
式中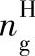——行星轮相对于行星架的转速（r/min）。

对于内齿圈固定的NGW型传动可按下式计算

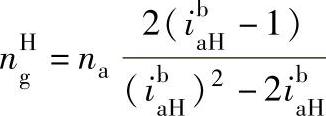
式中 n_a——太阳轮的转速（r/min）；

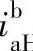——太阳轮至行星架的传动比。

当已知行星轮的绝对转速时，可以直接按其与行星架的转速之差计算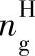。(www.xing528.com)

轴承径向间隙：Δ=（0.002～0.0025）d，速度高、直径小的情况下取大值，反之取小值。

3.行星轮滚动轴承的计算

在已知轴承工作条件、结构形式和给定寿命时间的情况下，按额定动负荷C选择轴承，即

式中 f_p——工作情况系数；

f_p1——负荷性质系数，见表6-27；

f_p2——齿轮系数，见表6-28；

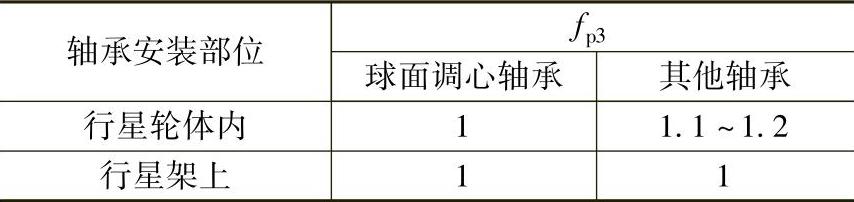
f_p3——安装部位系数，见表6-29；

f_t——温度系数，对齿轮传动取f_t=1；

f_h——寿命系数；

f_n——速度系数；

p——当量动负荷（N）。

表6-27 负荷性质系数fp1

表6-28 齿轮系数fp2

表6-29 安装部位系数fp3

f_h和f_n可从轴承手册中查取，或按下式计算

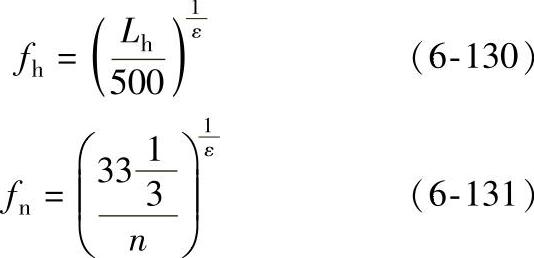
式中 n——轴承转速（r/min），；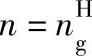

L_h——轴承额定寿命（h）；

ε——寿命指数，对球轴承ε=3，对滚子轴承。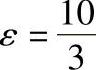

当量动负荷可按实际工作负荷的性质确定。因为行星轴承一般只承受径向负荷，轴向负荷可忽略不计（个别情况下采用圆锥滚子轴承及单斜齿NW型传动除外），所以在外载荷大小和转速不变的情况下，有

p=F_1p（6-132）

F_1p为作用于一个轴承上的径向负荷，可查有关资料确定。对于NGW型传动也可按下式计算

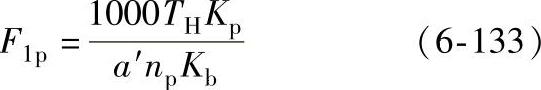
式中 T_H——行星架传递的转矩（N·m）；

a′——中心距（mm）；

K_b——单个行星转上的轴承数；

K_p——行星轮间的载荷不均匀系数。

当轴承在负荷和速度变动情况下工作时，当量动负荷p应以平均当量动负荷p_m代入。假定轴承依次在当量动负荷p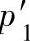、、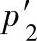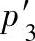…作用下运转，其相应的行星轮相对转速为n₁、n₂、n₃…在每种工况下运转的时间与总运转时间之比为q₁、q₂、q₃…，如图6-77所示，则平均动负荷为

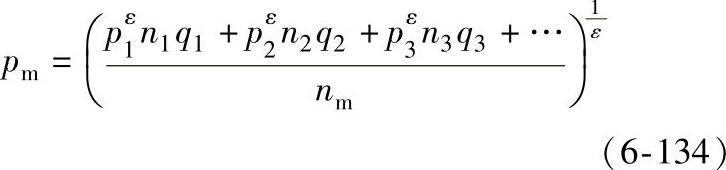
n_m=n₁q₁+n₂q₂+n₃q₃+…

式中 n_m——平均转速。

如果轴承转速大小和负荷方向保持不变，当量动负荷在p_min和p_max之间线性变化（见图6-78），其平均动负荷按下式计算

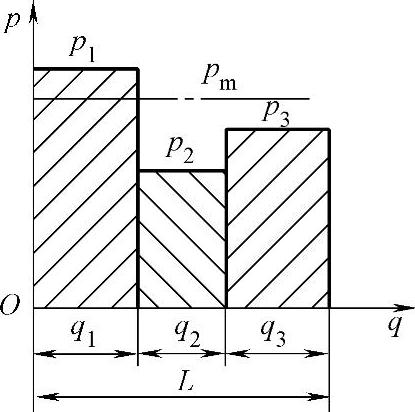
图6-77 负荷与转速变化时平均当量动负荷

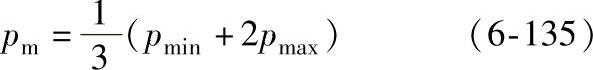
当行星轮的离心力不可忽略时，必须按合成当量动负荷计算。NGW型的合成当量动负荷为

或

在行星传动装置设计中，也可根据经验和结构情况先选择比较合适的轴承型号，然后进行寿命校核计算，即按下式求出寿命系数

再以f_h从轴承手册中查取或按下式计算额定寿命时间L_h（h），即

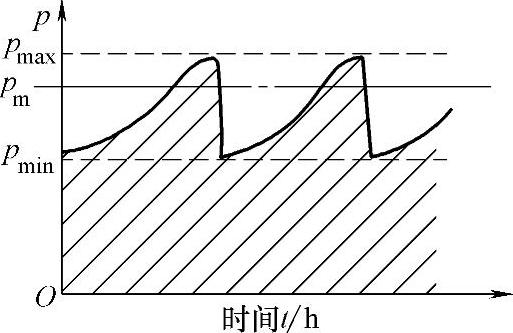
图6-78 转速不变时的平均当量动负荷

行星传动中滚动轴承的额定寿命可参考表6-30选定。一般应保证轴承能工作三年以上，如确因条件限制，则最少也要保证工作一年到一年半。对于那些要求绝对可靠的场合，L_h可取比表中更大的数值。

表6-30 行星轮轴承额定寿命Lh

对于NGW型传动，当轴承装在行星轮内时，合理的轮缘柔性和轴承径向间隙，可改善轴承中滚动体之间的载荷分配情况，有利于提高轴承的寿命，这是值得注意的因素。