齿轮结构的设计与计算方法

1.太阳轮

1）结构特点。太阳轮的结构随其传动类型、是否浮动及浮动方式的不同而不同。

在行星齿轮传动中，通常有三个以上的行星轮对称布置。太阳轮上的横向力，在有均载措施的情况下基本平衡，取K_p≈1。所以太阳轮的轴不存在抗弯强度方面的问题。

2）柔性轮缘的强度计算。图6-47所示为太阳轮轮缘强度计算简图。太阳轮结构可简化为受内、外载荷的封闭圆环，其弯曲半径与断面厚度之比ρ/h＜5，属于大曲率圆环，弯曲中性层与重心不重合，相距为e。轮缘强度计算公式见表6-18。

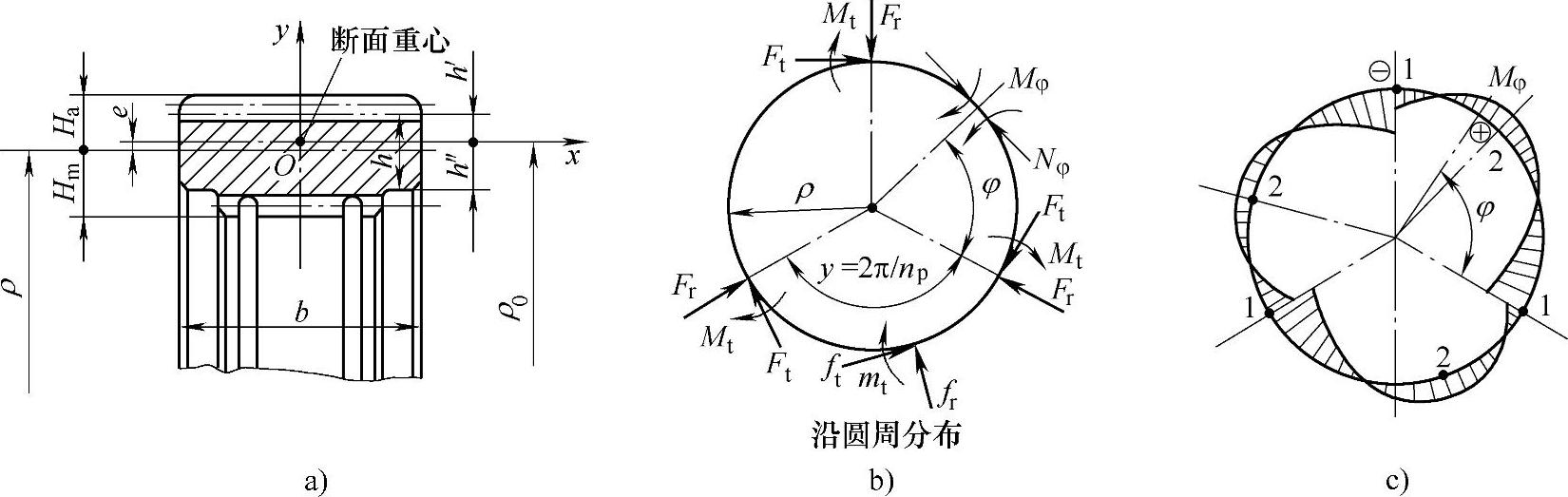
图6-47 太阳轮轮缘强度计算简图

a）断面参数 b）计算简图 c）弯矩分布

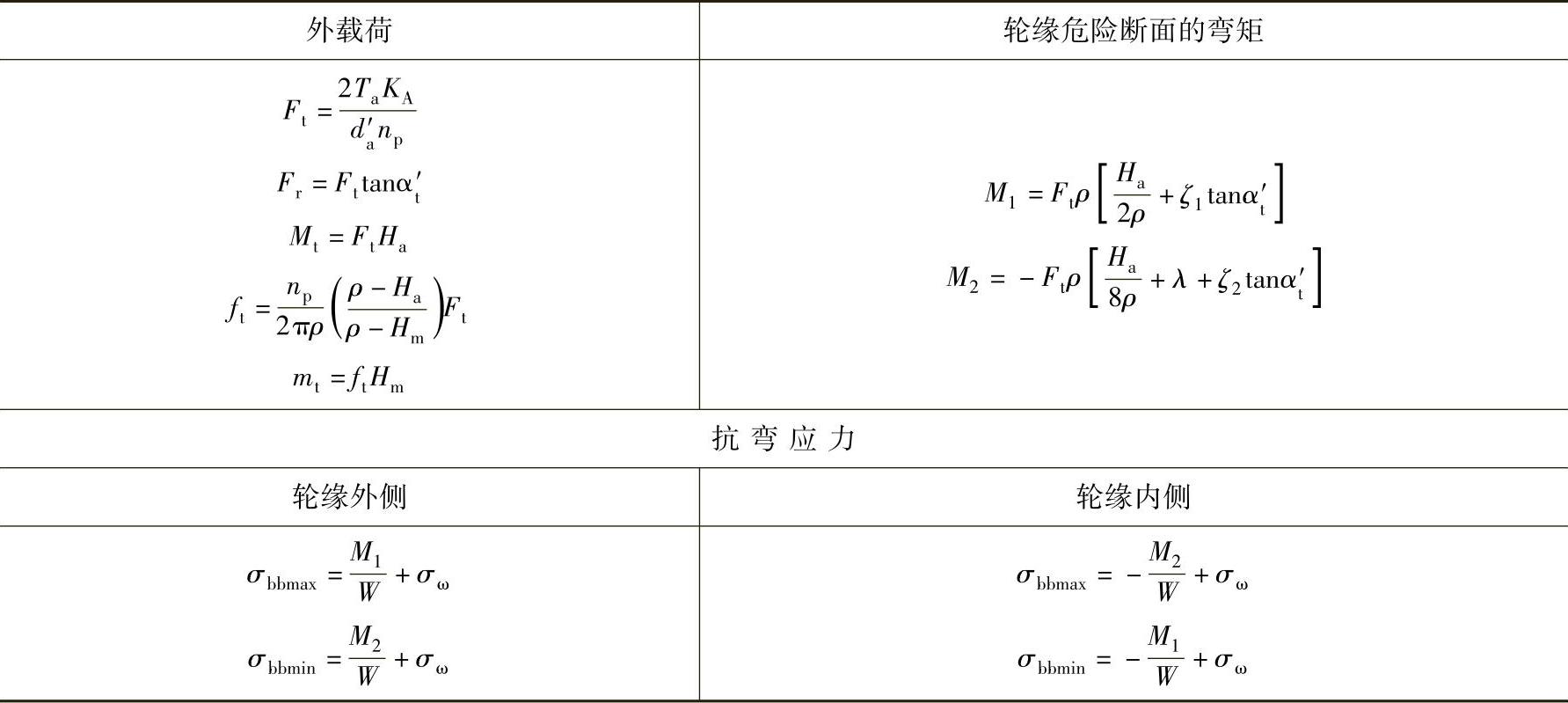
表6-18 太阳轮轮缘强度计算公式

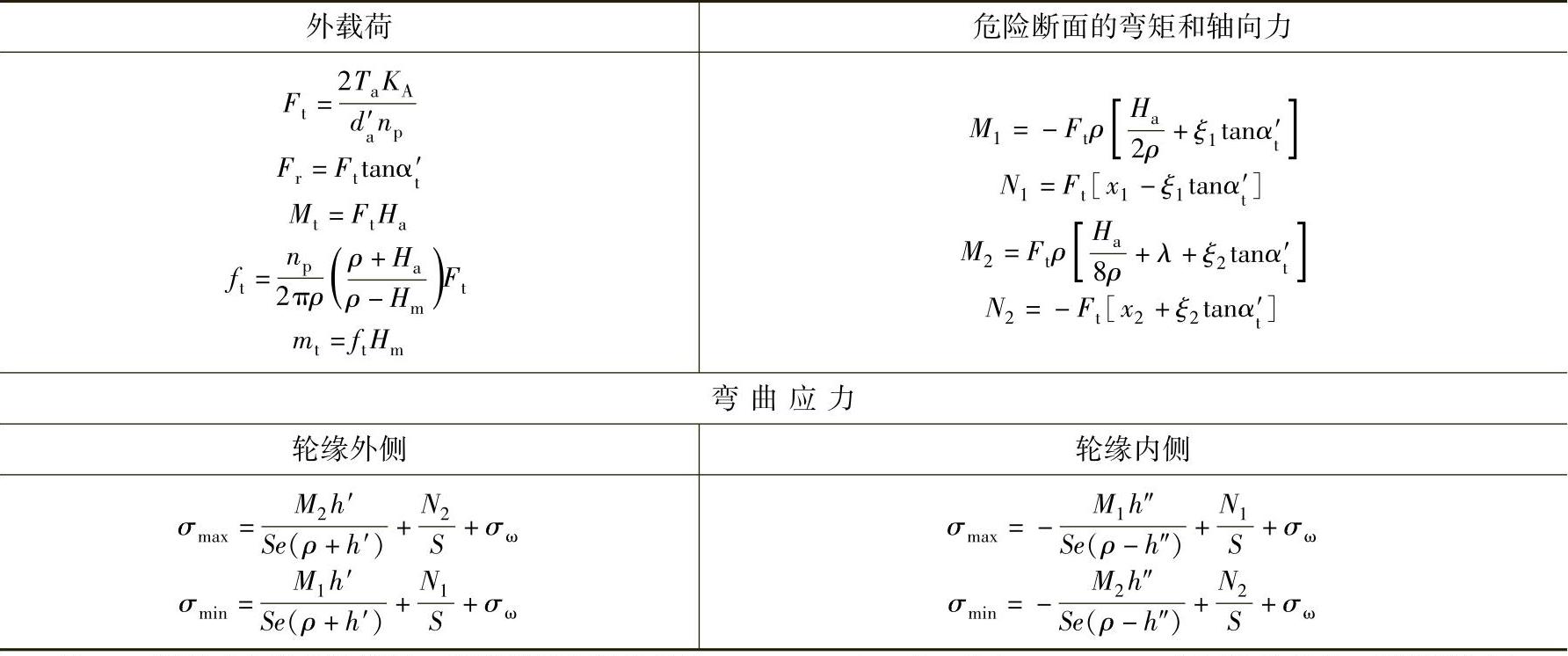
注：1.使用表中公式计算时，相当断面的惯性矩为：I=I_min+S_mina²。式中，I_min、S_min为不计轮齿时，实际断面为Ox轴的惯性矩和断面面积；a为系数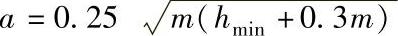，（h_min为不计轮齿时的断面厚度，m为齿轮模数）。

2.相当断面的宽度取轮缘的实际宽度b，其高度h、面积S、抗弯截面模量W分别为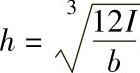；S=bh；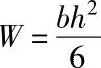

3.轮缘断面的曲率半径为ρ=ρ₀-e。式中，。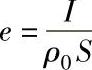

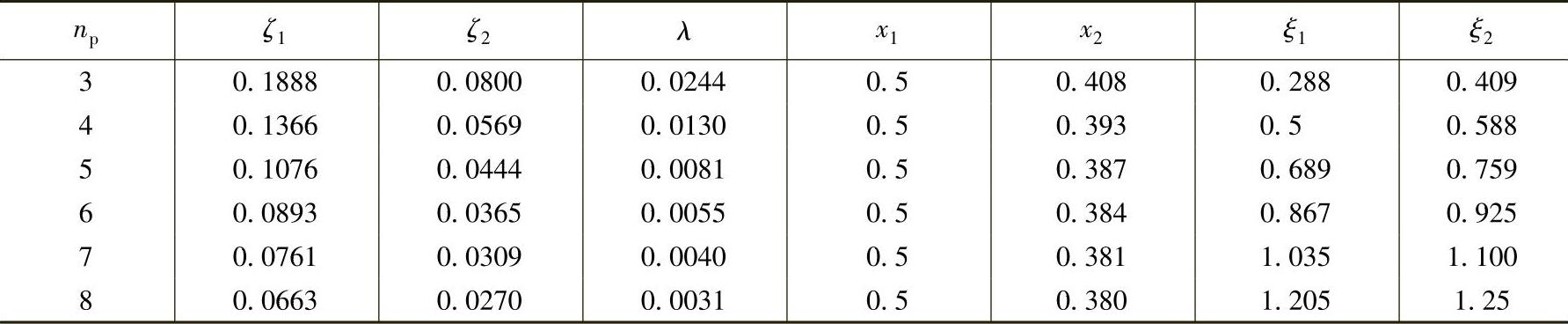
4.系数ζ₁、ζ₂、x1、x2、λ、ξ1和ξ2按表6-19确定。

5.T_a为太阳轮总转矩；K_A为使用系数；F_t为K_p=1时太阳轮上的圆周力。

6.H_a为太阳轮圆周力的力臂，对于β=20°～30°的斜齿轮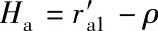，；对于直齿轮或β＜20°的斜齿轮，H_a=r_a1-ρ。式中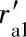，和r_a1分别为太阳轮的节圆半径和顶圆半径。

7.σω为离心力引起的应力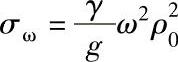，。式中，γ为齿轮材料密度；g为重力加速度；ω为齿轮的绝对角速度；ρ0为轮缘断面重心位置的曲率半径。

表6-19 太阳轮和行星轮轮缘几何系数

2.内齿轮

1）结构特点。内齿轮的结构随其是否旋转、浮动及浮动方式的不同而不同。在内齿轮结构设计中，必须考虑插齿时的退刀槽和插齿刀最小外径d_a0所需要的空间尺寸。具体规定应按有关标准执行。

2）柔性轮缘的强度计算。图6-48所示为内齿轮轮缘强度计算简图。其弯曲半径和断面厚度之比ρ/h＞5，属小曲率圆环，弯曲中心与断面重心可认为重合。轮缘强度计算公式见表6-20。

3）柔度计算。对于图6-48所示的内齿轮轮缘强度计算简图，若以节点在啮合线方向上的位移δ表示内齿轮的变形，以δ与轮齿单位宽度上的载荷q之比表示轮缘的柔度，则

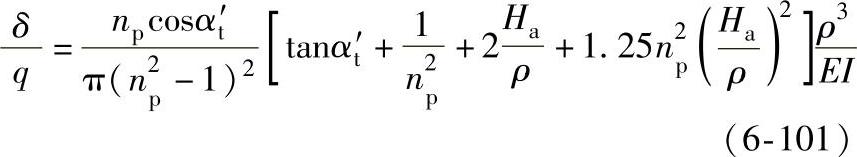
按上式计算，设开始运转时，仅有一半行星轮参与啮合，其柔度急剧增大，按表6-21选取轮缘断面尺寸时

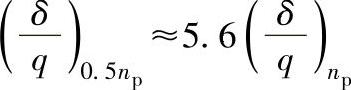
表6-20 内齿轮轮缘强度计算公式

注：1.表中系数ζ₁、ζ₂和λ按表6-19确定。

2.表中仍以相当矩形断面计算应力。相当断面对Ox轴的惯性矩为：I=I_minK。式中，I_min为不计轮齿时的断面惯性矩；K为计算系数，按图6-49确定。图6-49中I_max为包括全齿高在内作为实体断面计算的惯性矩（不计浮动齿）。

3.相当断面的宽度b、高度h、面积S、抗弯截面模量W的计算和太阳轮算法相同。

4.内齿轮轮缘的曲率很小，可取曲率半径ρ≈ρ₀，横向力的影响小而忽略不计。

5.H_a和离心力引起的应力σω，其意义和计算方法同表6-18注6、7。

表6-21 浮动内齿轮的轮缘断面尺寸

注：适用于调质硬度为280～320HBW的合金钢轮缘。

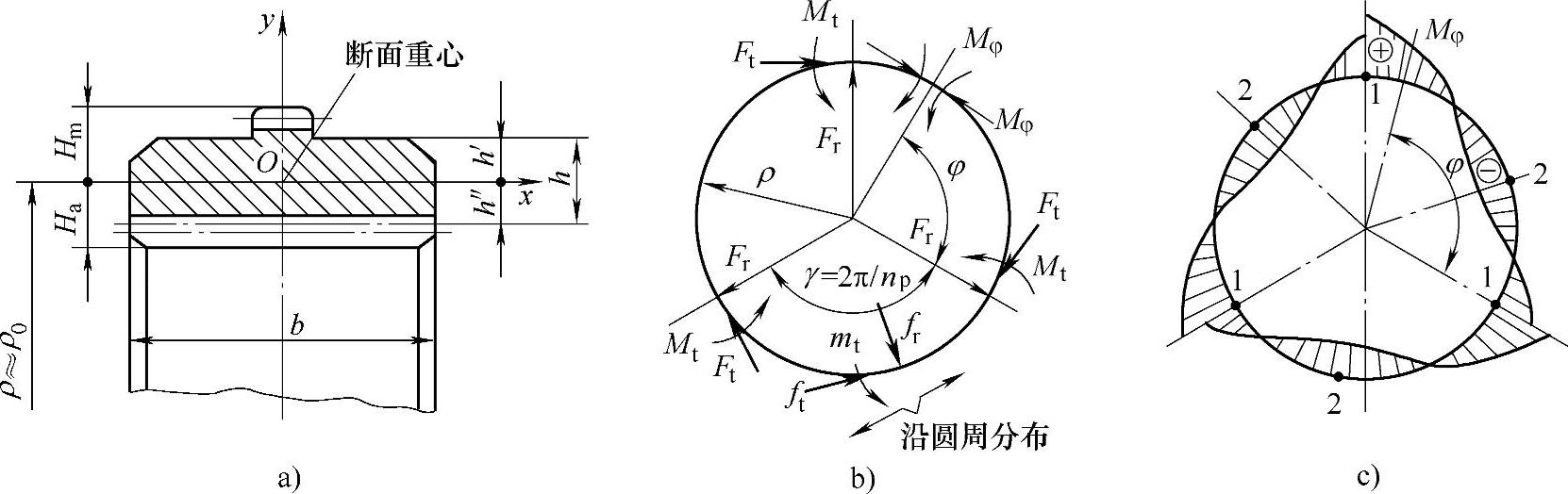
图6-48 内齿轮轮缘强度计算简图

a）断面几何尺寸 b）计算简图 c）弯矩分布

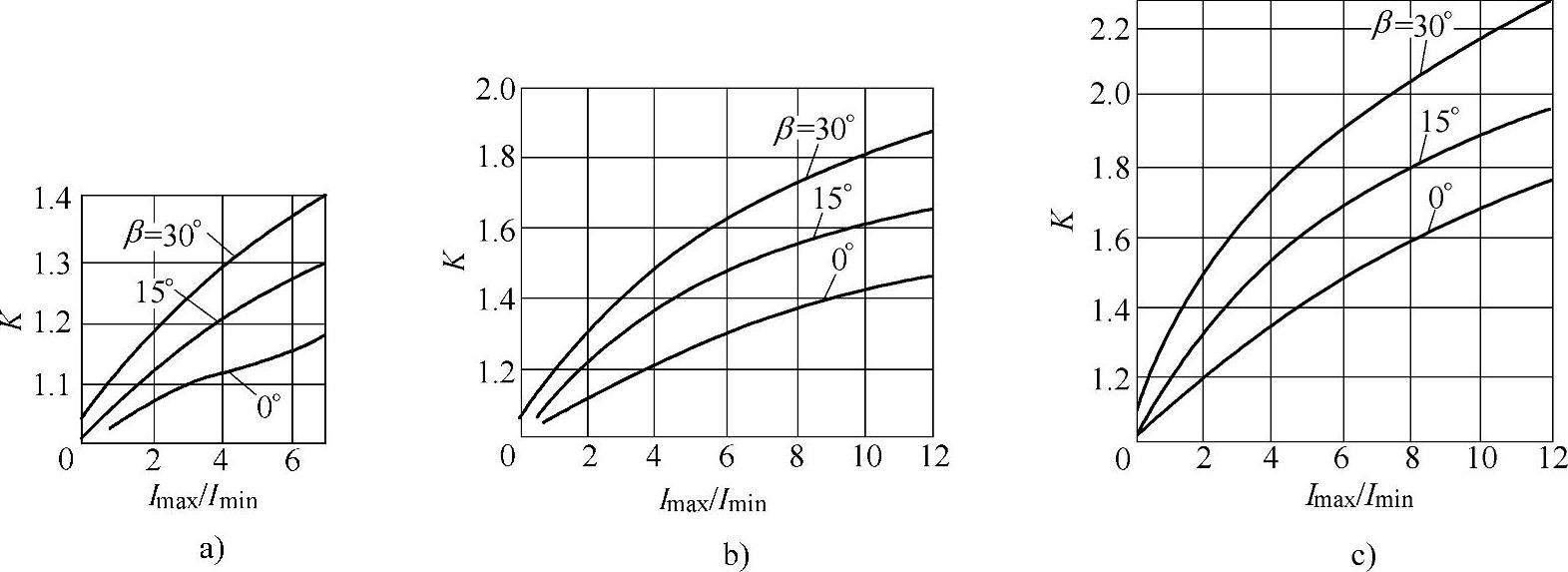
图6-49 内齿轮轮缘断面惯性矩计算系数K

a）m_n=2mm b）m_n=5mm c）m_n=8mm

可见，合理设计内齿轮轮缘断面和尺寸，对提高行星传动的承载能力很有好处。

按式（6-101）计算，符合表6-21中断面尺寸关系的内齿轮柔度与行星轮数的关系如图6-50所示。图中虚线为刚度系数C=14500N/mm²时轮齿的柔度。

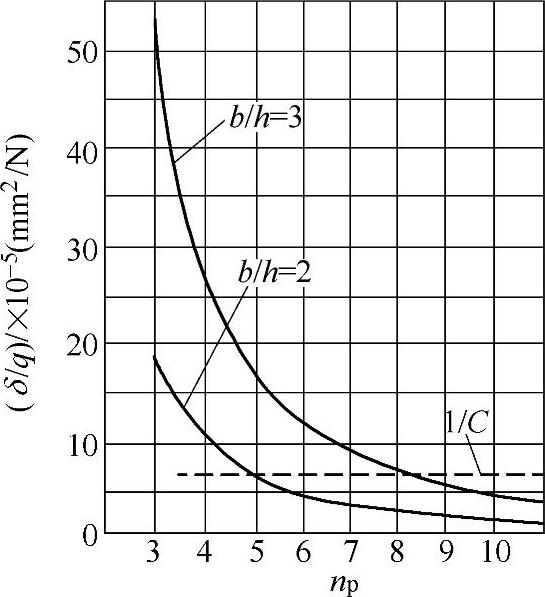
图6-50 内齿轮柔度与行星轮数的关系

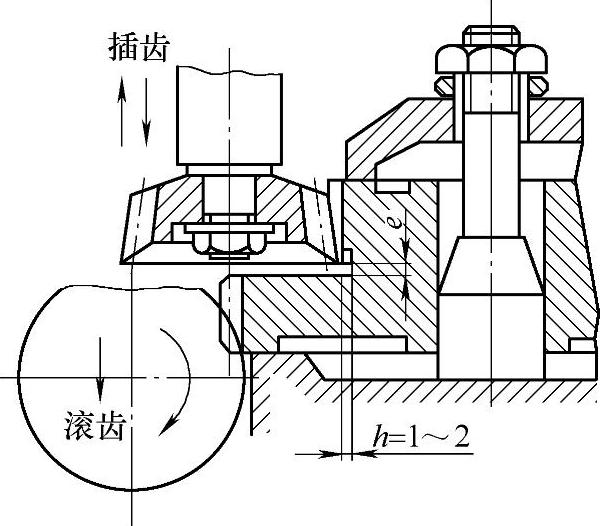
图6-51 整体式双联行星轮结构及加工方式

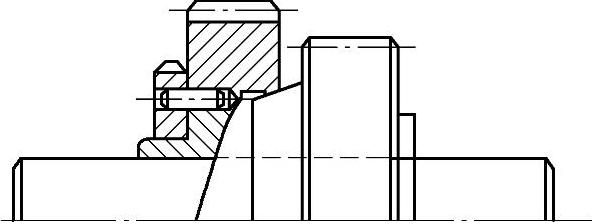
图6-52 装配式双联行星轮结构

3.行星轮

1）结构特点。行星轮多作成中空齿轮或双联行星轮。对于双联行星轮，如图6-51和图6-52所示，无论是整体式还是装配式，同一传动中行星轮上两齿轮的位置关系必须准确一致，否则将会严重影响行星轮之间的载荷均衡，甚至根本不能运转。

高速传动中，行星轮的质量必须相对于自身轴线平衡，装在同一传动中的行星轮的质量应严格一致，以保证行星架装配件的工作平衡性。(www.xing528.com)

2）轮缘强度计算。图6-53所示为行星轮轮缘强度计算简图。行星轮也属大曲率圆环，当轴承装在行星轮内时，若h/m＜3，假设轴承支反力按余弦规律分布（见图6-53b），并且不考虑离心力对轴承载荷的影响（仅指中、低速行星传动），其简化计算公式见表6-22。

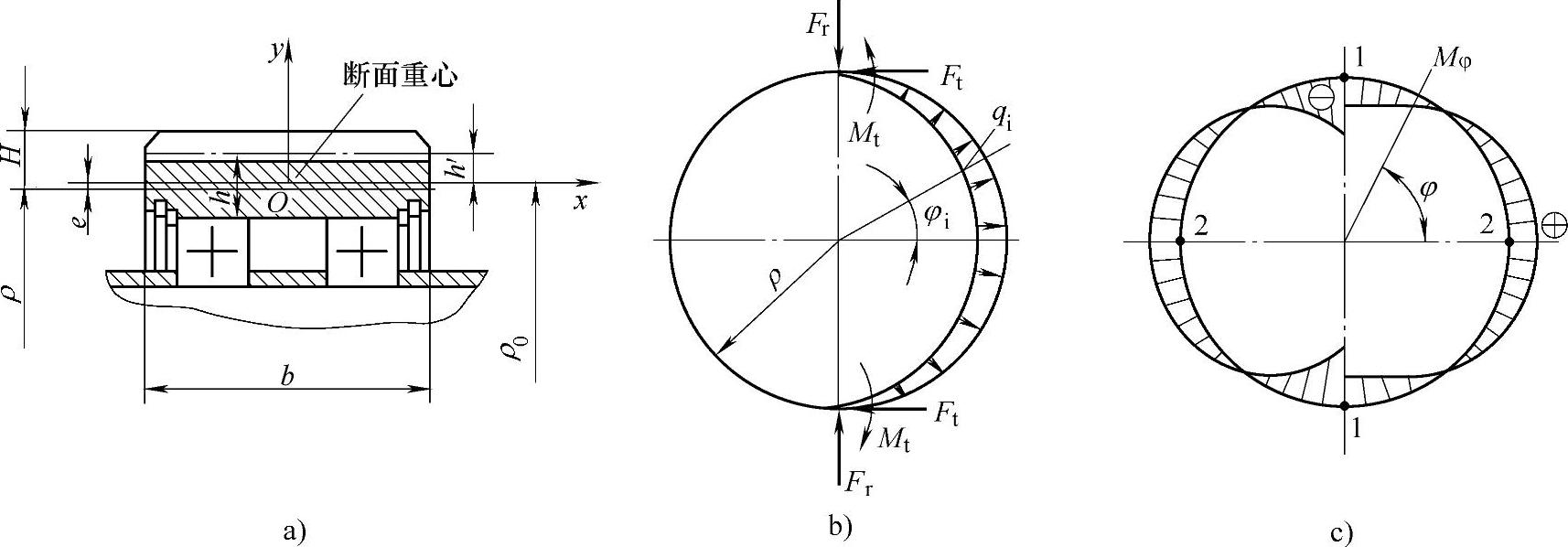
图6-53 行星轮轮缘强度计算简图

a）断面几何参数 b）计算简图 c）弯矩分布

表6-22 行星轮轮缘强度简化计算公式

注：表中代号意义及其计算同表6-18注。

4.太阳轮、内齿轮轮缘疲劳强度校核

行星齿轮传动中，齿轮轮缘内、外侧任一点上的应力，都在σ_max和σ_min之间变动，且为交变应力，故其强度计算以校核疲劳安全系数为宜。对于太阳轮，一般只进行弯曲疲劳屈服极限校核。当齿轮传递转矩在轮缘内产生很大的切应力时，应进行扭转强度极限校核。其安全系数Sσ和Sτ分别按下式计算

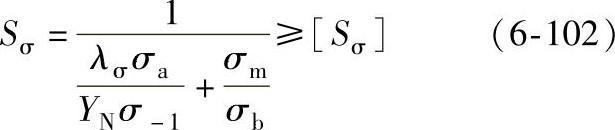
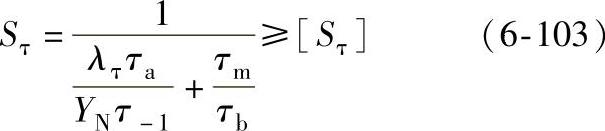
式中 σ_b、τ_b——齿轮材料的抗拉强度和抗剪强度，对于近似计算，可取τ_b=0.68σ_b。

σ_-1、τ_-1——齿轮材料的弯曲和扭转对称循环疲劳极限，一般取σ_-1=0.43σ_b，τ_-1=（0.54～0.6）σ_-1；

σ_a、τa——正应力和切应力的应力幅：σ_a=，；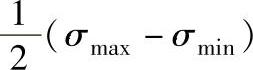

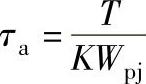T——太阳轮上作用的转矩；

W_pj——扭转净抗弯截面系数；

K——考虑应力循环特性的计算系数，K=1（对称循环）或K=2（脉动循环）；

σ_m、τ_m——正应力和切应力的平均应力：

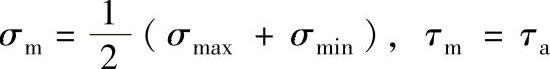
（脉冲循环）或τ_m=0（对称循环）；

Y_N——寿命系数，与材料种类、硬度和应力循环次数N_L有关，当齿面硬度≤350HBW时

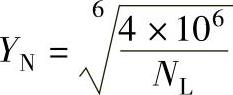
当齿面硬度＞350HBW时

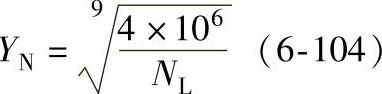
当循环次数N_L＞4×10⁶时，取Y_N=1；计算结果Y_N＞1.7时，取Y_N=1.7；对于扭转计算，一般取N_L等于整个使用期间的起动次数；

[S_σ]、[S_τ]——许用安全系数，当只进行弯曲计算时，一般取[Sσ]≥2，当太阳轮轮缘要同时校核扭转时，可按下式计算总安全系数S值

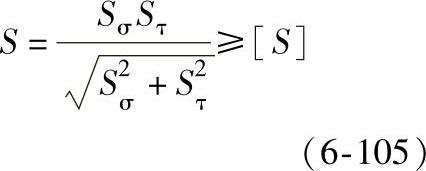
一般取[S]=1.6～2。当材料性能可靠、载荷计算准确时，可取[S]=1.3～1.5。

λ_σ、λ_τ——材料的对称循环极限应力对实际轮缘的折算系数，按式（6-106）、式（6-107）计算

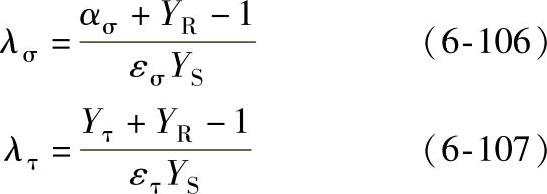
式中 α_σ——弯曲有效应力集中系数，当齿轮材料的σ_b＞750MPa时，取ασ=ασ0，ασ由图6-54和图6-55确定（借用轮齿弯曲疲劳计算资料），图中s_f/ρ_f为齿根厚度与过渡曲线半径之比；

Y_τ——扭转有效应力集中系数，Yτ按表6-23查取；

Y_R——表面粗糙度系数，见表6-24；

Y_S——表面强化系数，见表6-25；

ε_σ、ε_τ——绝对尺寸系数，见表6-26。

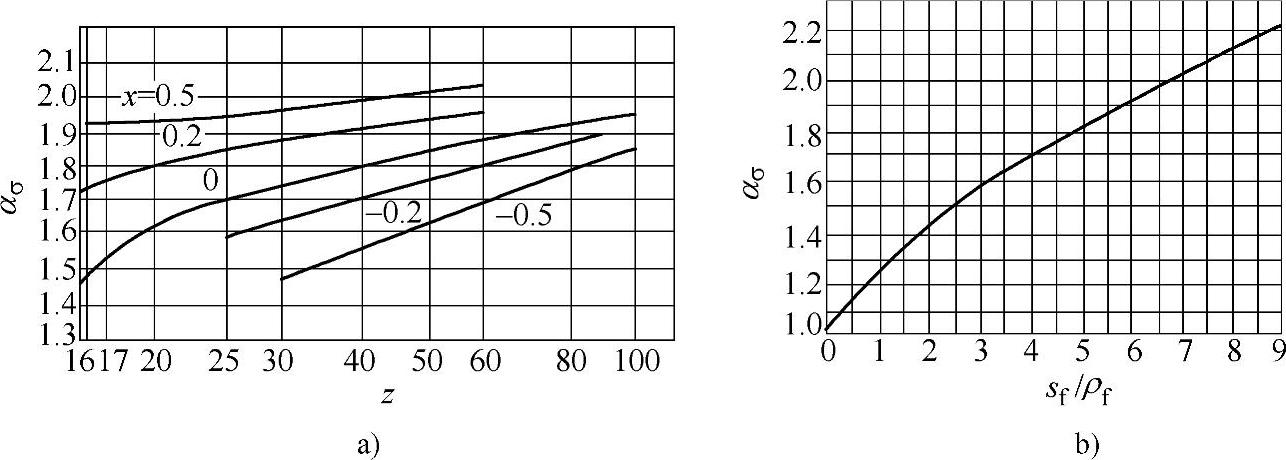
图6-54 直齿外啮合齿轮（α=20°、c∗=0.25）齿根弯曲有效应力集中系数

a）ασ与齿数z、变位系数x的关系 b）ασ与s_f/ρ_f的关系

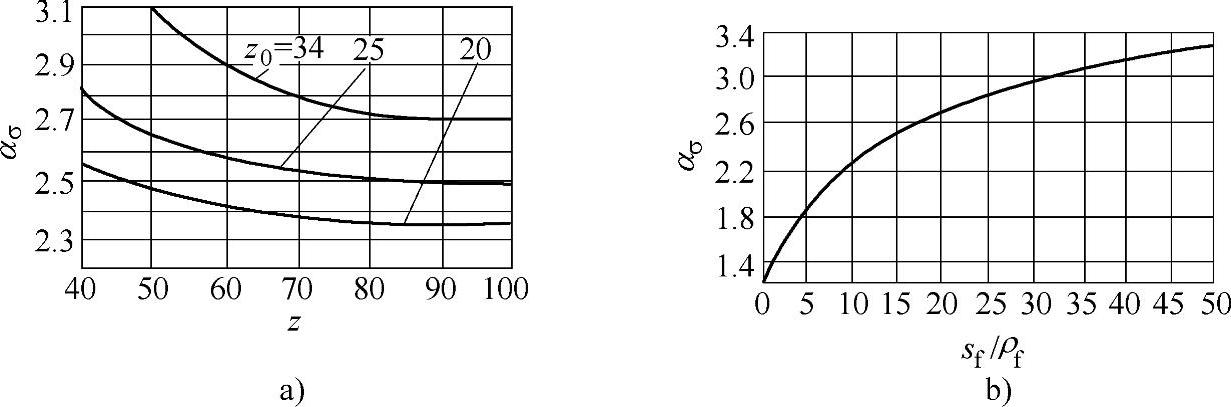
图6-55 内齿轮（α=20°、c∗=0.25）齿根弯曲有效应力集中系数

a）ασ与齿轮齿数z、刀具齿数z₀的关系 b）ασ与s_f/ρ_f的关系

表6-23 扭转有效应力集中系数Yτ

表6-24 弯曲和扭转时的表面粗糙度系数YR

表6-25 表面强化系数YS

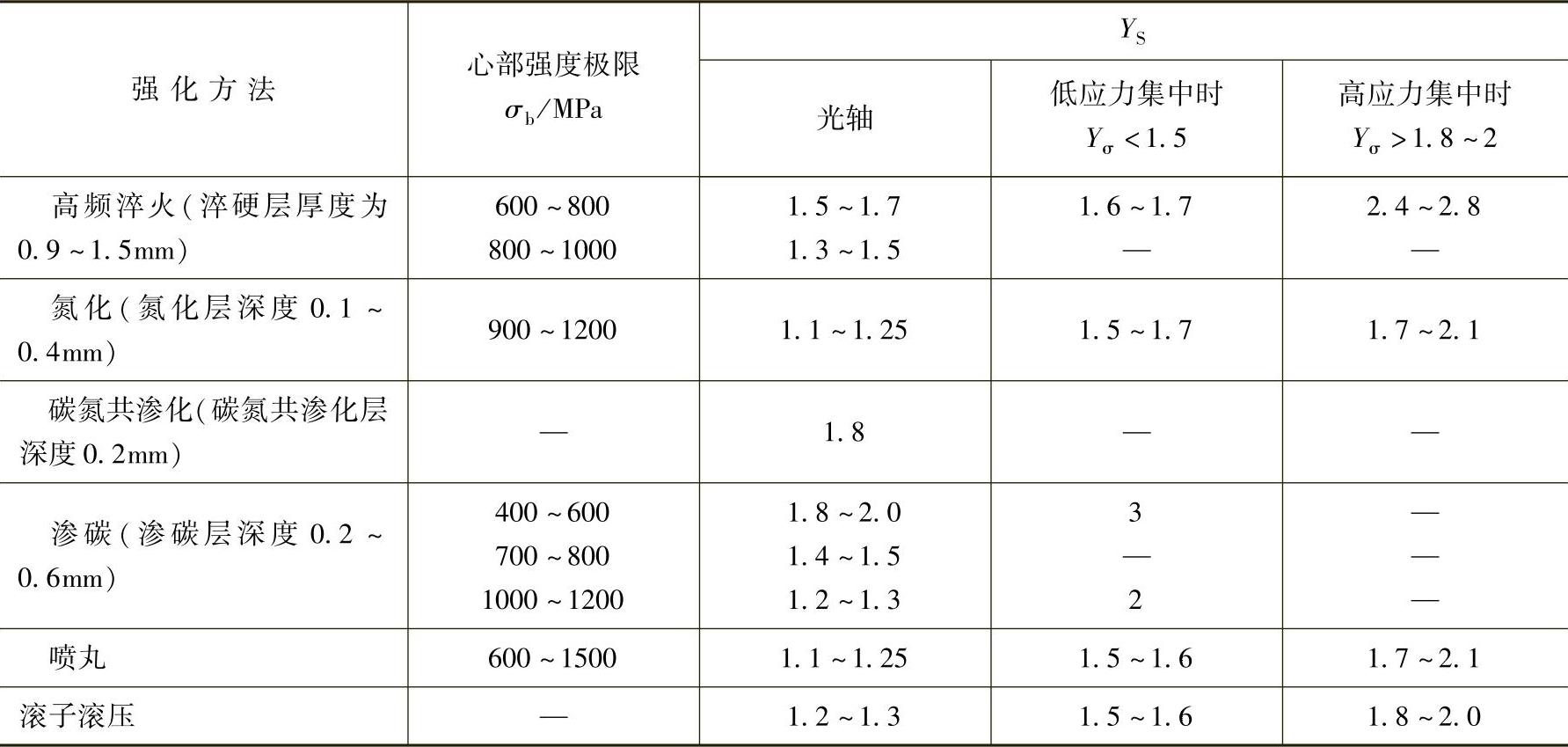
表6-26 绝对尺寸系数εσ和ετ

注：断面尺寸为应力集中处的最小尺寸。