油膜浮动均载装置：优化设计方案

行星轮利用滑动轴承动压油膜弹性达到各行星轮间的均载。与其他均载机构相比，具有均载效果好、结构简单、减振等优点，因而受到世界各国的普遍重视。

中间环共转轴承是套在行星轮轴上与行星轮转速相同的轴承，其形成内层普通轴承和外层共转轴承。每个轴承都可看做具有一定刚性的弹簧，它可作均载机构，可使浮动量增大，其浮动量大于单层普通径向滑动轴承组成的均载机构，因而均载效果更好。现就共转轴承油膜的动压表达式及其形成油膜动压的主要因素作论述。

（1）行星轮中间浮环共转轴承均载机构的结构与作用力 如2K-H（NGW）型行星传动中，运动由太阳轮z₁输入，通过行星轮z₂带动行星架H运动，其转速分别为ω₁、ω₂（见图6-38）。

图6-39所示为目前通常采用的行星轮中间浮环共转轴承的结构。中间浮环端部有模数及齿数都与行星轮相同的齿轮，与太阳轮啮合，从而具有与行星轮相同的转速，实现中间浮环与行星轮的共转。中间浮环与行星轮及行星轮轴之间形成内外两层油膜，从而得到两个径向滑动轴承，内层为普通轴承，外层为共转轴承。

图6-38 2K-H（NGW）型行星轮系简图

图6-39 行星中间浮环共转轴承的均载机构

a）、b）行星轮用滚动轴承 c）行星轮用滑动轴承

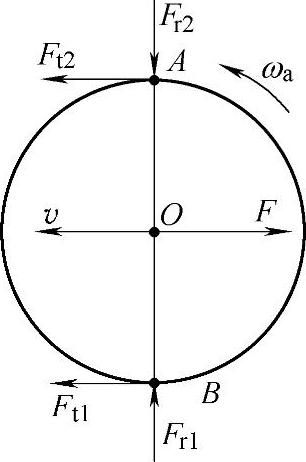
图6-40 行星轮速度和受力分析

对于通常的行星轮系来说，其行星轮的速度和受力分析如图6-40所示。F_r1、F_t1分别为太阳轮作用于行星轮上的径向力及切向力，F_r2、F_t2为内齿圈作用于行星轮上的径向力及切向力，F为行星架对行星轮中心的反力，v为行星轮中心随行星架一起运动的速度，ω₂为行星轮的绝对转速。分析表明，若A、B两处的啮合角相等，则行星轮中心的运动速度v与反力F方向相反。

（2）共转轴承油膜的压力表达式 在油膜浮动的均载机构中，外层共转轴承有其特殊性，这里只分析外层共转轴承。

在很多情况下，行星轮共转轴承的长径比大于1。为了分析形成油膜动态的原因，采用无限长径向轴承的雷诺方程，其表达式为

式中右端第一项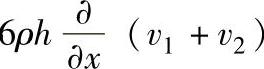，表示轴承两个表面切向速度沿x方向变化时，将产生油膜压力。由于行星轮中心以一定的线速度运动，轴承表面切向速度沿x方向是变化的（其分析可见图6-44）。式中第二项为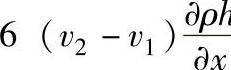，表示轴承两个表面有切向速度差并带动油膜从大口流向小口时，将产生油膜压力，称该项为油楔项。第三项为12ρ（ω₁-ω₂），表示两个表面有法向相对运动时，将产生油膜压力，称其为挤压项，各运动参数方向如图6-41所示。

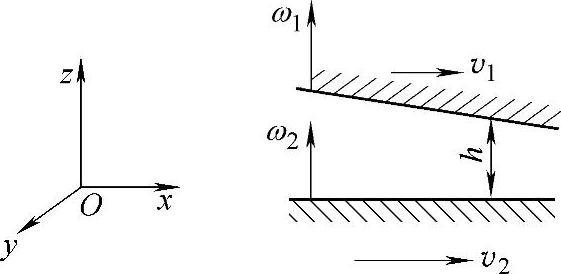
图6-41 雷诺方程的参数

对于行星轮系共转轴承油膜，轴套和行星轮都以ω₂的速度转动，但它们的中心以相同速度ω_H绕太阳轮作公转，以行星轮轴作为参照坐标系，则它们相对于行星轮轴的转速为ω=ω₂-ω_H。同时，轴套和行星轮中心都以速度v一起运动，外载荷F方向与速度v方向相反，以图6-42所示θ=0的直线作参考，外载荷方向与θ=0线的夹角为φ。由于行星轮系中各运动元件的制造和安装误差，使行星轮所受外力的大小随时间而变化，外力方向与行星轮轴运动方向的夹角也随时间变化，以行星轮轴作为参照坐标系，轴套中心相对于行星轮中心的切向和径向运动速度分别为和，c为半径间隙（mm）。对于图6-42中的θ角，所对应的轴承两个表面上的两点M₁、M₂都有切向和法向速度分别为v₁、v₂、ω₁、ω₂。

图6-42 共转轴承的速度分析

图6-43 β与θ的关系

O′—行星轮中心 O—中间浮环中心

已知轴承半径为r，设x=rθ，OO′与O′M₁的夹角为β，则β与θ的关系如图6-43所示，α=θ-β，O′O=e，O′M₁=r。

从而得到图6-42中各速度分量为

得

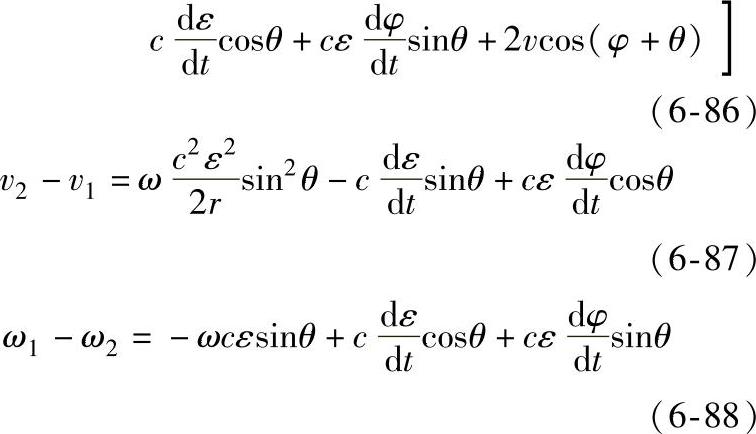
式（6-86）中不等于零，意味着轴套外表面和行星轮内表面速度之和沿x方向有变化，即沿着轴承的圆周方向有变化，其原因可用图6-44所示的轴承来说明。当轴径中心以速度v运动，同时轴径绕中心O点以速度ω转动时，A点切向速度为rω，而B点的切向速度为rω-v，切向速度沿圆周方向是变化的。

图6-44 轴承表面切向速度的变化

设润滑油密度ρ、粘度η均为常数。油膜厚度h=c（1+εcosθ），将以上各式乘以雷诺方程右端第一、二、三项各自的系数，得

为了考察在形成油膜压力的过程中，哪些因素起主要作用，将各项进行比较分析如下：

1）在一般情况下，径向轴承的c/r为10^-3数量级。比较式（6-90）和式（6-91），发现两式右端括号内的多项式后两项的数量级相同，但式（6-90）右端括号内的第一项是式（6-91）对应项的10^-3数量级。因此，式（6-90）右端括号内多项式的数量级不高于式（6-91）括号内多项式的数量级，而式（6-90）与式（6-91）括号前面的系数相差10^-3数量级，因此忽略油楔项的影响，近似为零，即

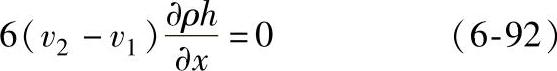
2）考察方程式（6-89），右端多项式中v=aω_H，其中a为行星轮与太阳轮的中心距，ω_H为行星架的转速。

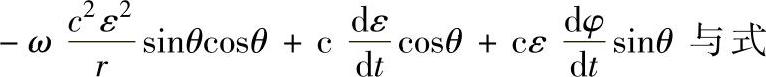
（6-90）右端括号内的多项式也是同一数量级，且括号前系数的数量级相同，因而也可以忽略不计，式（6-89）变成

设油膜在θ=0°～180°区域内产生动压，一般情况下，0°≤φ≤90°，当90°≤φ+θ≤180°+φ时，cos（φ+θ）为负，式（6-93）也为负值，该项建立的油膜压力为正值。因为当时，轴承表面的切向速度沿x方向变小，由于润滑油粘性的作用，出现润滑油的速度也有变小的趋势，导致润滑油出现淤积的趋势，从而产生正的油压。

3）考察式（6-91），其中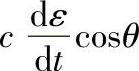、为行星轮系因制造和安装误差而引起的轴承中心相对于行星轮中心的运动速度，它们的位移代表了共转轴承对行星轮不均载的补偿量，即

ω=ω₂-ω_H

由于2K-H（NGW）型行星轮系的ω₂与ω_H方向相反，所以

|ω|=|ω₂|+|ω_H|

ω_H为行星轮轴的转速，也是行星轮与轴套所形成的共转轴承最小油膜厚度位置绕行星轮中心转动的速度。ω_H对挤压的影响如图6-42所示。当行星轮2和轴套1都以相同速度ω₂逆时针转动，而最小油膜厚度位置相对于固定的竖直线φ=0线以ω_H顺时针方向转动时，轴承两表面上的对应点M₁、M₂接近最小油膜厚度位置的速度为|ω|=|ω₂|+|ω_H|。所以，对于行星轮系中行星轮与轴套所形成的共转轴承来说，其最小油膜厚度位置随行星轮轴以ω_H转速变化，对油膜动压挤压项的作用相当于将轴承的速度提高了ω_H，这样轴承两表面法向接近的速度增大，使油膜的挤压作用得到加强。

将式（6-91）、式（6-92）、式（6-93）代入雷诺方程式（6-85），得到

解雷诺方程（6-94），得油膜压力p：(www.xing528.com)

首先对θ积分一次，其中h=c（1+εcosθ），得

当θ=θ₀或h=h₀时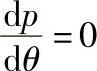，，可求得A，即

由方程（6-95），得

几个积分项的公式为

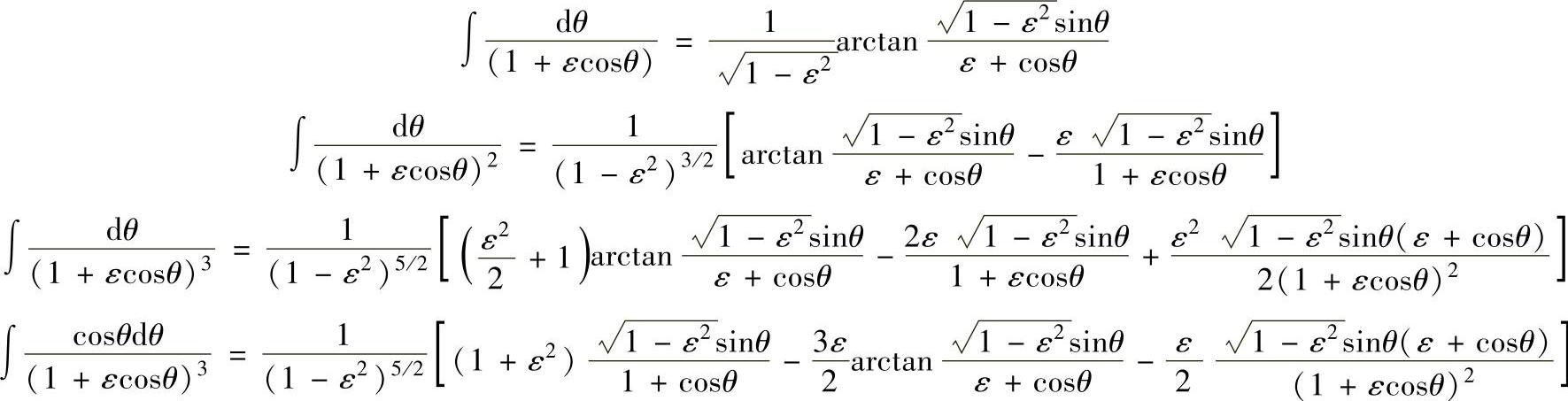
将式（6-96）积分得

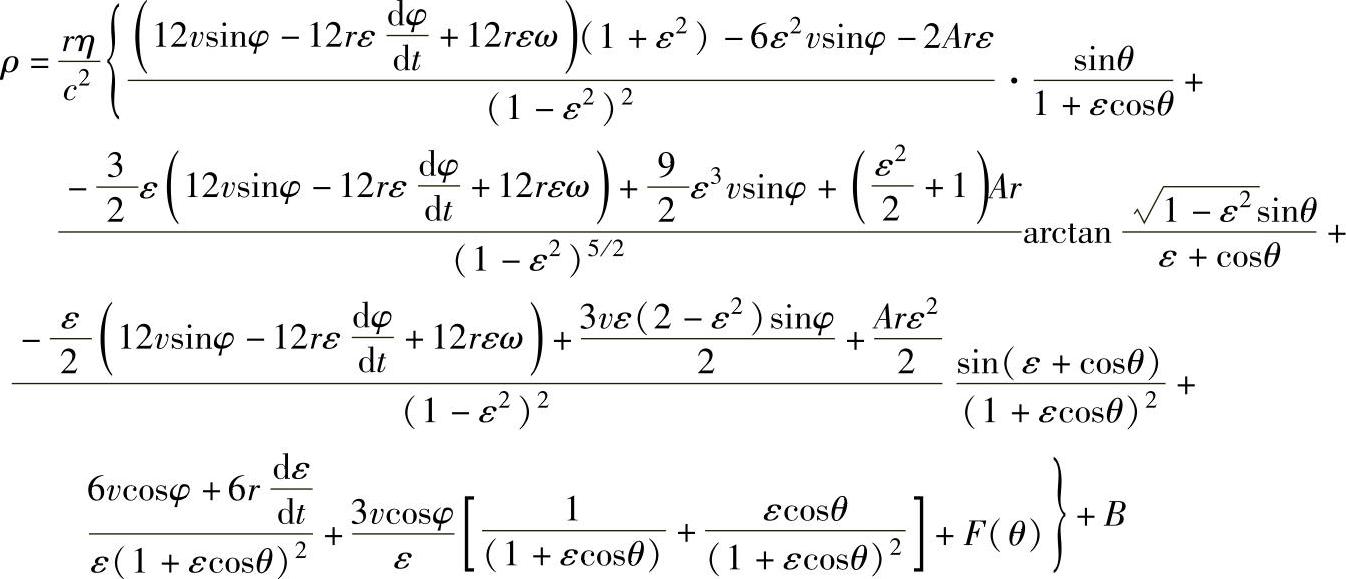
其中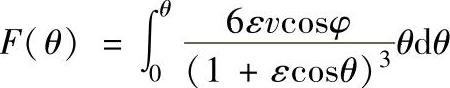，可用数值积分的方法求解。边界条件p（0）=p（2π）=p_a，可求出B。

p_a为油膜入口处的压力（θ=0时），θ₀为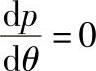时，对应的轴承位置。

系数·

系数

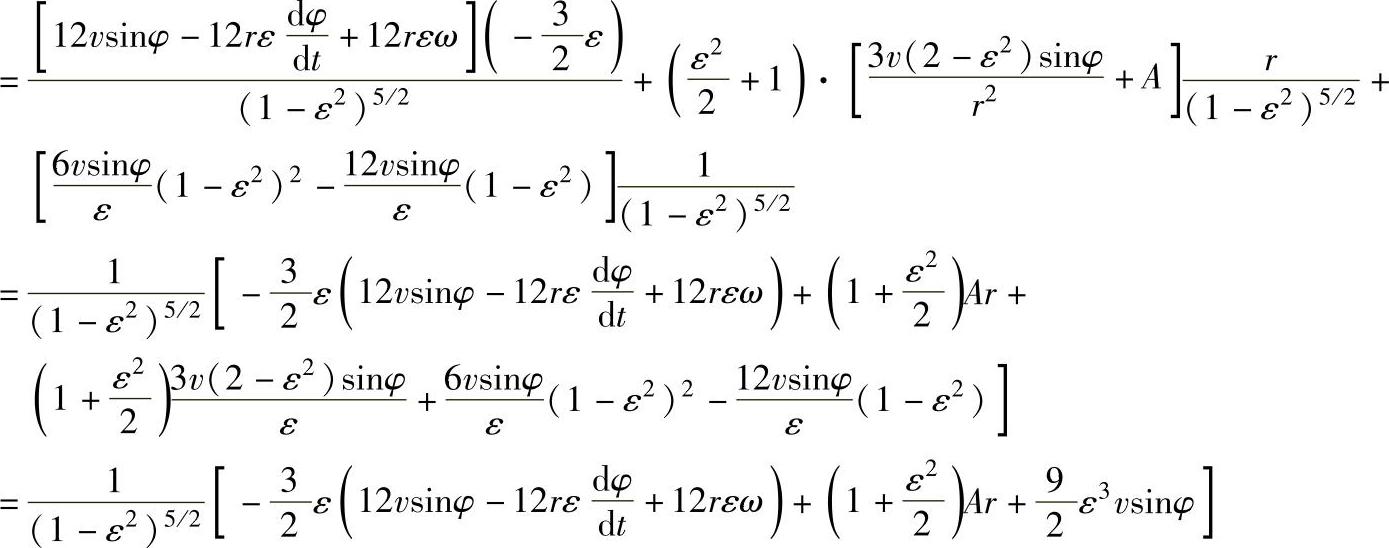
系数

（3）共转轴承油膜压力 从雷诺方程的求解过程，可以知道：

1）共转轴承的轴套外表面和行星轮内孔表面在每一对应的θ角位置上速度近似相等。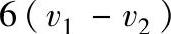，从而可忽略油楔项的影响。

2）由于行星轮中心存在线速度，因而轴承的同一表面上不同位置的切向速度不相同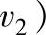，项不等于零。该项对油膜动压起增强的作用。

3）行星轮系共转轴承的最小油膜厚度位置，以速度ω_H绕行星轮中心转动，对油膜压力的影响相当于最小油膜位置固定，而将轴承的转速提高ω_H。油膜位置的变化只对挤压项起作用。

4）由于行星轮系各运动元件制造和安装误差的影响，轴套中心相对于行星轮中心的位置随时间而变化，它只对油膜的挤压项起作用。

图6-45所示是在有油膜情况下，行星轮中心随负载变化的轨迹（减速工作状态，不计及离心力），图中F_m为轴承单位面积上的平均载荷，Q为最小油膜厚度点，Q′为载荷作用点，φ为偏心角，O和O′分别为中间浮环和行星轮中心。当F_m增加时，偏心角由φ减小至φ′，Q点接近于Q′，O′移向O″，也就是当负载增加时，行星轮中心O′在负载作用线上从F′移至F″。这里用C_t表示油膜的弹性特性，则

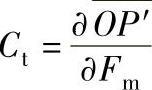
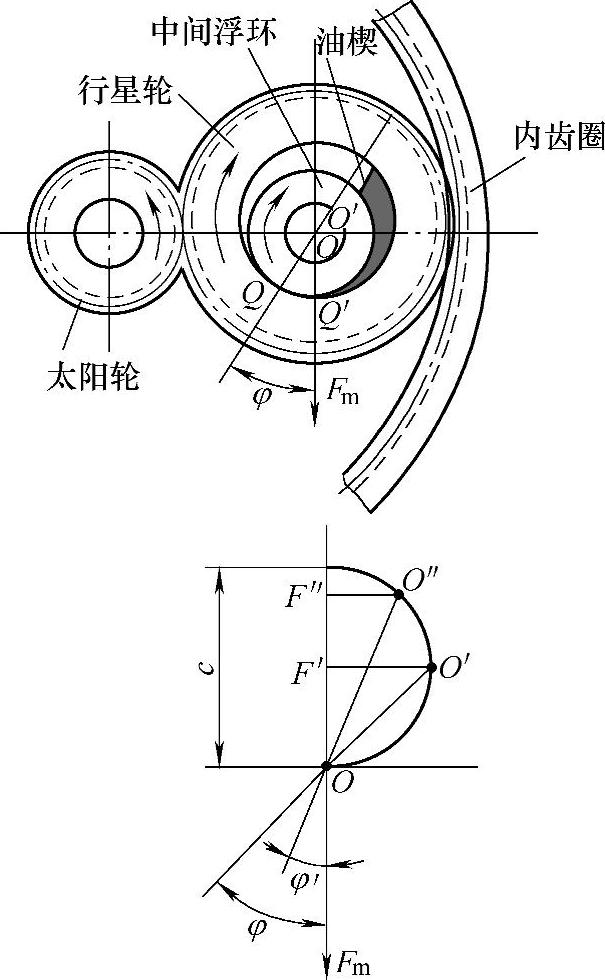
图6-45 行星轮中心随负载变化的轨迹

根据无限宽轴承理论

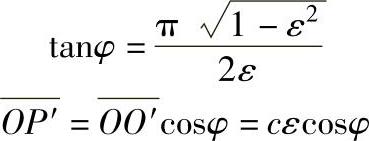
而且F_m也可表示为ε的函数，即

则

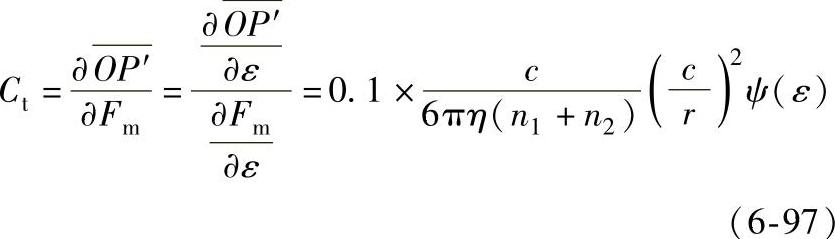
式中 ε——偏心率；

r——中间浮环半径（mm）；

η——润滑油动力粘度（MPa·s）；

n₁、n₂——行星轮和中间浮环转速（r/min）；

c——半径间隙（mm）；

ψ（ε）——偏心率ε的函数。

式（6-97）表示，当c增大时，C_t随之增大，C_t值越大对均载越有利，所以产生油膜的范围内希望取大的间隙值。

对于普通轴承，轴瓦和轴之一是固定的，如图6-46a所示，其轴承特性系数为

而对于具有中间浮环的情况下，如图6-46b所示，且当n₁=n₂时，则

式（6-98）和式（6-99）中，l₀、l为轴承宽度，c₀、c为轴承半径间隙，F为轴承的总负荷。若图6-46两种轴承的载荷相等，则特性系数也相等，即S=S′。当l₀=l时可得

从式（6-100）可见，当r≥r₀时，中间浮环和行星轮之间的间隙可以等于或大于普通滑动轴承的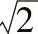倍。虽然图6-39c中的油膜均载效果更大，因为行星轮内孔和行星轮心轴之间存在着两种间隙和两层油膜。

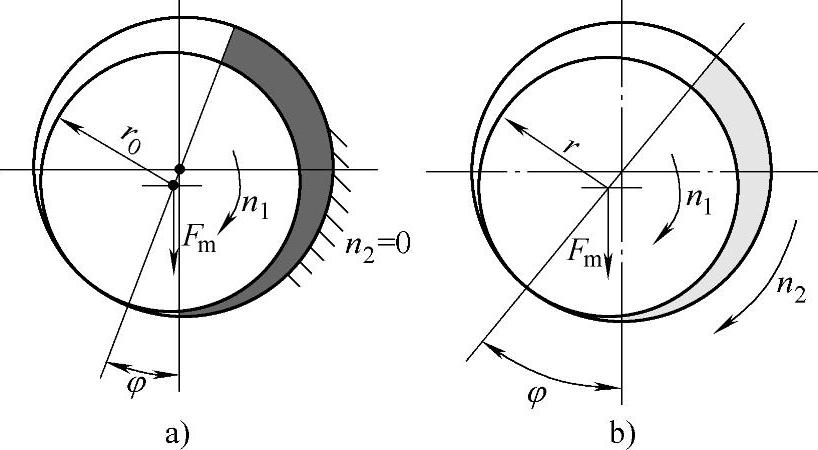
图6-46 两种形式的滑动轴承

设计时，间隙c与半径之比值，即相对间隙，推荐取0.0015～0.0045。当速度较高、直径较小时取大值，反之取较小值。中间浮环的宽度按齿轮宽度确定，而直径（亦即行星轮孔径）应在保证行星轮轮缘的情况下取较大值。因为直径越大，在轴承特性系数和负荷不变时可取较大间隙，以获得大的油膜柔性系数C_t。另外，还可以增加行星轮轮缘的柔性，以发挥其另一弹性均载作用。根据经验，一般取行星轮孔径与节圆直径之比为0.75～0.65，对于大模数取较小值，小模数取较大值。