常用的均载机构：基本构件浮动、弹性件、杠杆联动

（1）基本构件“浮动”的均载机构 基本构件“浮动”的均载机构是使太阳轮、内齿轮或行星架等基本构件在受力不平衡的条件下，能径向游动（浮动）。图6-21所示工作原理：当行星轮数n_p=3时，经过一个或两个基本构件浮动，可使作用在三个基本构件上的啮合力F_na、F_nb和2F各自形成力的封闭等边三角形。太阳轮a和内齿轮b的偏心量彼此相等，即e_a=e_b，其偏心方向的夹角等于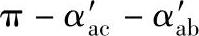（图6-21中未计弹性变形、惯性力和摩擦力的影响）。

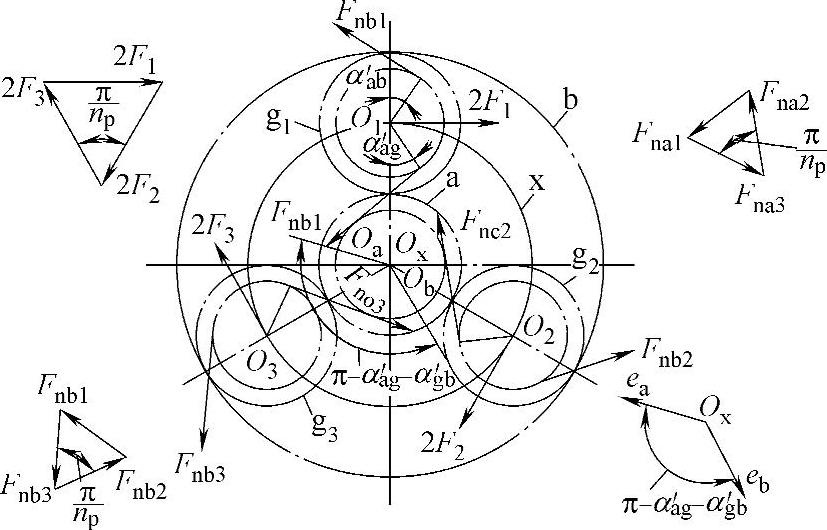
图6-21 当n_p=3时具有浮动件的NGW型传动理想受力状态

使基本构件浮动的最常用方法是采用双齿联轴器。三个基本构件中有一个浮动，即可起到均载作用，两个基本构件同时浮动时，效果更好。

1）太阳轮浮动。太阳轮通过双齿联轴器与高速轴相连接（见图6-22）。因为太阳轮重量较小，浮动灵敏，机构简单，容易制造，故应用广泛。当n_p=3中低速时，均载效果显著。当n_p＞3高速时，效果不好，噪声偏大。载荷不均匀系数K_p=1.1～1.15。

2）内齿圈浮动。内齿圈通过双齿联轴器与机体相连接。优点是结构的轴向尺寸较小，缺点是浮动件尺寸大、质量大、加工不方便，浮动灵敏性较差，均载效果不如太阳轮浮动好。

NGWN型行星传动，常采用内齿圈浮动（见图6-23）。

3）行星架浮动。行星架通过双齿联轴器与低速轴相连接。行星架浮动不要支承可简化结构，特别是简化多级行星传动，如图6-24所示。由于行星架质量较大，在速度较高和制造质量较差的情况下，离心力较大，影响浮动效果，所以在质量不大、速度不高的情况下，采用较合适。在齿轮制造精度为7级，其他零件不低于2级精度时，载荷不均匀系数K_p=1.2～1.3。

4）太阳轮和行星架同时浮动，此法比两者单独浮动效果要好，如图6-25所示。

5）太阳轮和内齿圈同时浮动。此法主要用于高速行星传动。优点：噪声小，浮动效果好，工作可靠。如图6-26所示，内齿圈通过两个齿套与箱体连接，太阳轮不装轴承，用长齿套连接动力源或工作机械。为了增加浮动效果，内齿圈应尽量减薄，以增加柔性。载荷不均匀系数K_p=1.1～1.15。

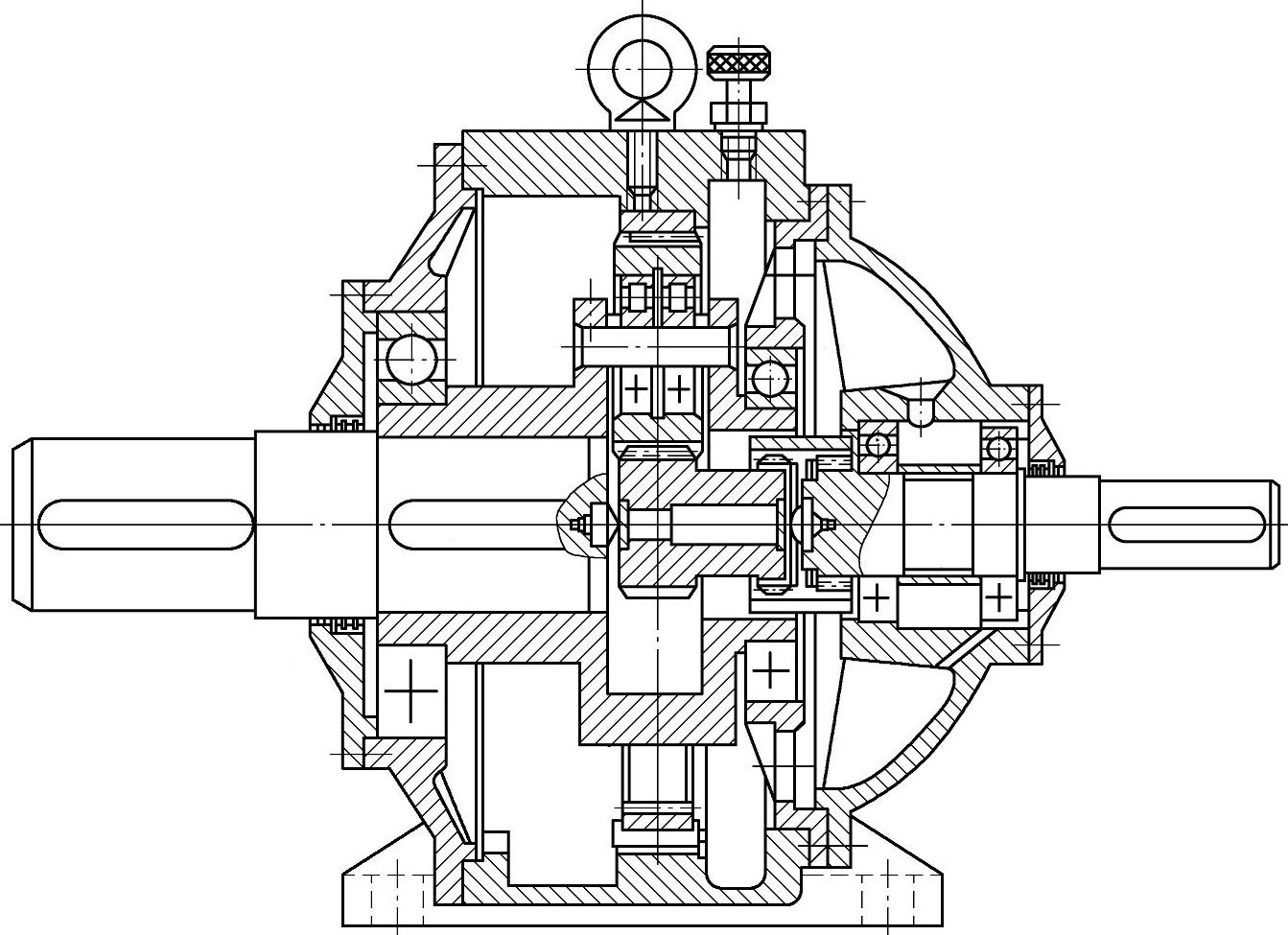
图6-22 单级2K-H（NGW）型太阳轮浮动

图6-23 3K（NGWN）型内齿轮浮动

6）无多余约束的浮动方法。图6-27所示是这种浮动机构的原理图。图6-28所示是这种浮动机构在双级行星传动中的应用。此法在行星轮中装置一个球面调心轴承。单级传动中，太阳轮利用单齿联轴器进行浮动。双级传动中，高速级行星架无支承并与低速级太阳轮固定连接。此法优点是机构中无多余约束，结构简单，浮动效果好，沿齿长方向的载荷分布均匀。由于行星轮内只装一个轴承，当传动比较小时，轴承尺寸小，寿命较短。

（2）采用弹性件的均载机构 这种机构主要通过弹性元件的弹性变形使各行星轮载荷均匀，常见形式有如下几种：

1）靠齿轮本身弹性变形的均载机构。如图6_-29所示，采用薄壁内齿轮，靠内齿轮的弹性变形达到均载目的。图6-26所示中，合理设计内齿轮结构，也具有弹性均载作用。图6-30所示是另一种高速行星传动的结构，同时采用了薄壁内齿轮。带有细长轴的太阳轮和中空轴支承的行星结构，尽量增加各基本元件的弹性。优点：零件数量少，外廓尺寸小，减振性好，行星轮数可大于3。缺点：制造精度要求高，悬臂长度、壁厚和柔性要设计合理，否则影响均载效果，产生沿齿长的载荷集中。

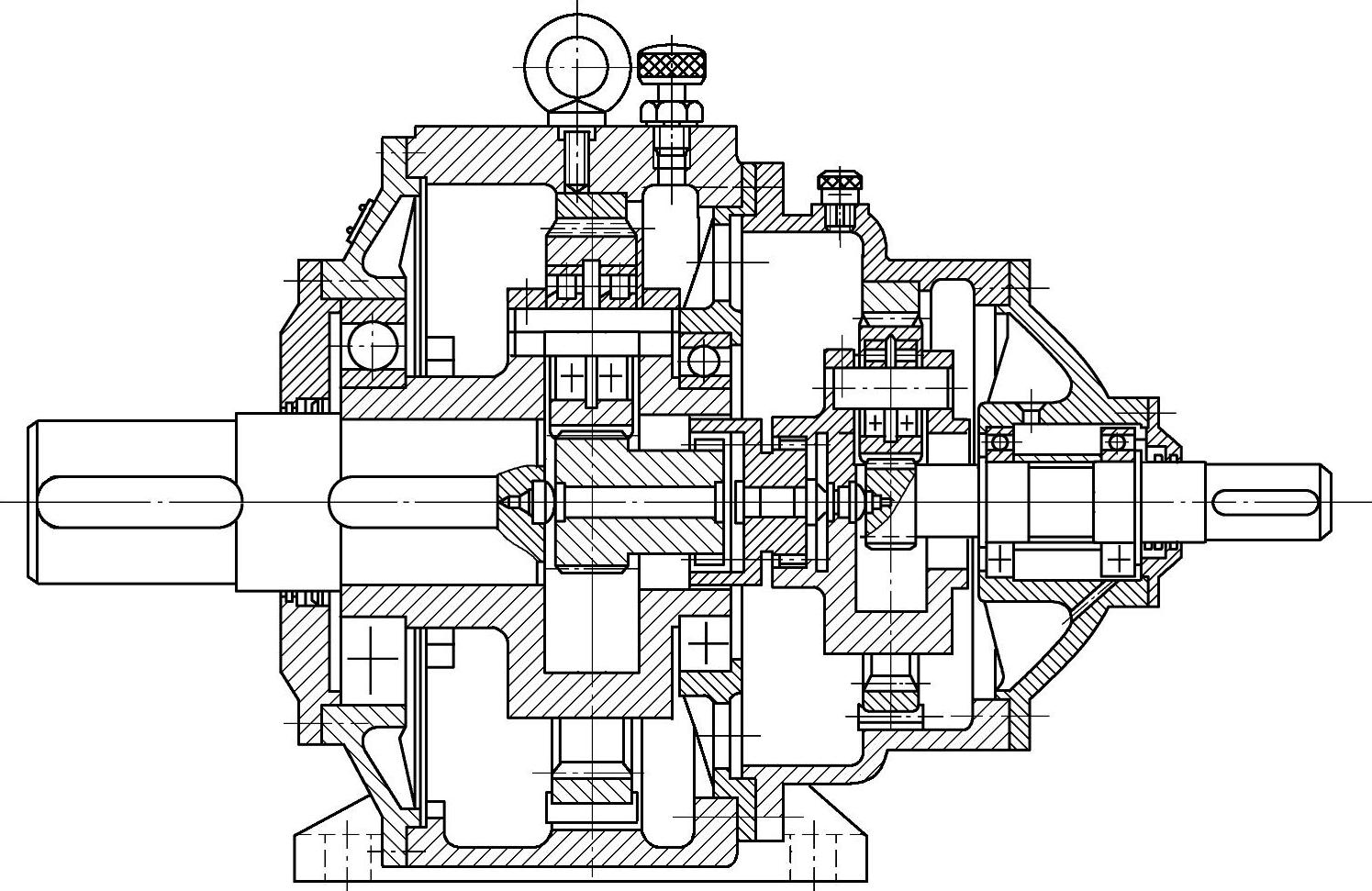
图6-24 双级2K-H（NGW）型减速器（高速行星架浮动，低速太阳轮浮动）

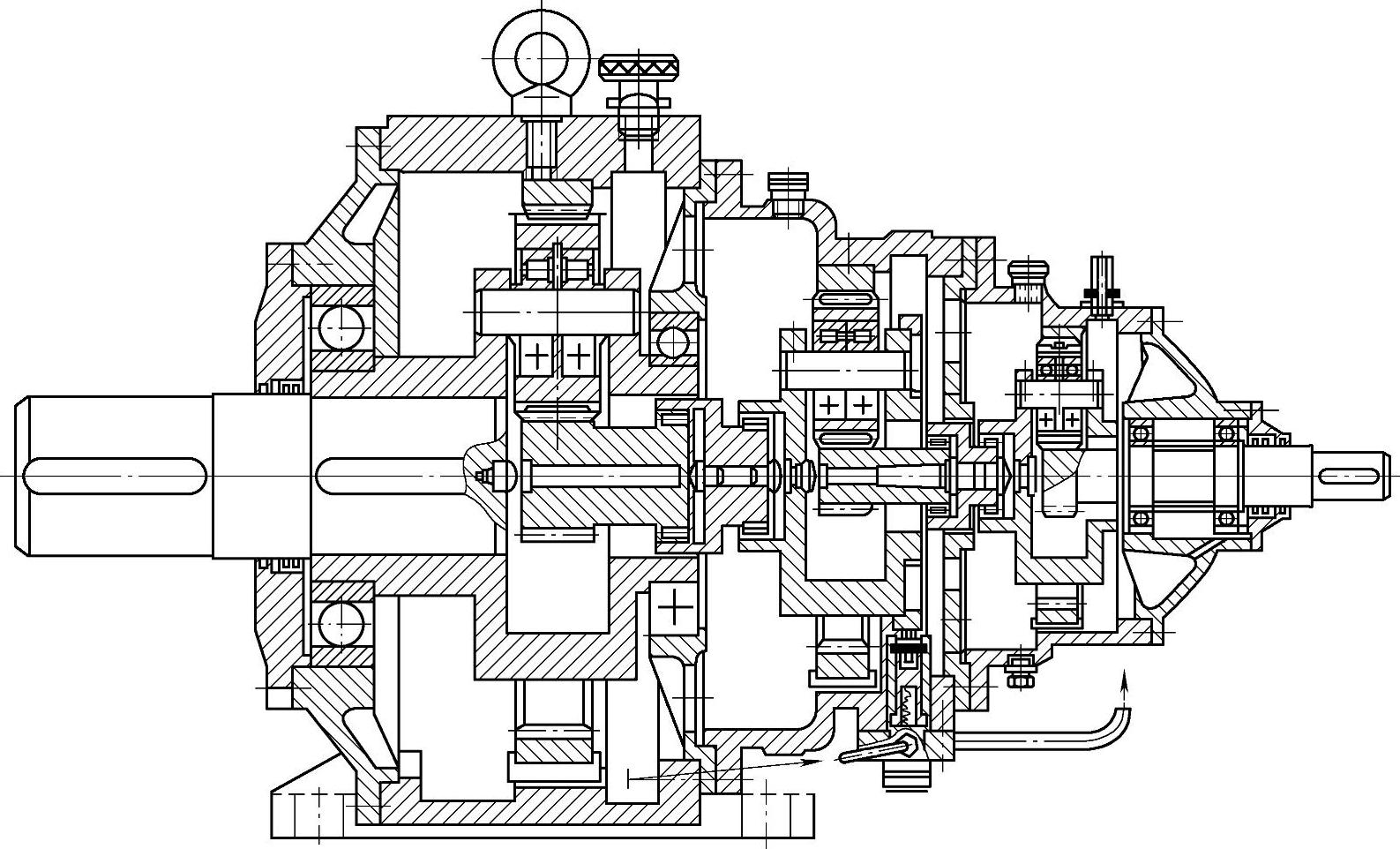
图6-25 三级2K-H（NGW）型减速器（中间级太阳轮和行星架同时浮动）

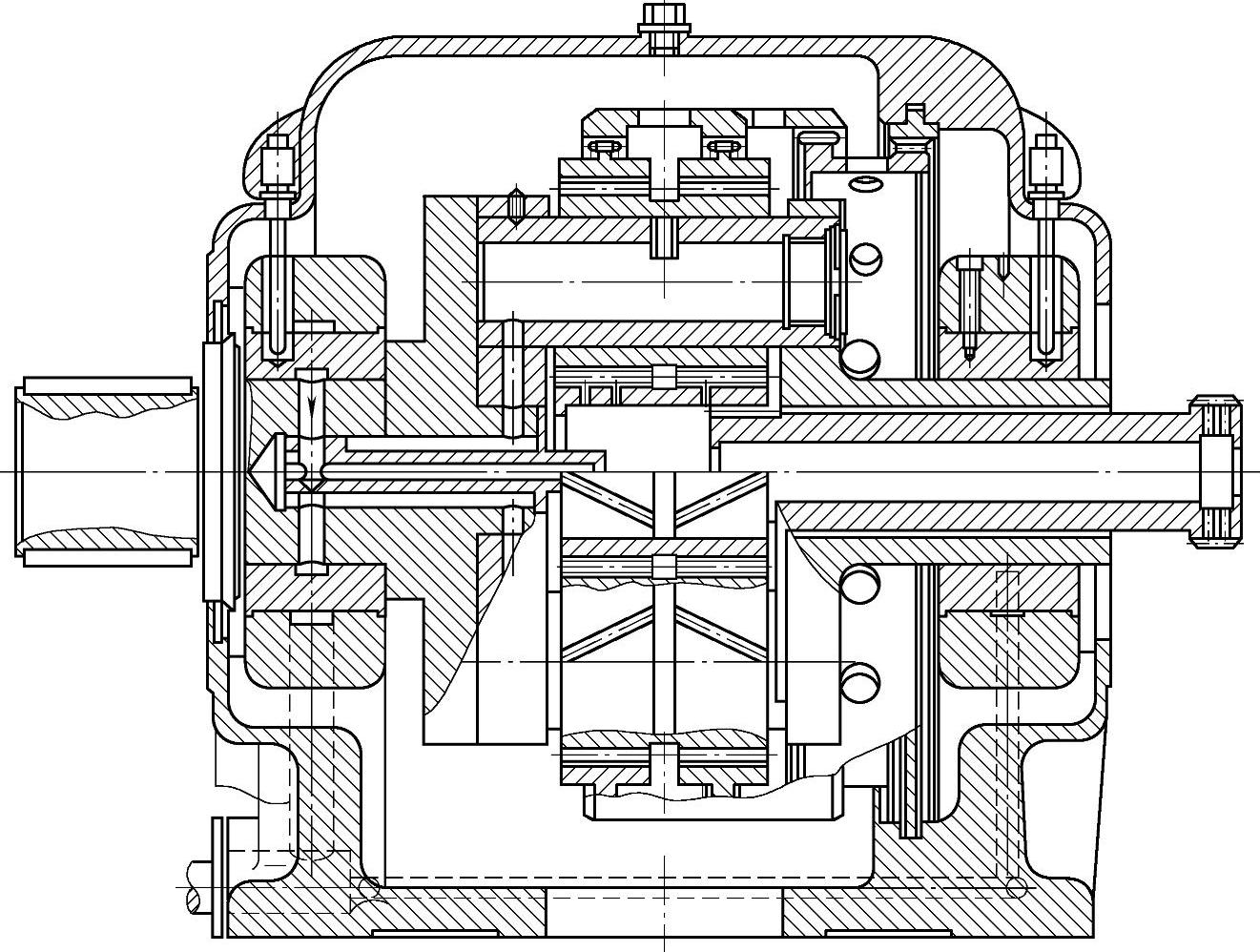
图6-26 2K-H型太阳轮和内齿轮浮动的高速行星传动（n_p=4）

2）采用弹性销的方法。如图6-31所示，内齿轮通过弹性销与机体固定，弹性销由多层弹簧圈组成。如图6-32所示（图中机体未示出，太阳轮靠双齿联轴器浮动），弹性销在长度方向分成五段装在一起，这种结构径向尺寸小，有较好的缓冲减振性能。

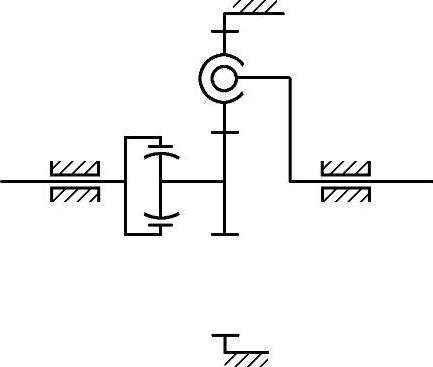
图6-27 无多余约束的浮动机构

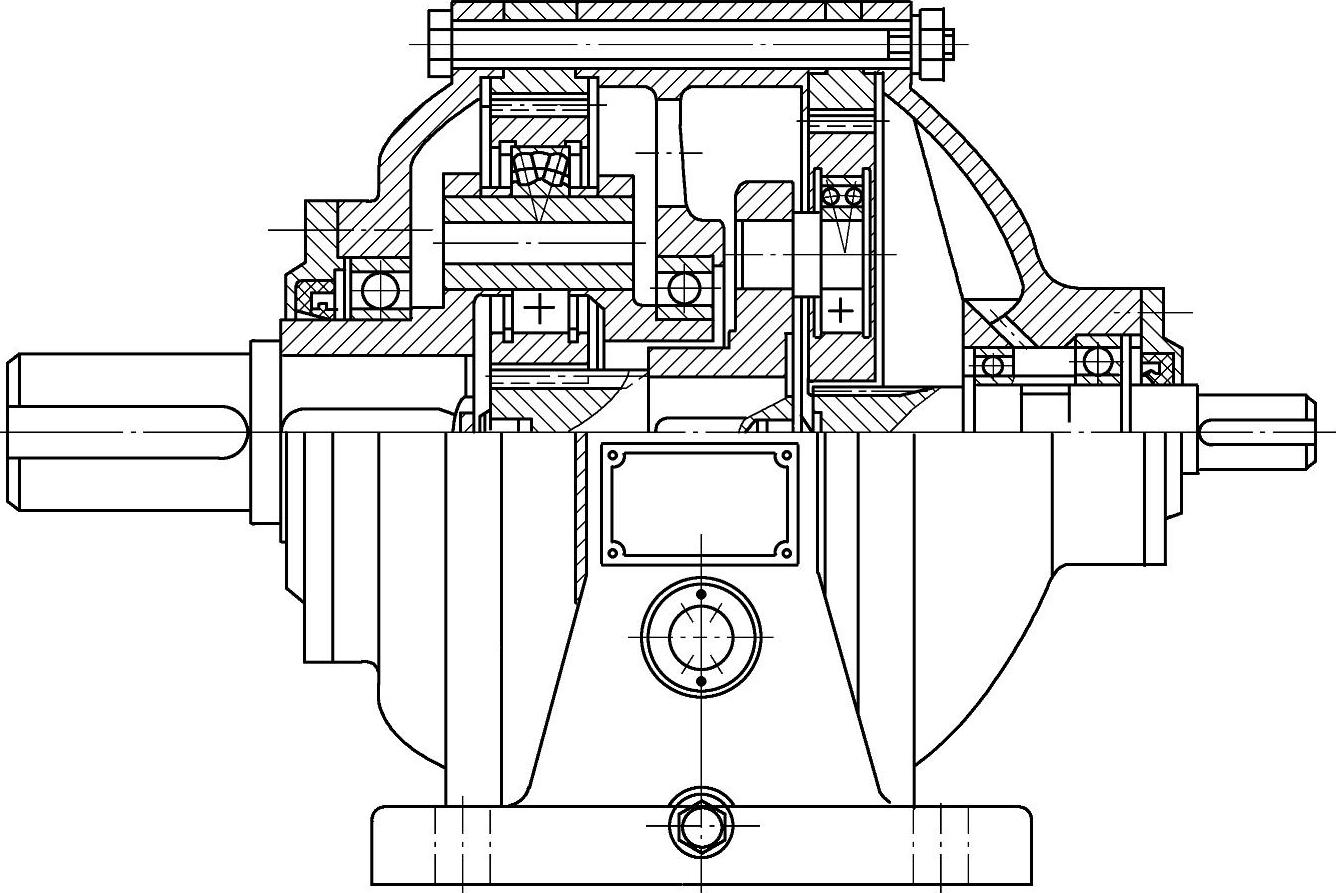
图6-28 无多余约束的双级减速器

3）用弹性件支承行星轮。在行星轮孔与行星轮轴之间或行星轴与行星架之间（见图6-33）安装非金属（如尼龙类）的弹性衬套。此法结构较简单，缓冲性能好，行星轮数可大于3。但非金属弹性套有老化和热膨胀等缺点，工作温度不能过高，不能用于啮合角α_a′_g＞α_g′_b的角变位传动。

弹性件均载机构缺点：这类机构都依靠各弹性件弹性变形补偿误差，各件变形程度不同，影响载荷分布，弹性件刚度越大，制造误差越大，则载荷不均匀系数越大。

（3）杠杆联动均载机构 杠杆联动均载机构中装有带偏心的行星轮轴和连杆。

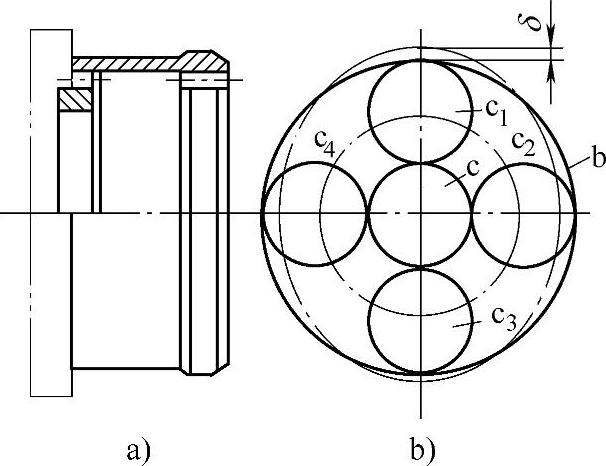
图6-29 薄壁内齿轮

a）安装形式 b）变形形式

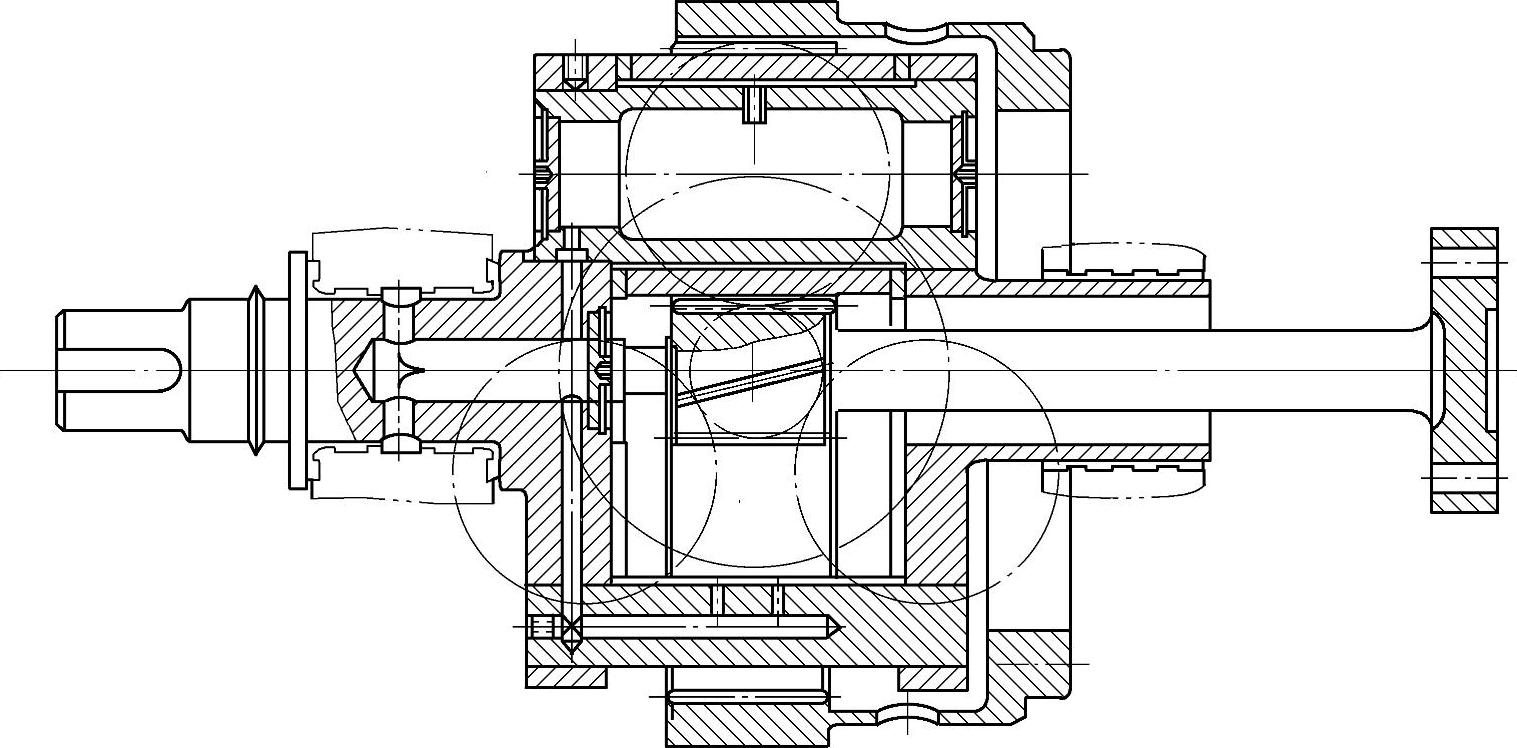
图6-30 靠柔性均载的高速行星机构（斜齿轮）(https://www.xing528.com)

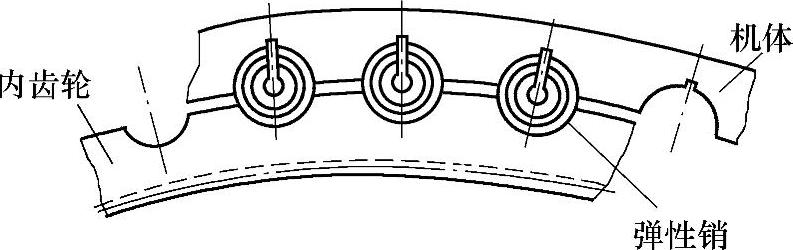
图6-31 弹性销结构

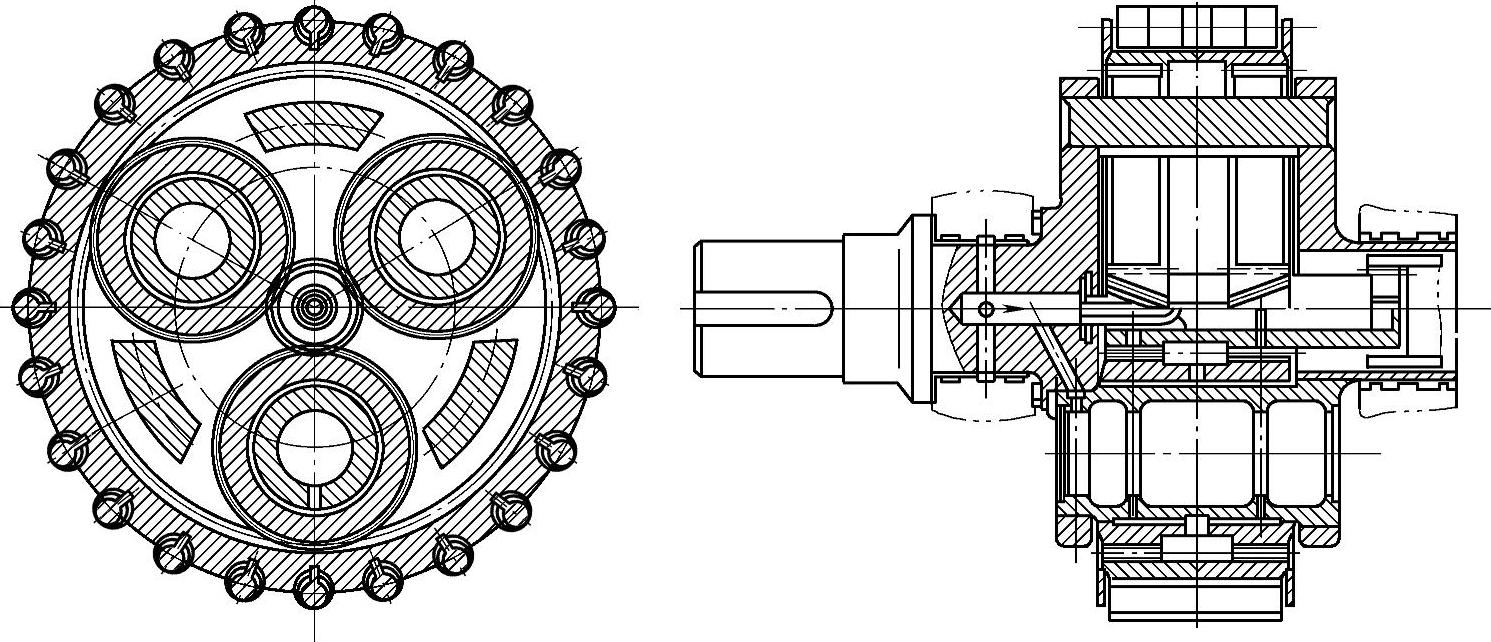
图6-32 内齿轮用弹性销固定的高速行星传动

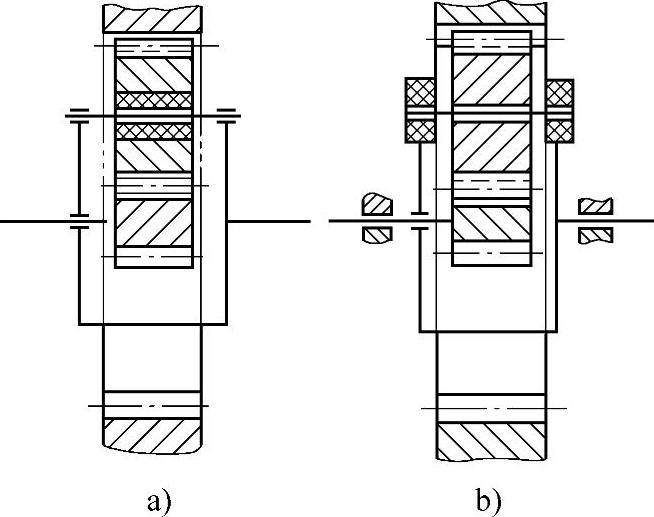
图6-33 行星轮弹性支承

a）行星轮轴孔中安装弹性衬套 b）行星架轴孔中安装弹性衬套

1）两行星轮联动机构。如图6-34所示，行星轮对称安装，在两个行星轮偏心轴上分别固定一对互相啮合的扇形齿轮（相当于连杆），当一个偏心轴回转时，由于齿扇啮合的杠杆作用，另一个偏心轴作相等而方向相反的回转，两行星轮的载荷达到均衡。扇形齿轮上的圆周力

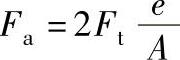
式中 e——偏心距，可取；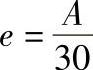

F_t——齿轮圆周力。

载荷不均匀系数K_p=1.05～1.1。

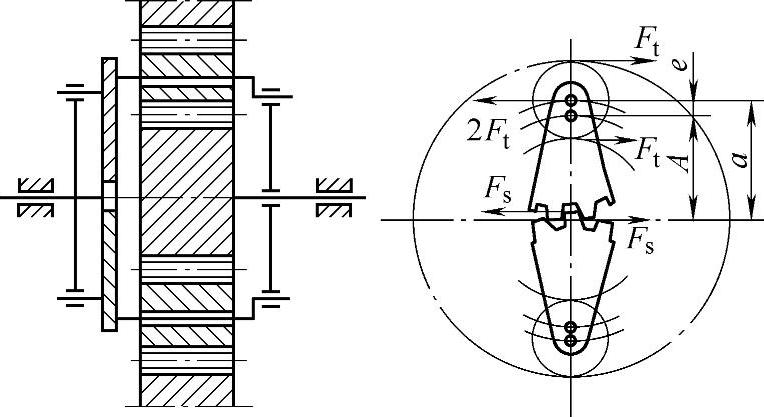
图6-34 两行星轮联动机构

2）三行星轮联动机构。图6-35所示为三行星轮的NGW型结构，平衡杆的一端与行星轮偏心轴固接，另一端与浮动环活动连接，六个啮合点所受的力大小相等时，机构才能过到平衡。当载荷不均衡时，作用在浮动环上的三个径向力F_s不等，浮动环产生移动或转动，直至三力平衡为止。

图中浮动环中心圆半径r=0.5A，A=a-e，平衡杠杆长度ρ=Acos30°，一般取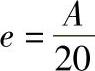，作用于浮动环的力F_s按下式计算

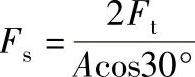
载荷不均匀系数K_p=1.1～1.15。

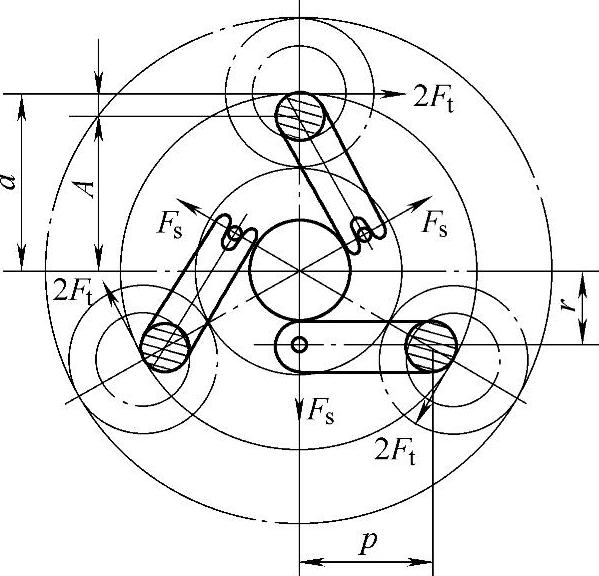
图6-35 三行星轮联动机构

3）四行星轮联动机构。图6-36a、b所示为四行星轮联动机构。

图6-36中根据平衡条件，构件尺寸应满足r₁∶s₁=r₂∶s₂的关系。取r₁≈r₂=14e，e=a/20～a/30，载荷不均匀系数K_p=1.1～1.15。

杠杆联动均载机构的均载效果较好，但结构较复杂。为了提高灵敏度，偏心轴用滚针轴承支承，使整个传动的轴承数量增多，小传动比时，行星轮轴承寿命较短，这种均载机构适用于中、低速传动。

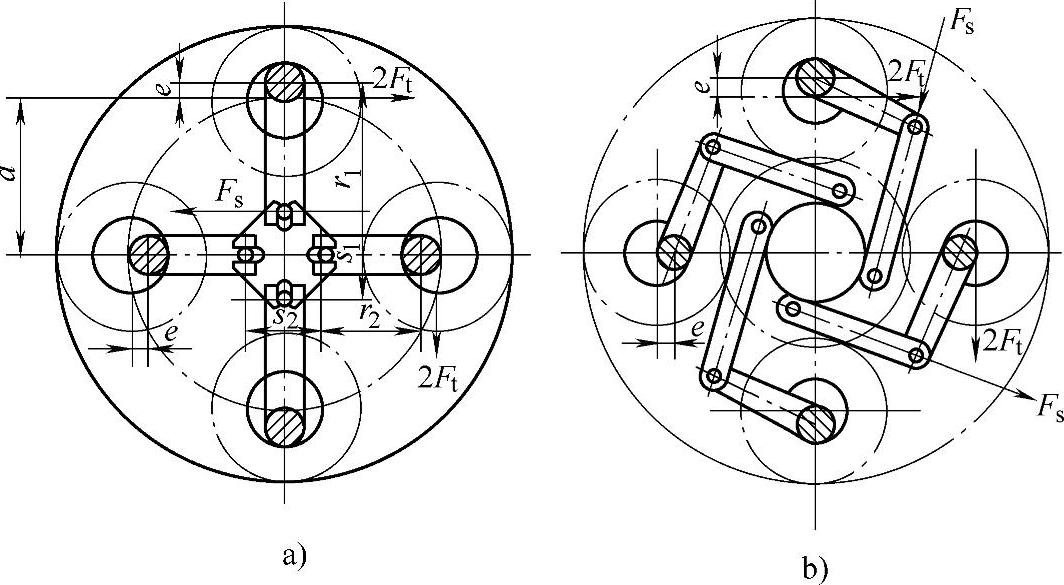
图6-36 四行星轮联动机构

双齿联轴器的内齿套长度（见图6-37）：

式中 E_max——浮动件的最大浮动量；

ω——联轴器内齿套允许最大歪斜角度，一般为30′，对鼓形齿联轴器可取1°左右。

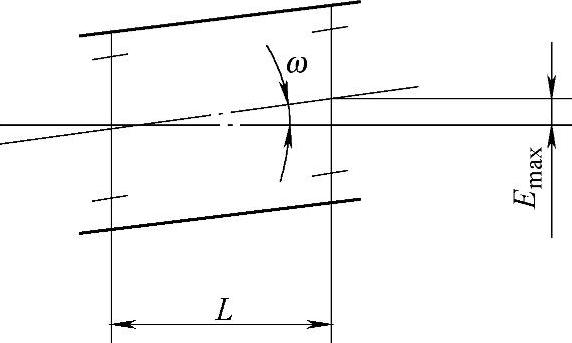
图6-37 内齿套长度的确定

（4）浮动用齿轮联轴器

1）主要参数推荐。齿形为渐开线直齿；压力角为α=20°；齿顶高系数h_a∗=0.8；齿宽b≤1/3d；齿数：为了避免内齿轮产生径向切入顶切，应根据插齿刀的参数，选择变位系数和最小齿数。

2）强度验算。主要验算轮齿的挤压应力。