行星差动轮系有两种应用方式,其一是用于合成运动,作为变速器使用;其二是用于运动分解,作为行星差动使用,现就这两种情况进行运动学分析。
(1)用行星差动轮系合成运动时的转速计算 设周转轮系的三个基本构件分别为A、B、C,并以转速nA、nB、nC旋转,根据相对运动原理,按件A固定,可得
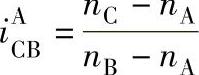
或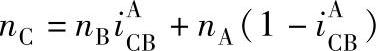
由普遍关系式知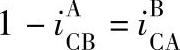 ,可将上式化为
,可将上式化为
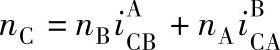
同理,分别按件B、C固定,可得到关于nA及nB的表达式。将这三个表达式用三个基本构件为a、b、H的2K-H型轮系表示
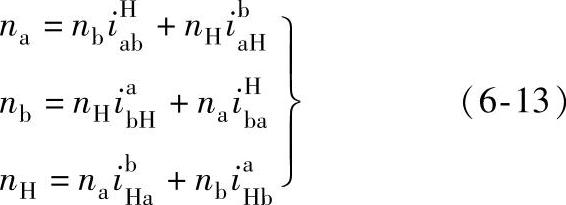
式(6-13)是根据行星差动轮系两个主动构件的转速求从动构件转速的普遍关系式。其等号左边为从动构件的转速,右边两项分别为一个主动构件旋转与另一主动构件固定时,从动构件对主动构件传动比的乘积。并且,如果分析式(6-13)中第一式的右边,并注意到主动构件的转速与轮系中固定构件的确定无关,其中第一项
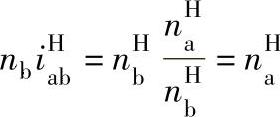
第二项
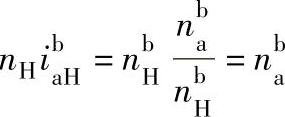
则此式变为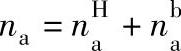
因此,式(6-13)变为
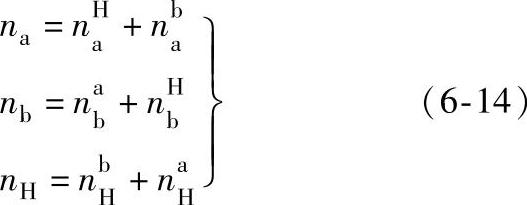
上式说明行星差动轮系合成运动时,从动构件的转速由两个主动构件分别固定时,机构按行星轮系传动时从动构件转速的代数和确定。
行星差动轮系一般都采用2K-H型轮系,常用的有NGW型(见图6-3)、WW型(见图6-4)和ZUWGW型(见图6-5)。由于三个基本构件的轴线均重合于主轴线,差动运转时从动构件的转速可用式(6-13)和式(6-14)计算。
例6-5 50t氧气顶吹转炉倾动机构中,采用了NGW型行星差动轮系,以达到变速的目的。图6-3所示为该传动系统机构简图。试根据已知数据计算主、辅电动机M和行星差动轮系配合能使转炉得到的四种倾动转速。
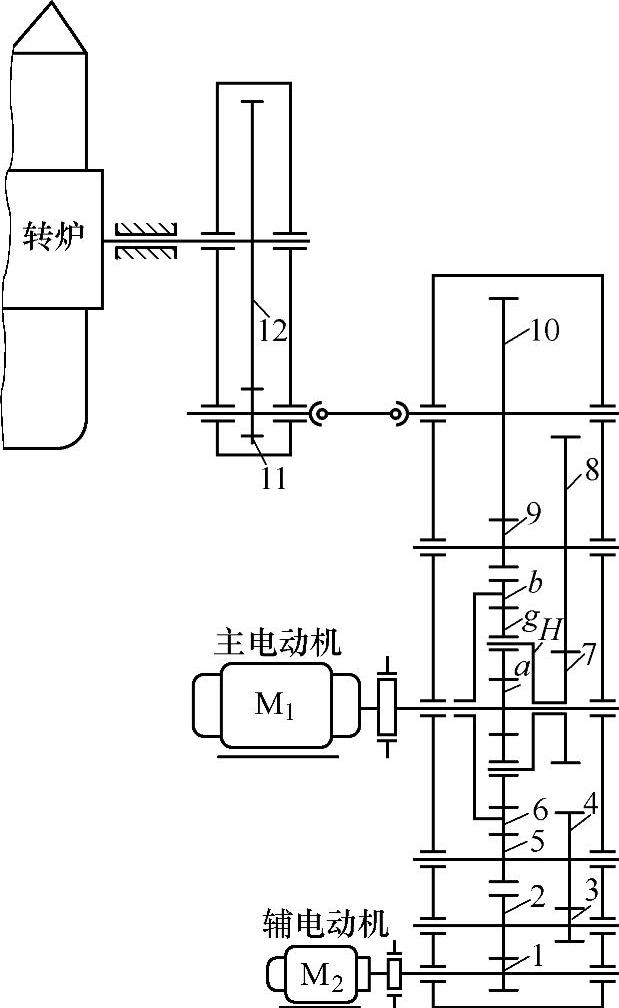
图6-3 转炉倾动机构行星差动传动系统机构简图
已知z1=20,z2=92,z3=23,z4=100,z5=28,z6=104,za=24,zg=39,zb=104;z7=29,z8=95,z9=21,z10=95,z11=20,z12=146。电动机M1的功率P1=125kW,转速na=580r/min。电动机M2的功率P2=13kW,转速n1=975r/min。
解 传动系统可分为齿轮1~6组成的定轴轮系Ⅱ,齿轮7~12组成的定轴轮系Ⅰ,以及中心轮a、b和转臂H、行星轮g组成的NGW型行星差动轮系三部分。iⅡ=-74.3,iⅠ=-108.2,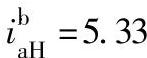 ,
,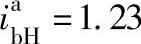 。
。
1)主电动机M1运转,辅电动机M2停转,即na=580r/min,nb=0时,得第一种倾动转速nⅠ。

而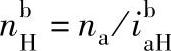 ,故
,故
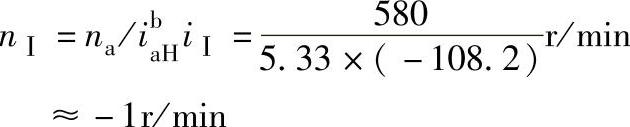
转炉倾动方向与主电动机M1转向相反。
2)主电动机M1停转,辅电动机M2运转,即na=0,nb=nⅠ/iⅡ=975/(-74.3)r/min=-13.1r/min,转炉得第二种倾动转速nⅡ
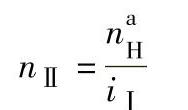
而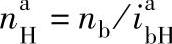 ,故
,故
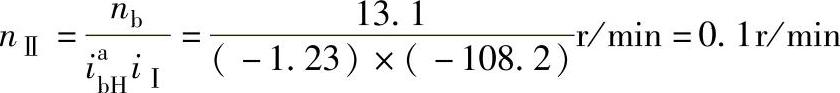
转炉倾动方向与电动机M2转向相同。
3)电动机M1、M2都运转,并且轮a与轮b转向相同时,得第三种倾动转速nⅢ根据式(6-14),转臂转速为
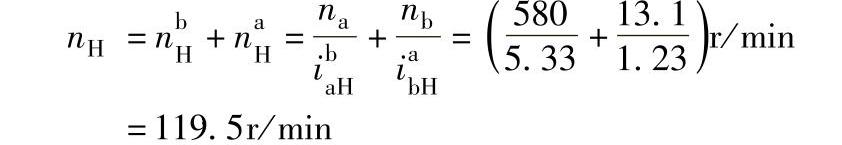
nⅢ=nH/iⅠ=119.5/(-108.2)r/min=-1.1r/min
转炉倾动方向与轮a和b的转向相反。
4)主、辅电动机M1和M2都运转,但轮a与轮b转向相反时,得第四种倾动转速nⅣ。
设以轮a的转向为正,轮b转向为负,则转臂H的转速为
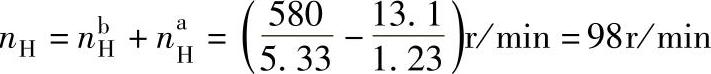 (https://www.xing528.com)
(https://www.xing528.com)
nⅣ=nH/iⅠ=98/(-108.2)r/min=-0.9r/min
转炉倾动方向与轮a转向相反。
计算结果表明,主、辅电动机与行星差动轮系配合,可使转炉向每个方向都得到四种倾动转速。计算中的“+”、“-”号表示主、从动构件的转向关系。
例6-6 图6-4所示为小型冷连轧机改造中增设一个有2K-H(WW)型行星差动轮系的减速系统机构简图。试根据已知数据计算从动轴的四种转速。
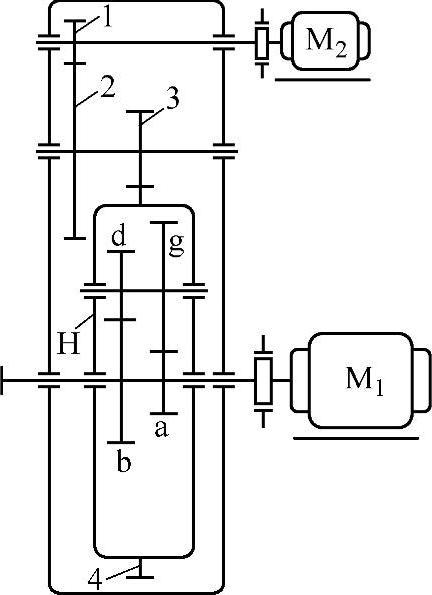
图6-4 小型冷连轧机的WW型行星差动机构简图
已知z1=22,z2=77,z3=34,z4=166,i14=(z2z4)/(z1z3)=17.1;za=26,zg=43,zb=43,zd=26。电动机M1的功率P1=20kW,转速na=950r/min。电动机M2的功率P2=3kW,转速n1=1000r/min。
解 1)主电动机M1运转,辅电动机M2停转,即na=950r/min,nH=0时得第一种转速nbⅠ,行星差动轮系变为定轴轮系
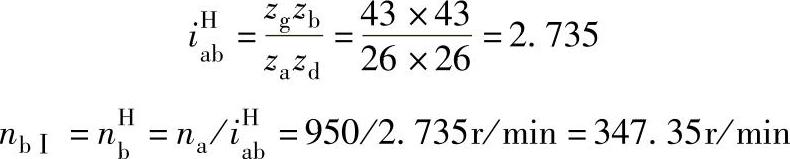
输出齿轮b与电动机M1的转向相同。
2)主电动机M1停转,辅电动机M2运转,即na=0,nH=n1/i14=1000/17.1r/min=58.5r/min,此时行星差动轮系变为轮a固定、H主动、轮b从动的行星轮系,得第二种转速nbⅡ,即

输出齿轮b与电动机M2的转向相同。
3)主电动机M1和辅电动机M2都运转,而且使na与nH转向相同。此时轮系为行星差动轮系,按式(6-14)得从动构件的第三种转速nbⅢ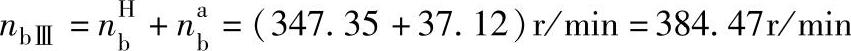
输出齿轮b转向与na、nH相同。
4)主电动机M1和辅电动机M2都运转,但使na与nH转向相反。此时仍为行星差动轮系,按式(6-14)得从动构件的第四种转速nbⅣ。
若以na为正,则nH=-58.5r/min,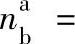
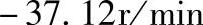 ,
,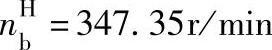 ,于是
,于是
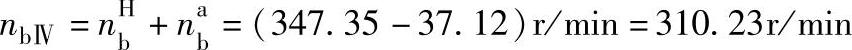
输出齿轮b的转向与na相同。
计算结果是,从动构件能得到与主动构件相同转向的四种转速:37.12r/min、310.23r/min、347.35r/min、384.47r/min。
当辅助电动机采用直流电动机调速时,从动构件可得到在几个范围内的无级调速。
(2)用行星差动轮系分解运动时的转速计算 行星差动轮系的一个基本构件主动时,其输入运动可按任何比例,分解给另外两个基本构件输出。分解比例可按需要给定,也可受传动系统性能的影响,随机地变化。下面以汽车后桥的差速器为例说明。
例6-7 图6-5所示为汽车后桥行星差动系统及转向示意图。输入轴转速为n1,试求汽车直前行驶和以半径R转弯行驶时两后轮的转速na、nb。

图6-5 汽车后桥差动系统及转向示意图
解 汽车发动机的转速经变速器减速后,以转速n1传给行星差速器输入轴齿轮1。行星差速器由齿轮1、2组成的定轴轮系,和由中心轮a和b、行星轮g、转臂H组成的ZU-WGW型行星差动轮系构成。n1经定轴轮系输入行星传动轮系,然后按汽车转向时的几何关系和运动关系分解。
应用转臂固定法得转速关系方程式
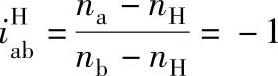
即
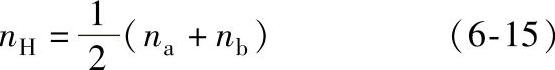
当汽车直前行驶时,在同一时间间隔内,左、右两车轮滚过路程应相等。因两轮外径相等,其转速也应相等,即na=nb。因此,行星轮g没有自转运动,两个中心轮a、b和行星轮g如同一个构件,随同转臂H一起转动,其转速为
na=nb=nH=n1/i12
当汽车沿弯路行驶时,在同一时间间隔内左、右车轮滚过的路程不相等,其转速也不相等。设车轮半径为r,轮距为2l,汽车转弯的角速度为ω,车轮在路面上作纯滚动时必有
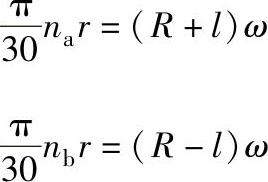
两式相除得两轮的转速比为

联立解式(6-15)和式(6-16)得两车轮的转速
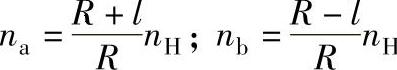
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




