计算1.2K-H（NGW）型行星轮系传动比的方法

（1）负号机构2K-H型行星轮系的传动比计算 单排2K-H（NGW）型行星轮系（见表6-5中序号1）和双联行星轮内外啮合2K-H（NW）型行星轮系（见表6-5中序号2）均为负号机构，其转化机构传动比均为负值。

2K-H（NGW）型，；2K-H（NW）型，

表6-5 用普遍关系式计算2K-H型行星轮系的传动比

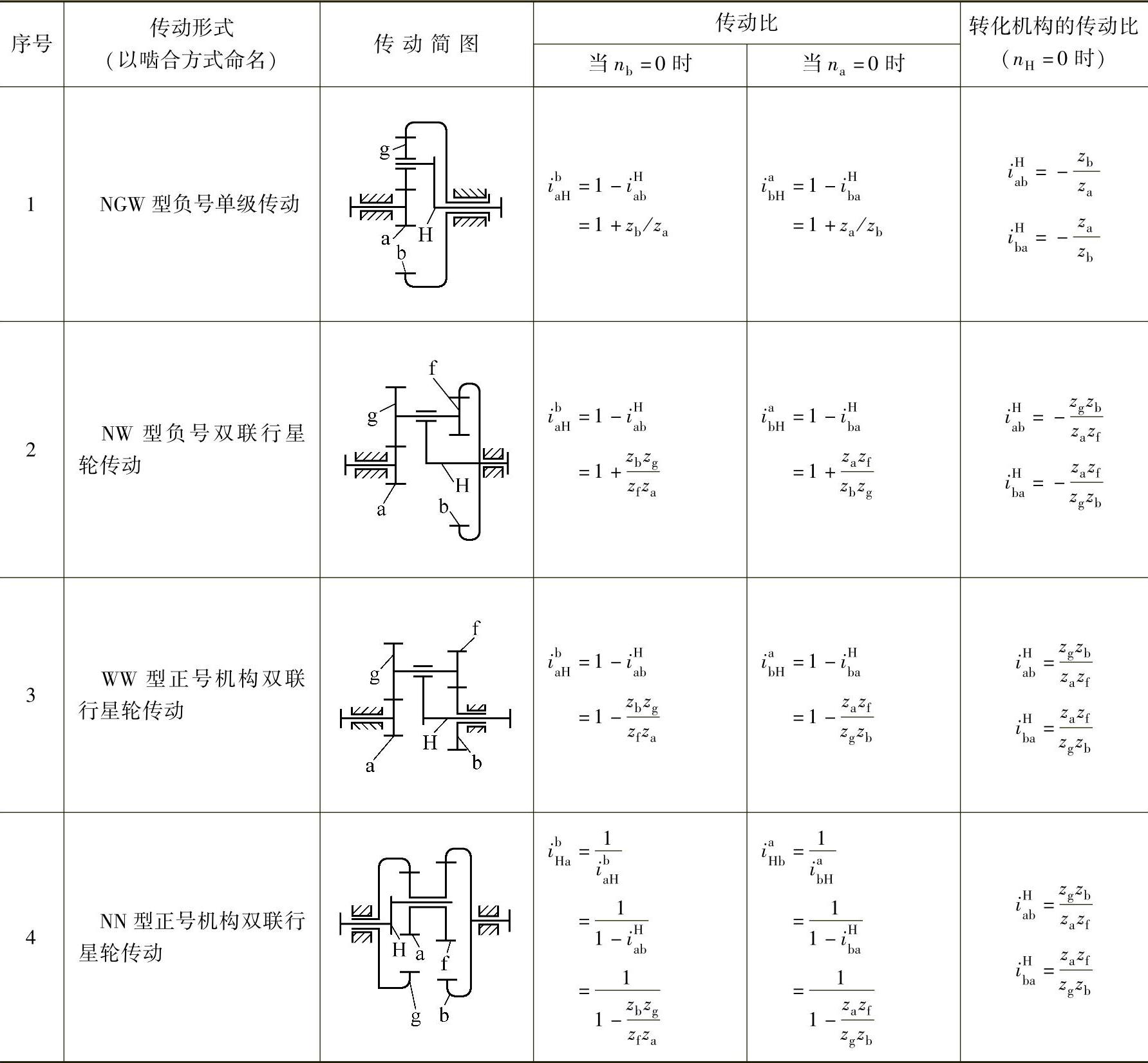
当求时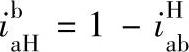，（应用普遍方程式），将转化机构传动比代入，得

2K-H（NGW）型

2K-H（NW）型

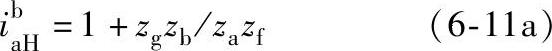
当求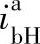时，同理可得

2K-H（NGW）型

2K-H（NW）型

当求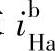时，所求的传动比i的第一个下标为行星架H，这时首先应该用“更换下标、互为倒数”，将第一个下标H换到第二个下标位置，然后再应用普遍方程式进一步列式。

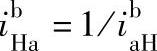（应用“更换下标、互为倒数”）=1/（应用普遍方程式）。

代入转化机构传动比得

2K-H（NGW）型

2K-H（NW）型

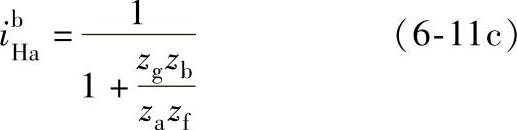
当求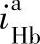时，同理可得2K-H（NGW）型

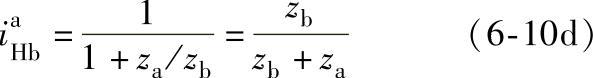
2K-H（NW）型

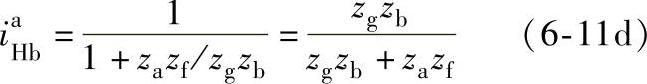
可见，不同的形式、不同的固定构件和主、从动构件，其传动比公式就不同。但是它们列式的方法都是一样的，就是应用普遍方程式和“更换下标、互为倒数”这两个既易记又简便的方法。

例6-1 在表6-5序号1中所示为单排2K-H（NGW）型行星轮系，已知z_a=24，z_g=36，z_b=96，试求、、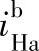和。

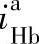解 1）转化机构传动比

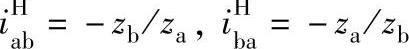
2）应用普遍方程式的方法列和公式

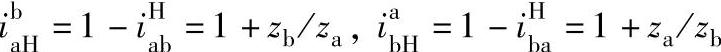
代入数据，得

3）应用“更换下标、互为倒数”方法求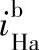和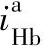

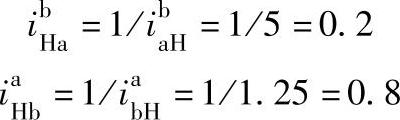
例6-2 在表6-5序号2中所示为双排内外啮合2K-H（NW）型行星轮系，已知z_a=14，z_g=38，z_f=18，z_b=70，试求传动比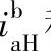和。

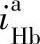解 1）转化机构传动比

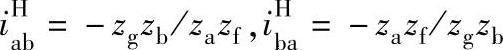
2）应用普遍方程式的方法列公式

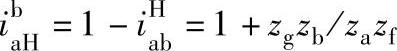
代入数据，得(https://www.xing528.com)

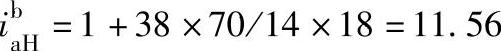
3）先应用“更换下标、互为倒数”方法，再用普遍方程式的方法列

代入数据，得

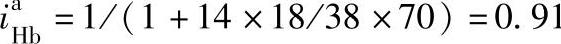
从例6-1和例6-2的计算结果可以清楚地看到，负号机构2K-H型的一些传动特性：

由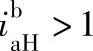、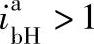和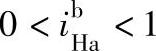、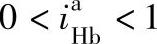，可知这种形式行星轮系的主、从动轴转向相同。行星架从动时为减速机构，主动时则为增速机构。当作减速传动时，其传动比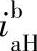或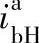都比相应转化机构传动比大1。由于|z_b/z_a|＞1，所以传动比较大，而且一定是大于2；由于|z_a/z_b|＜1，所以较小，一般在大于1至小于2之间。2K-H（NW）型转化机构为两级传动，其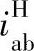较2K-H（NGW）型大，故其传动比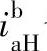也较2K-H（NGW）型大一些。

（2）正号机构2K-H型行星轮系的传动比计算 双外啮合2K-H（WW）型行星轮系（见表6-5中序号3所示）和双内啮合2K-H（NN）型行星轮系（见表6-5中序号4所示）的转化机构传动比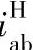均为正值，属于正号机构2K-H型行星轮系。

应用普遍方程式和“更换下标、互为倒数”的方法，不难列出这种形式的传动比公式

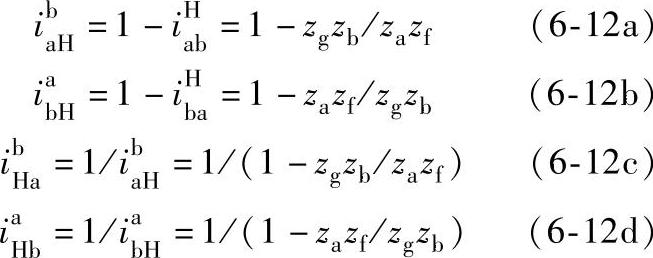
例6-3 在表6-5序号3中所示双外啮合2K-H（WW）型行星轮系，现有A、B两种规格，已知齿轮齿数分别为

规格A

z_a=41，z_g=39，z_f=41，z_b=39

规格B

z_a=100，z_g=101，z_f=100，z_b=99

试分别计算这两种规格的传动比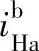和。

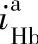解 1）转化机构传动比公式

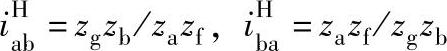
2）先应用“更换下标、互为倒数”和普遍方程式的方法，列出传动比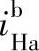和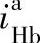

代入数据，得

规格A

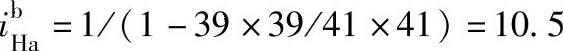
规格B

代入数据，得

规格A

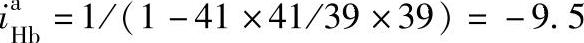
规格B

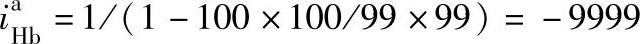
例6-4 在表6-5中序号4中所示为双内啮合2K-H（NN）型行星轮系，已知z_a=31，z_g=28，z_f=35，z_b=38，试求。

解 1）转化机构传动比公式

2）列出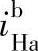公式

代入数据，得

从例6-3和例6-4的计算结果也可以清楚地看到正号机构2K-H型行星轮系的传动特性：

正号机构2K-H型行星轮系，当行星架H主动时作为减速机构，从动时作为增速机构。通常用作减速机构，其传动比可为正值，亦可为负值。如例6-3中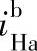=10.5，主、从动构件转向相同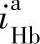；=-9.5，主、从动构件转向相反，传动比的绝对值变化范围很大。当转化机构传动比公式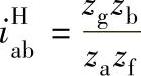中，分子和分母的比值较接近于1，而且齿数都较大时，则行星轮系传动比的绝对值就越大。如例6-3规格B，其传动比竟达到10000。