如何计算转化机构中的传动比？

行星齿轮传动系为动轴线传动，其传动比的计算不能简单地用定轴传动的公式计算，而通常采用行星架固定法、图解法、矢量法、力矩法等。其中最常用的是行星架固定法，现叙述如下：

1）符号规定。传动比

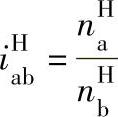
式中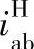——构件H固定、a主动、b从动时的传

动比；

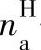——构件H固定、主动构件a的转速；

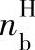——构件H固定、从动构件b的转速；

上标H——固定构件代号；

下标a——主动构件代号；

下标b——从动构件代号。

2）应用行星架固定法计算行星齿轮传动的传动比。行星架固定法就是设想将行星轮系通过机构转化为过桥，来确定行星轮系的传动比，故又称转化机构法，首先是威尔斯（Willes）于1841年提出的。

行星架固定法系根据理论力学相对运动的原理，即“一个机构整体的绝对运动并不影响机构内部各构件中间的相对运动”。这正如一只三针手表中的秒针、分针和时针的相对运动关系不因带表人的行动变化而变化。

图6-2所示的2K-H（NGW）型行星传动中，设两个中心轮a、b和行星架H的转速分别为n_a、n_b和n_H，行星轮g的转速为n_g，同时设各轮的转向相同，并取顺时针转动方向为正。现给整个行星轮系加一个与行星架H转速大小相等方向相反的附加转速（-n_H），按上述相对运动原理，并不影响2K-H型行星轮系中任意两构件间的相对运动关系。以观察者来看，轮系中各构件转速关系见表6-4。

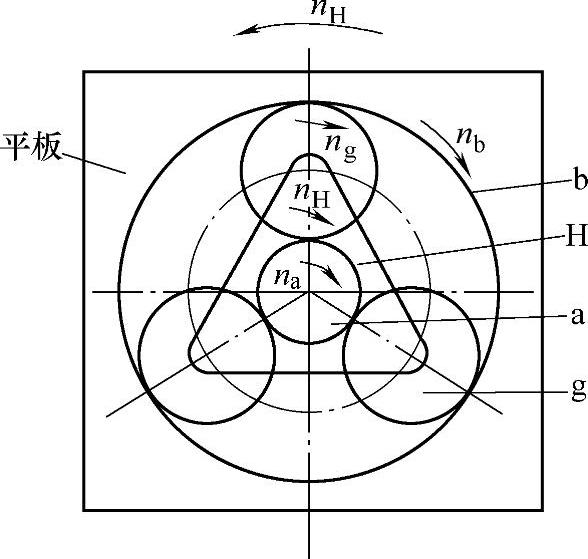
图6-2 2K-H（NGW）型行星齿轮传动法及其转化机构

由表6-4可以看出，原来运动的行星架变为静止的支架，于是行星轮系转化为转化机构。在转化机构中，各构件的转速为n^H_H、n^H_a、n_g^H、n_b^H，表示为相对于行星架的转速，这样转化机构中任意两轮的传动比，就可以用定轴轮系的方法计算。设中心轮a、b分别为转化机构的主、从动轮，则得其传动比为

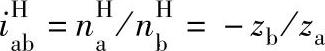
将两个中心轮转化前后的转速关系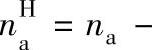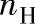、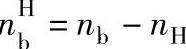代入转化机构传动比公式，即可得到行星轮系各基本构件的转速关系

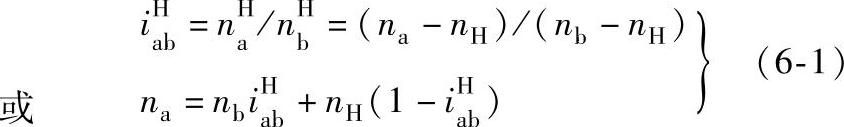
表6-4 给整个行星轮系一个附加转速（-n_H）后，各构件的转速变化式

显然，式（6-1）中的转化机构传动比i^H_ab是容易求得的。因此，式（6-1）列出了行星传动轮系中三个基本构件转速n_a、n_b和n_H的关系式。应用式（6-1）不难求得当任一基本构件固定时，其他两个基本构件之间的传动比。

当中心轮b固定、中心轮a主动，行星架H从动时，这时用n_b=0代入式（6-1）得

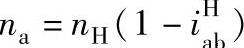
移项整理得(www.xing528.com)

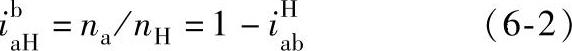
当中心轮（太阳轮）a固定、中心轮（内齿圈）b主动、行星架H从动时，这时用n_a=0代入式（6-1）得

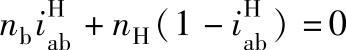
移项整理得

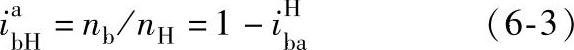
应用行星架固定法分析行星传动运动学，其概念清晰，应用灵活，但要注意如下几个问题：

①转化机构的传动比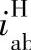按定轴轮系传动比的计算方法进行计算，但要特别注意其正负号。当转化机构的传动比为正值，即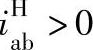时，称为正号机构；当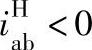时，则称为负号机构。表6-5中列出了各种2K-H型行星轮系的传动比和转化机构传动比。

转化机构的传动比对行星轮系传动比有直接的影响。对负号机构，将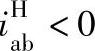代入式（6-2），即可得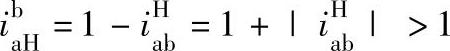。这说明负号机构行星轮系的主、从动构件转向相同，行星轮系传动比比相应转化机构传动比只大1。对正号机构，将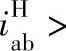0代入式（6-2）求得行星轮系传动比，其值可能为正，也可能为负，即主、从动构件的转向可能是同向，也可能是反向。当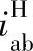接近于1时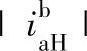，趋于很小值，其倒数的绝对值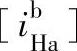却很大，可见正号机构，当行星架主动时，不难设计出传动比达数千以上的减速机构。

②行星架固定法的转速关系式，是建立在各构件转速方向相同的基础上，因此在应用时，如果某一构件的实际转向与假设不符时，则应以负值代入；如果应用转速方程式计算得到的转速为负值时，则说明其转速方向与假设方向相反。

③行星架固定法的应用很灵活。式（6-1）只是应用行星架固定法列出的一个方程式，同理也可以列出

行星架固定法列出的转速关系方程式，既可用于求行星轮系中任意两基本构件间的传动比和封闭行星轮系的传动比，也可用于确定差动轮系中三个基本构件的转速关系。

行星架固定法还可以列出包括非基本构件行星轮g的转速n_g在内的转速关系，如

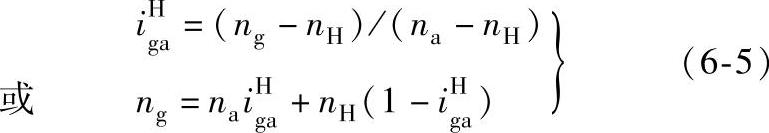
式（6-5）用于计算行星轮g的转速n_g，移项后还可以求得行星轮g相对于行星架H的转速

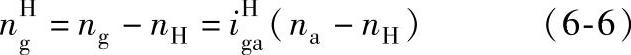
④由于行星架固定法应用了转速的代数合成，因此，它只适用于圆柱齿轮组成的行星轮系。但对于由锥齿轮组成的行星轮系，虽属于空间轮系，由于其三个基本构件的转动轴线均重合于轮系的主轴线，因此这三个基本构件仍然可以应用行星架固定法来建立转速关系式。不过应该注意的是，在计算转化机构传动比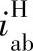时，其正负号应按画箭头的方法来确定。显然，对锥齿轮2K-H型，不能用于行星架固定法列出包括行星轮在内的转速关系式。

对于分析计算齿轮轴线不是平行于主轴线的齿轮转速，只能应用矢量图解法进行分析求解。

3）行星轮系传动比计算的普遍方程式。对构件回转轴线重合或平行的行星轮系，根据威尔斯提出的行星架固定法基本原理——相对运动原理，可以不限于行星架固定法，可以扩大到所涉及三构件中任一构件的固定法来列其转速关系式。例如，行星轮系三个基本构件的转速关系式，可按构件A固定法列出式（6-7），也可按构件B固定法列出式（6-8），即

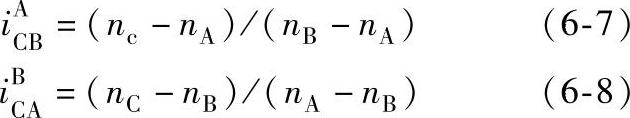
移项相加得

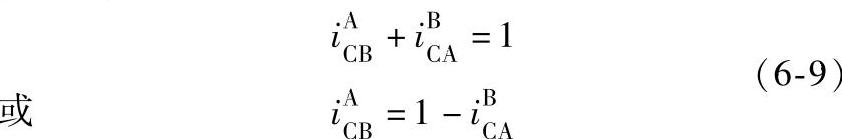
在式（6-9）中，符号A、B、C可以任意代表行星轮系中的三个基本构件。式（6-9）的形式和行星架固定法求行星轮系传动比式（6-2）、式（6-3）一样。式（6-9）就是计算行星轮系传动比的普遍方程式。这是一个有规律的、很容易记住的公式，在等式左边i的上标和下标可以根据计算需要来标注，将其上标与第二个下标互换位置，则得到等号右边i的上标、下标号。