锥齿轮传动的几何计算方法探讨

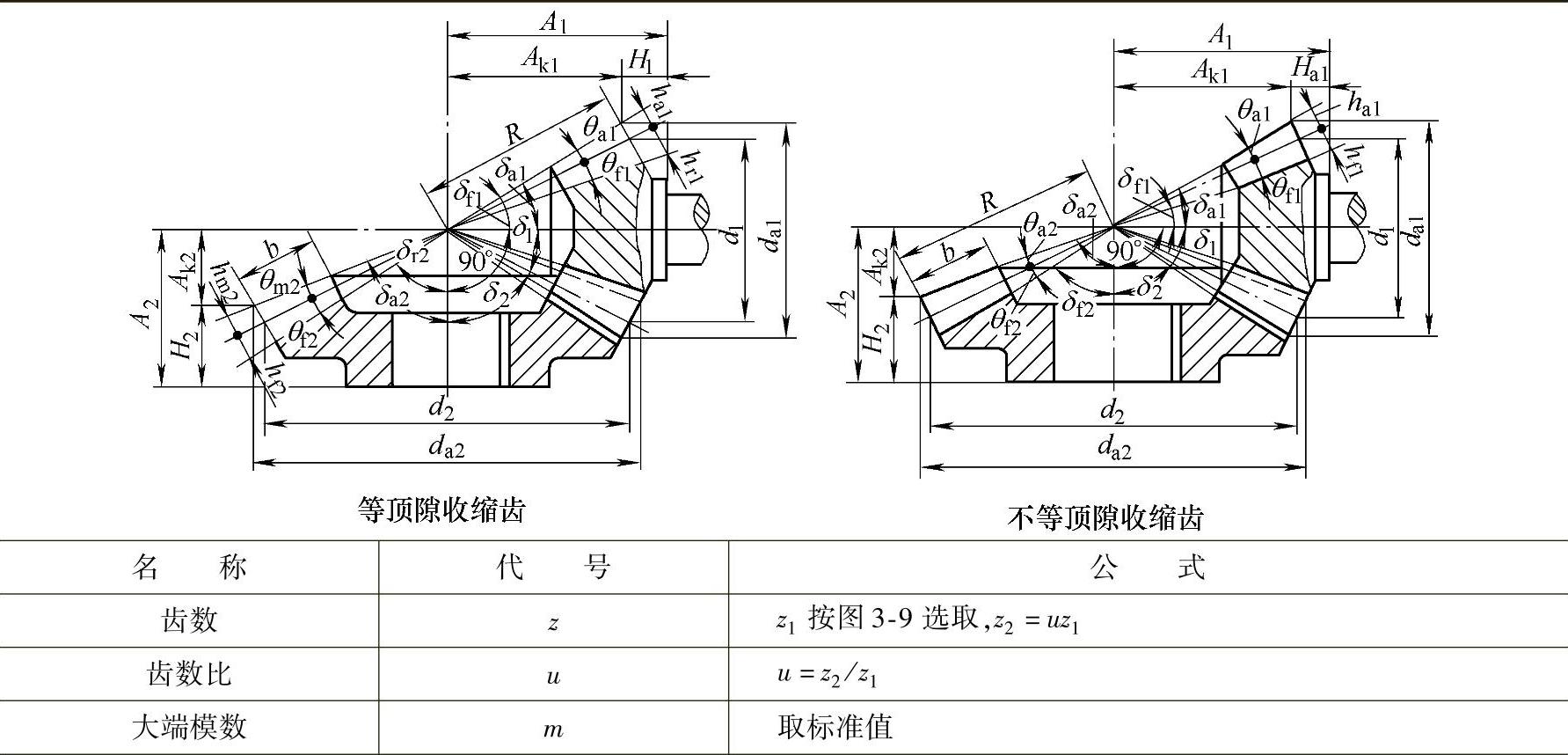
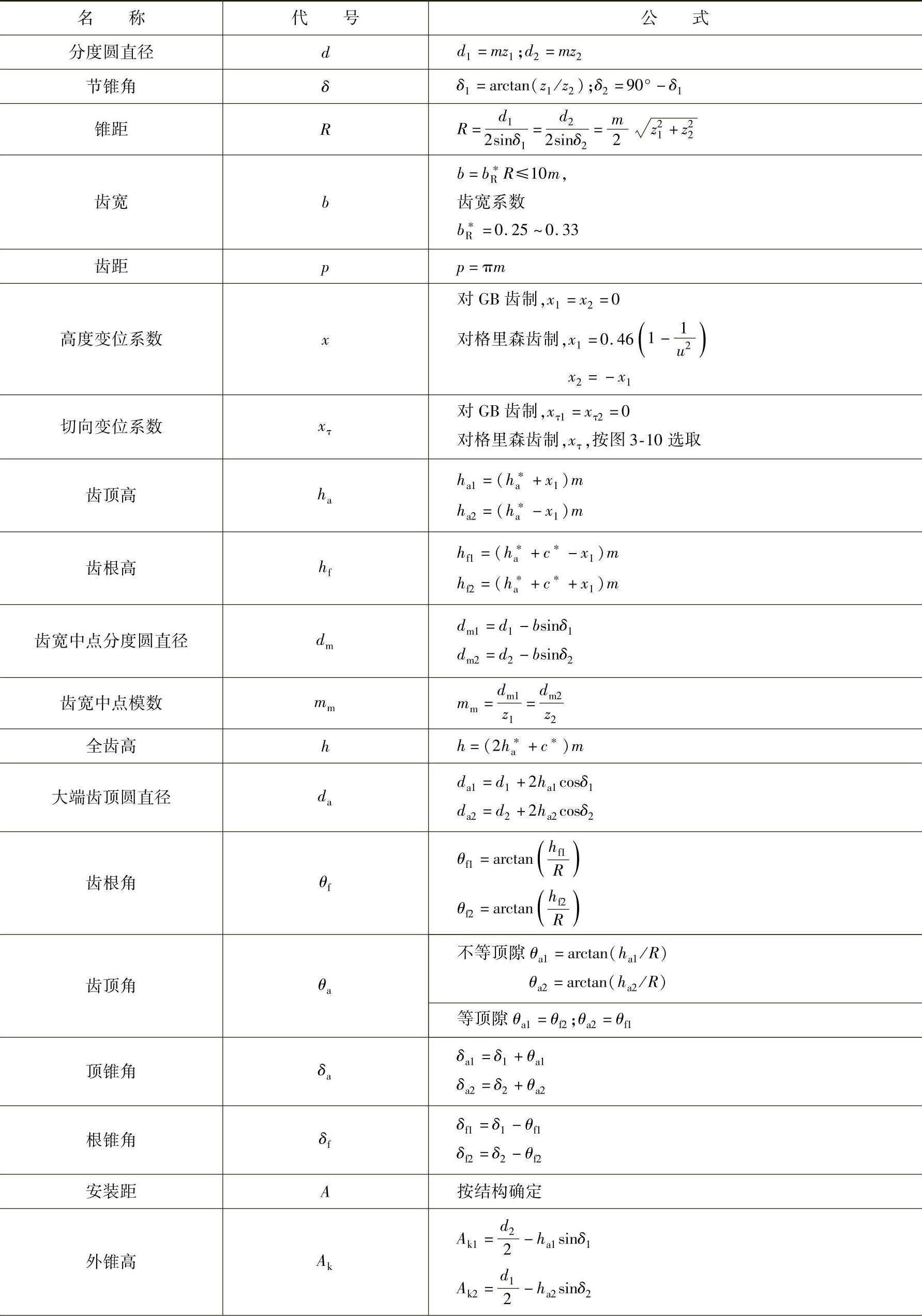
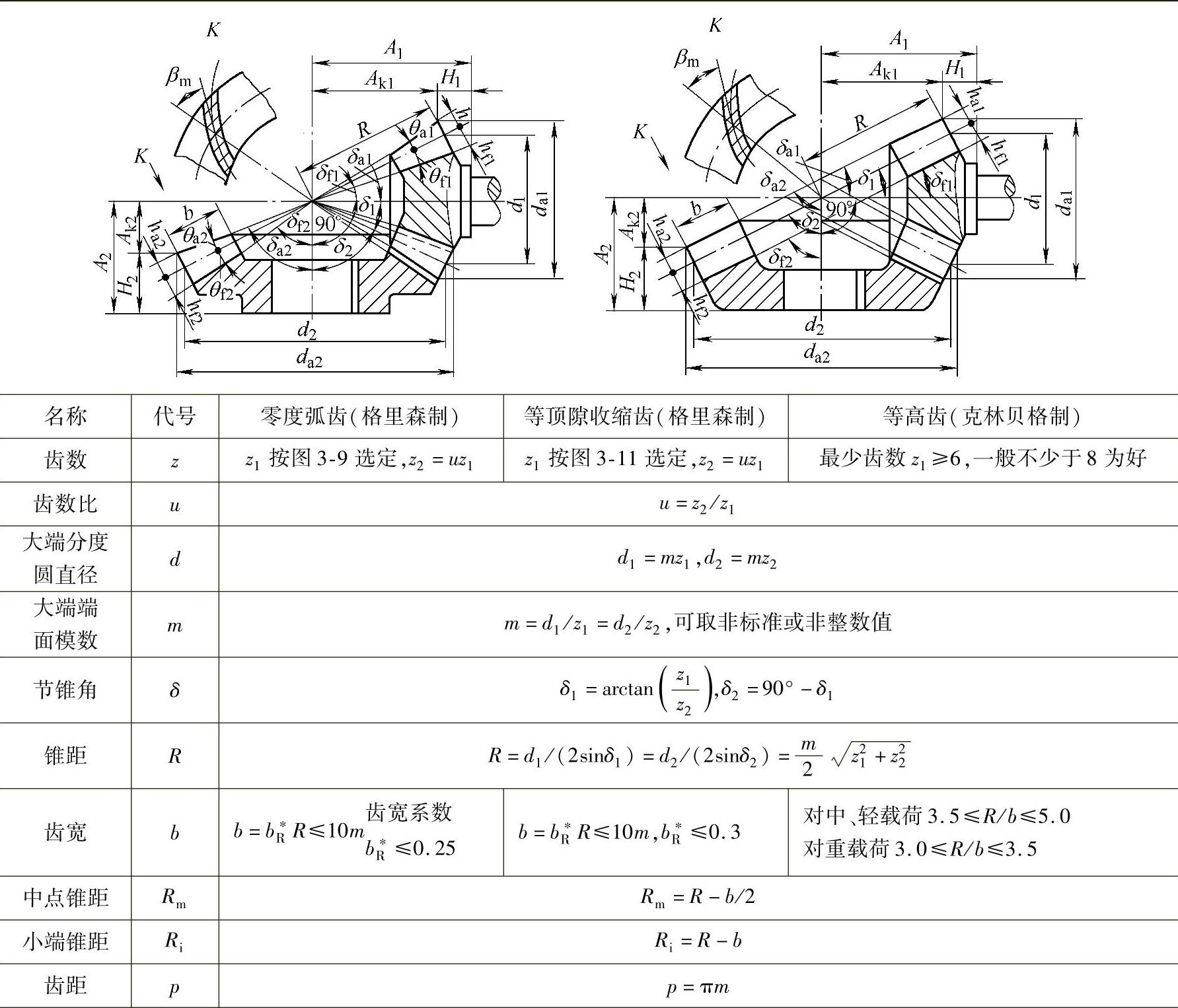
直齿锥齿轮正交传动的几何计算见表3-13，曲线齿锥齿轮正交传动的几何计算见表3-14，z₁＜12，α=20°，β_m=35°～40°的弧齿锥齿轮参数见表3-15，锥齿轮不同传动比时大小轮的最少齿数见表3-16。

表3-13 直齿锥齿轮正交传动的几何计算

（续）

（续）

表3-14 曲线齿锥齿轮正交传动的几何计算

（续）

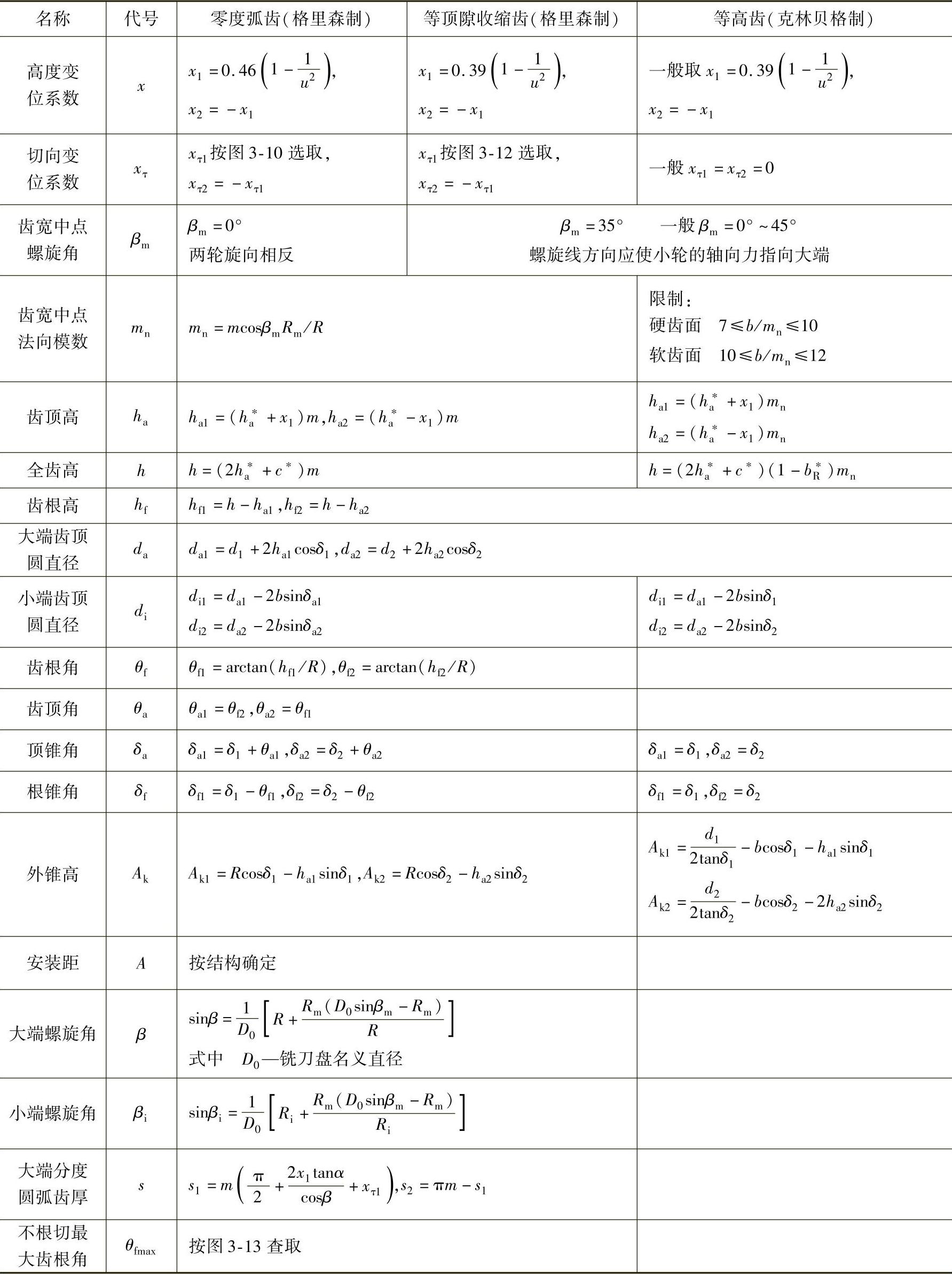
注：1.克林贝格机床加工的齿轮参数还必须满足R_msinβ_m＜r＜Rsinβ的关系式，r为刀盘半径。

2.克林贝格齿制的大、小端螺旋角、弧齿厚计算和不根切等校核及为改善传动性能所作的修整计算的公式繁多，有些和刀具及机床调整参数有关。需要时可请制造厂帮助核算。

表3-15 z₁＜12，α=20°，β_m=35°～40°的弧齿锥齿轮参数

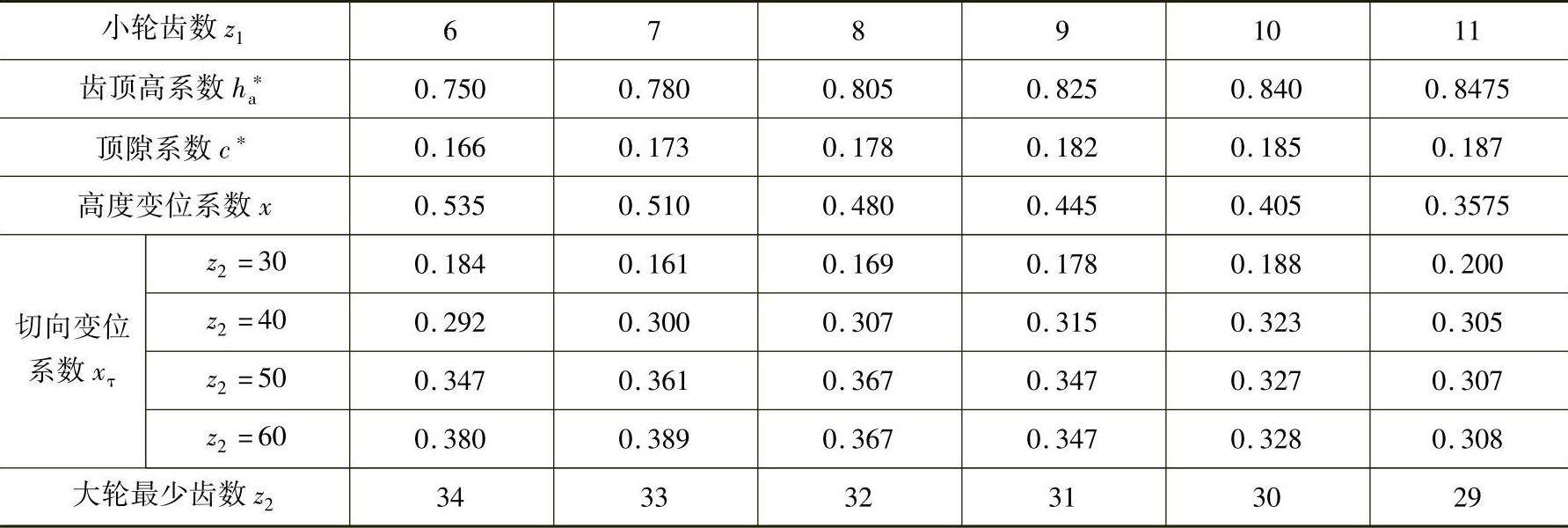
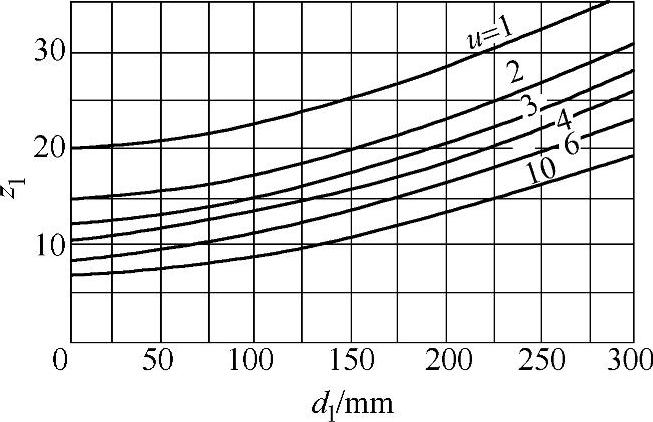
图3-9 直齿及零度弧齿锥齿轮小轮齿数z1

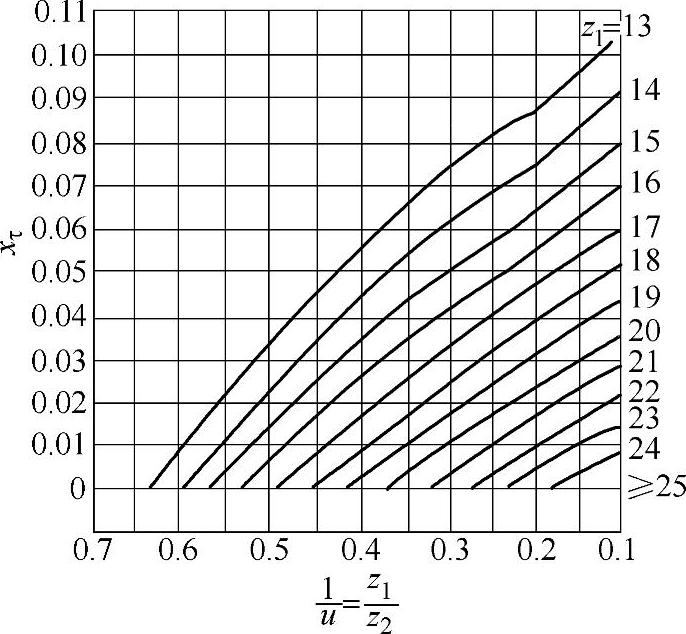
图3-10 直齿及零度弧齿锥齿轮切向

图3-11 弧齿锥齿轮小轮齿数z₁（β_m=35°）

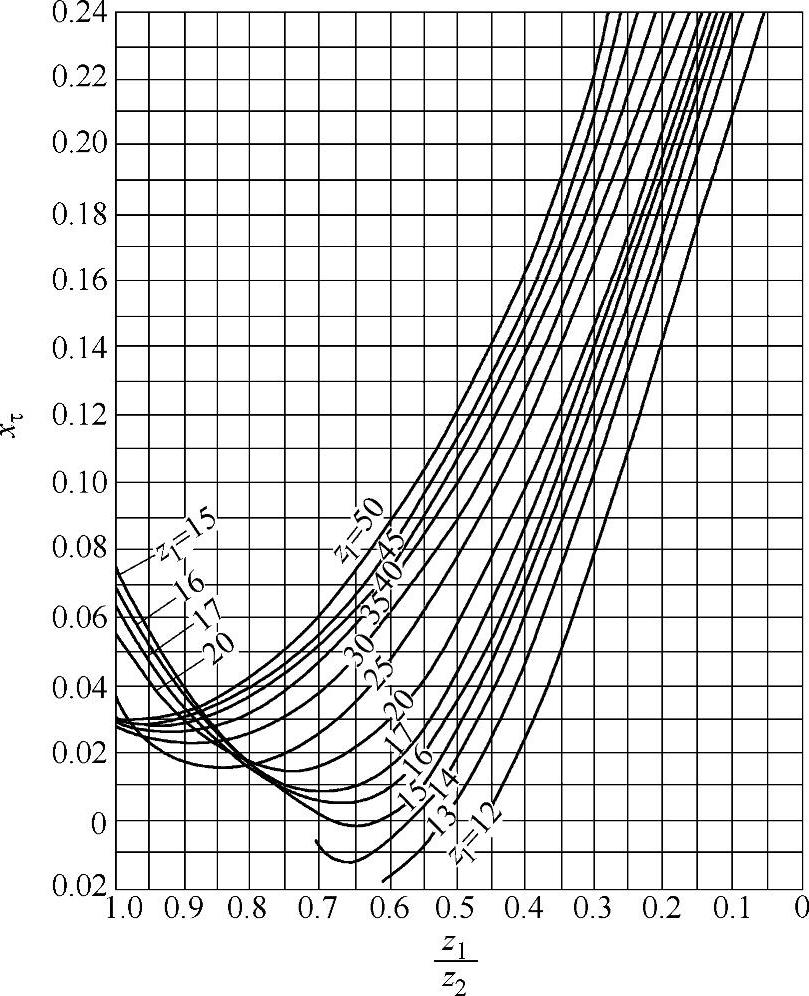
图3-12 弧齿锥齿轮切向变位系数xτ（格里森齿制）

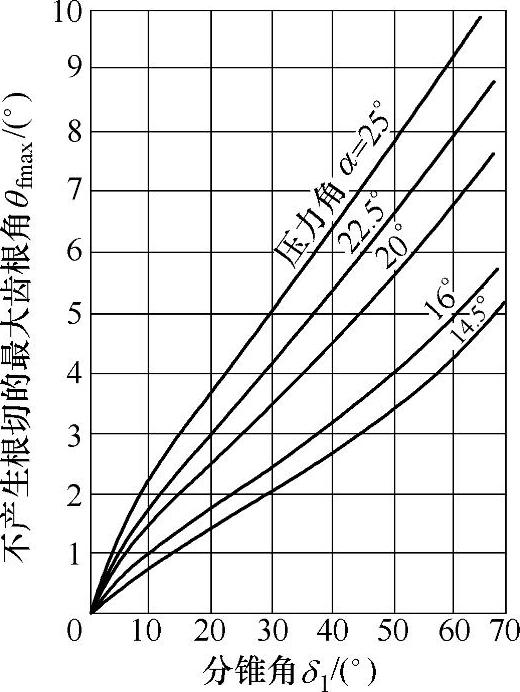
图3-13 弧齿锥齿轮β=35°时不产生根切的最大齿根角

表3-16 锥齿轮不同传动比时大小轮的最少齿数（齿形角20°）

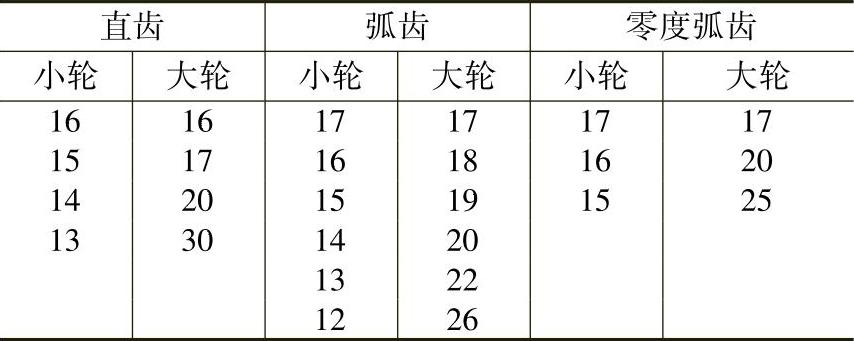
由于直齿锥齿轮几何计算时，涉及许多角度值计算。特别是精确计算，角度要算到秒（1″），三角函数值要查八位数。为了便于实际应用，今将直齿锥齿轮简化为表3-17，并配合公式查表便可。

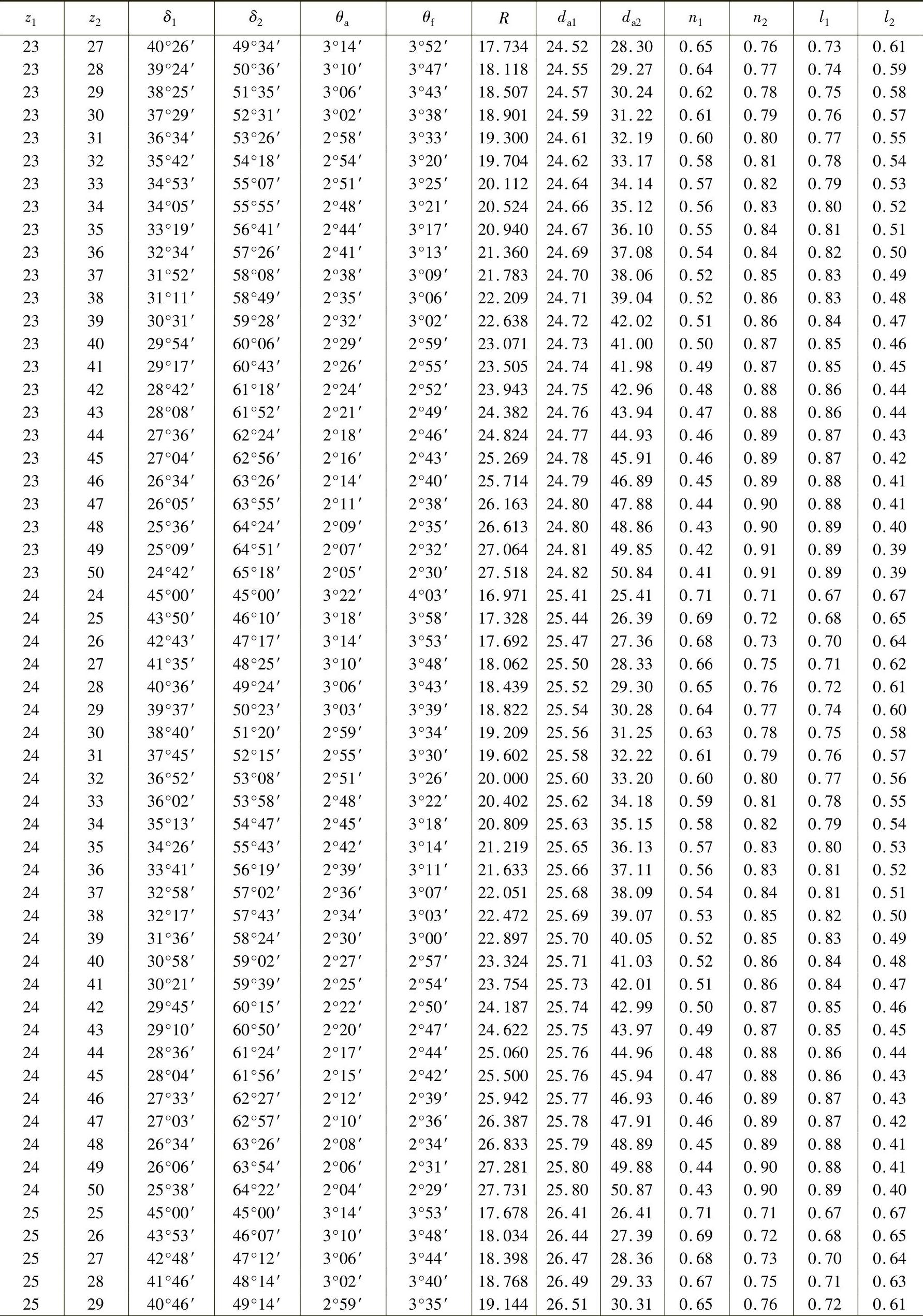
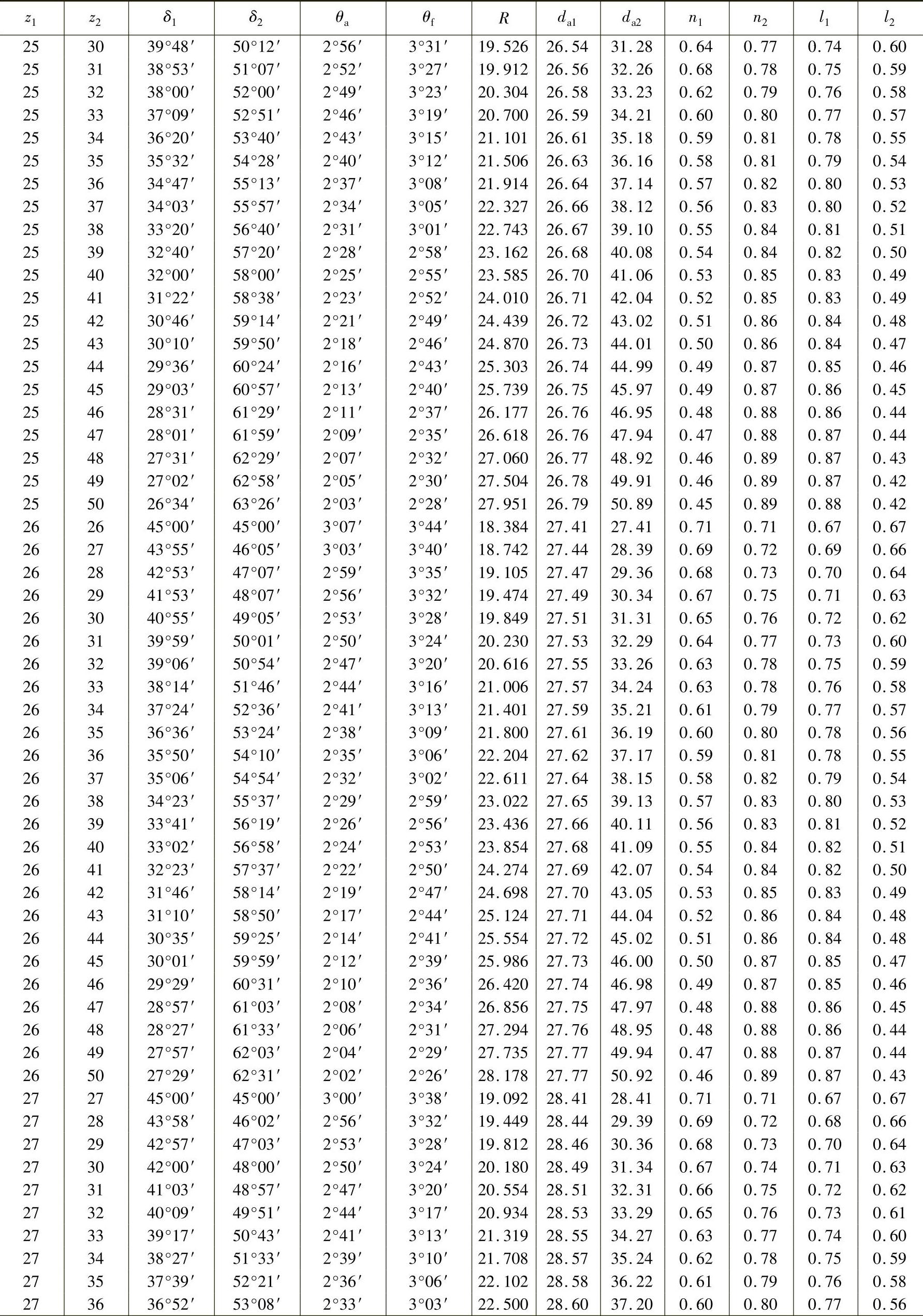
例3-1 某减速器中有一对直齿锥齿轮，已知轴交角Σ=90°，模数m=10mm，小齿轮z₁=19，大齿轮齿数z₂=38，压力角α=20°，齿顶高系数h_a∗=1，顶隙系数c∗=0.2，试确定该对齿轮的各部分尺寸。

解：根据z₁=19，z₂=38，查表3-17得

δ₁=26°34′，δ₂=63°26′，θ_a=2°42′，θ_f=3°14′，R=21.243mm，d_a1=20.79mm，d_a2=38.89mm，n₁=0.45mm，n₂=0.89mm，l₁=0.87mm，l₂=0.41mm。

1）分度圆锥角（查表3-17）

δ₁=26°34′，δ₂=63°26′

2）分度圆直径：

d₁=mz₁=10×19mm=190mm

d₂=mz₂=10×38mm=380mm

3）锥距R（查表3-17表值×m）

R=21.243×10mm=212.43mm

4）齿宽b：

b=R/3=212.43mm/3=70.81mm，取b=70mm或65mm

5）齿顶圆直径（查表3-17表值×m）

d_a1=20.79×10mm=207.9mm

d_a2=38.89×10mm=388.9mm

6）齿顶角（查表3-17表值）

θ_a=2°42′

7）齿根角（查表3-17表值）(www.xing528.com)

θ_f=3°14′

8）顶锥角（查表3-17表值δ+θ_a）δ_a1=δ1+θ_a=26°34′+2°42′=29°16′（1°=60′）

δ_a2=δ2+θ_a=63°26′+2°42′=66°08′

9）根锥角（查表3-17表值-θ_f）

δ_f1=δ1′-θf=26°34′-3°14′=23°20′

δ_f2=δ2-θf=63°26′-3°14′=60°12′

10）冠顶距：

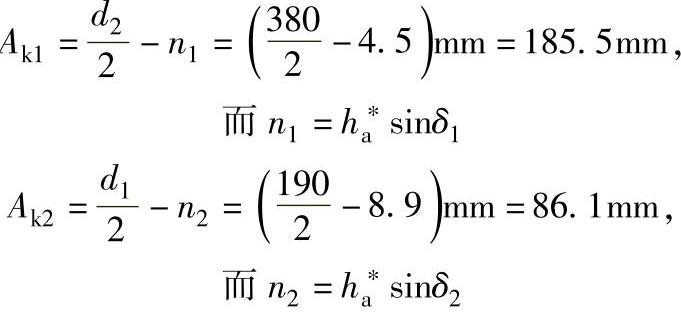
11）齿宽的影高（查表3-17表值×b）

l₁=0.87×70mm=60.9mm

l₂=0.41×70mm=28.7mm

12）齿顶高的影高（查表3-17表值×m）

n₁=0.45×10mm=4.5mm

n₂=0.89×10mm=8.9mm

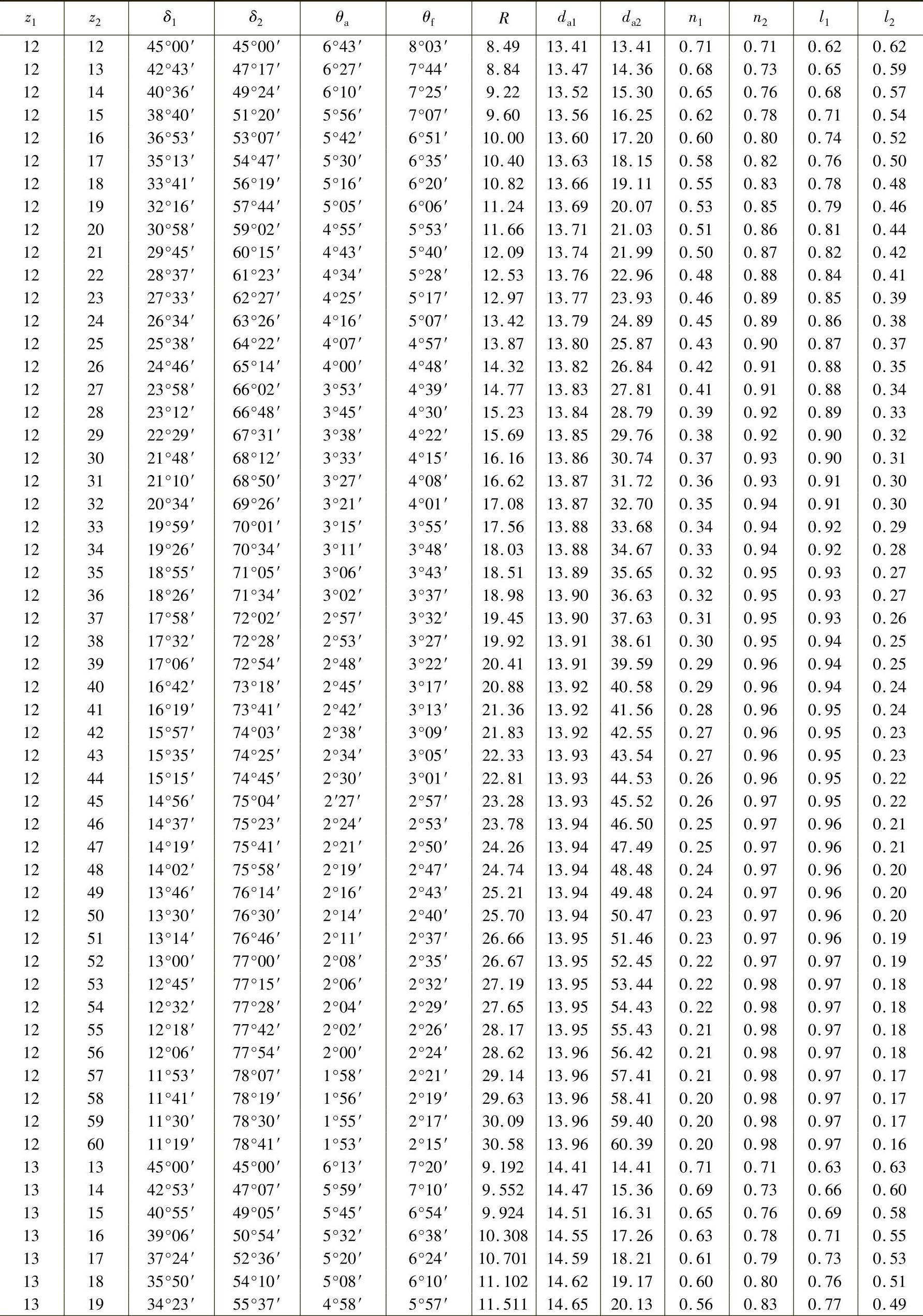
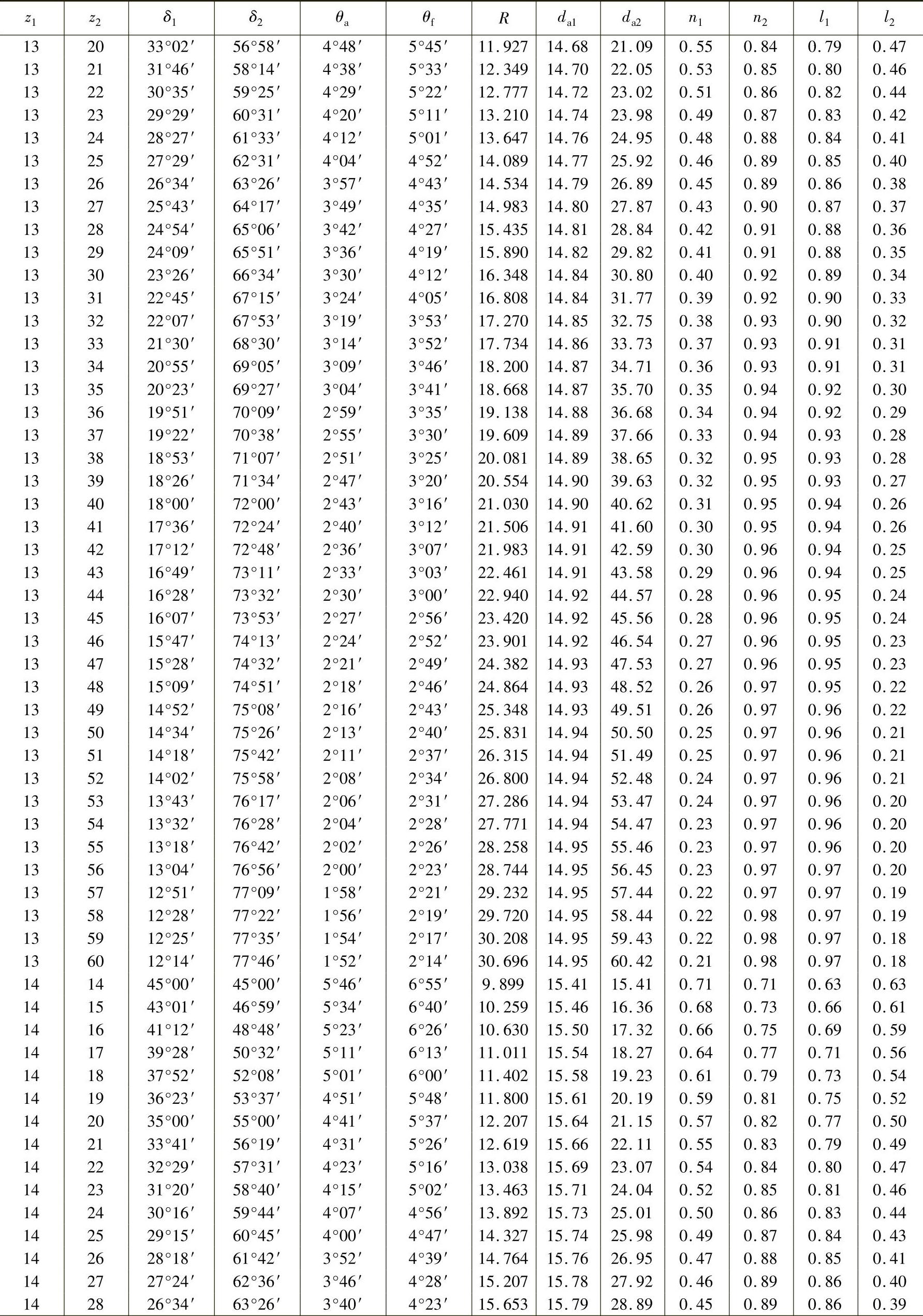
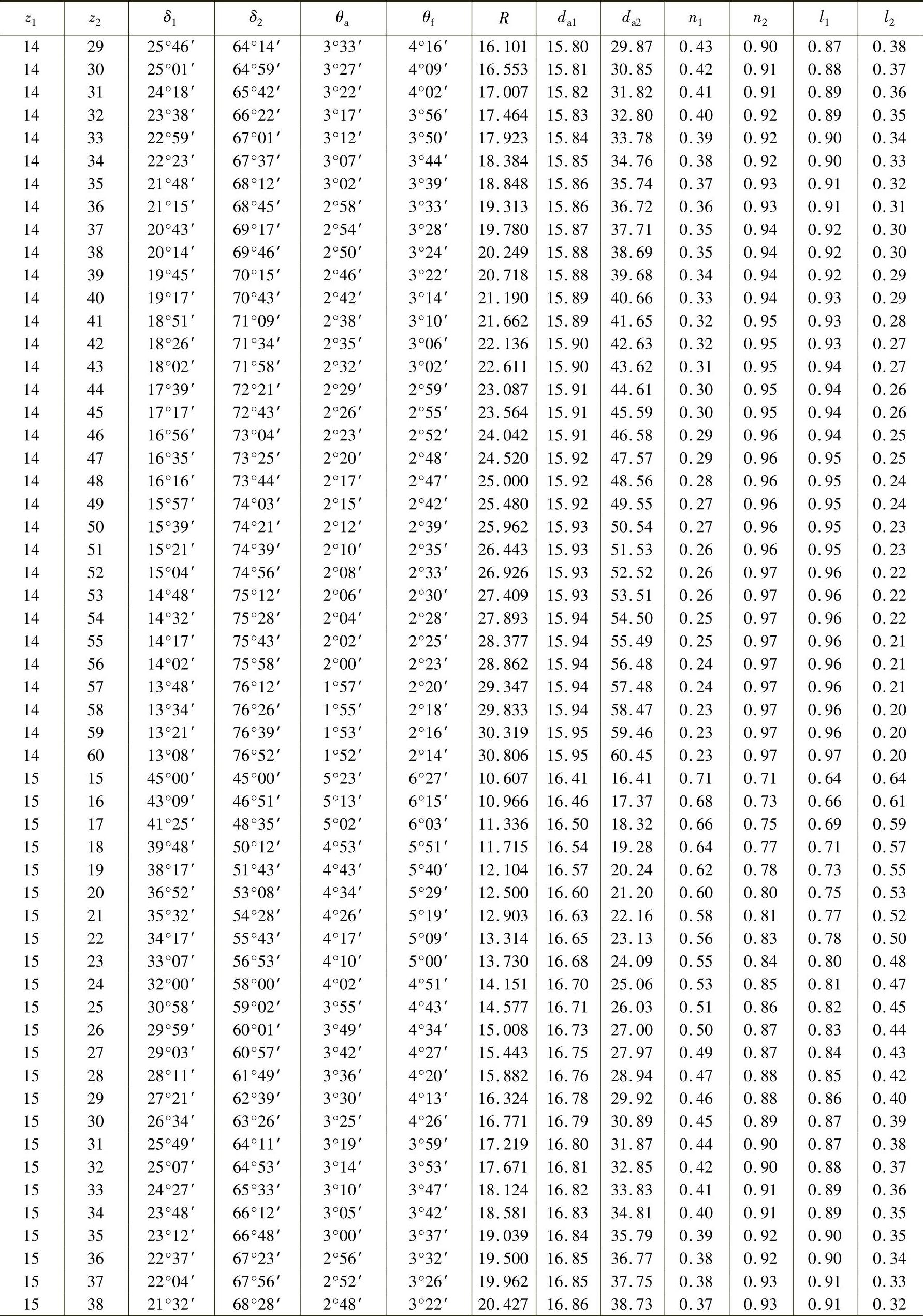
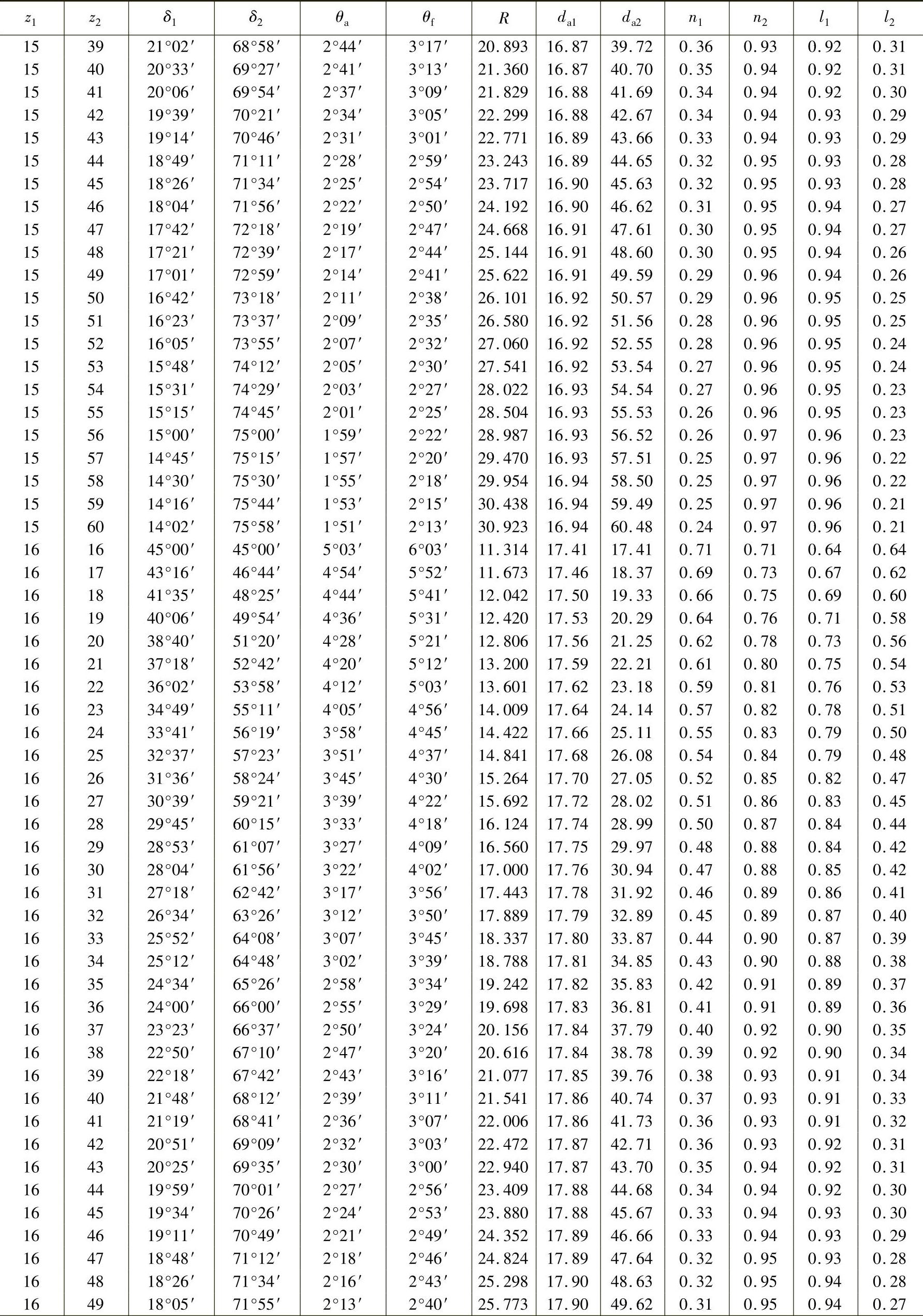
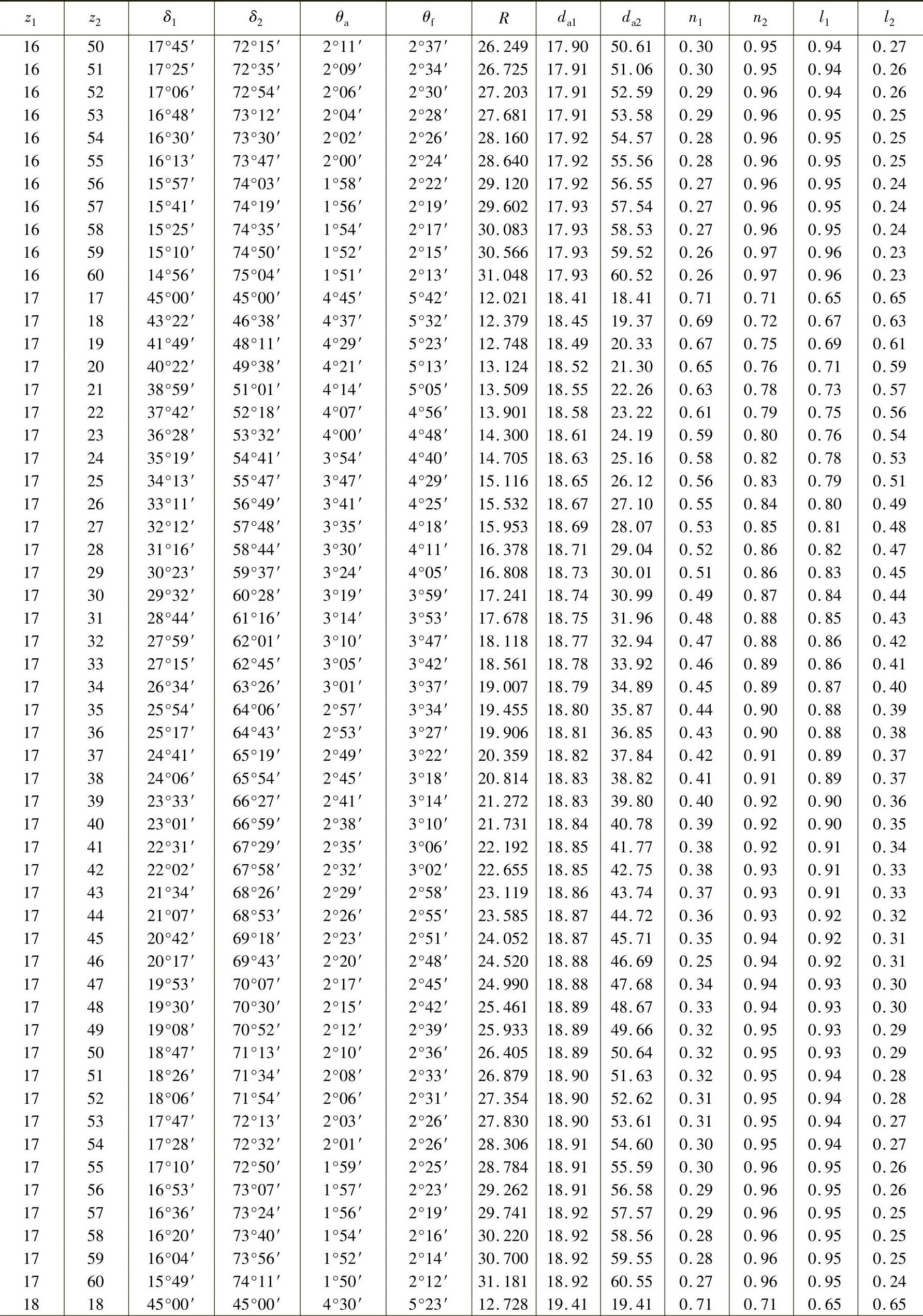
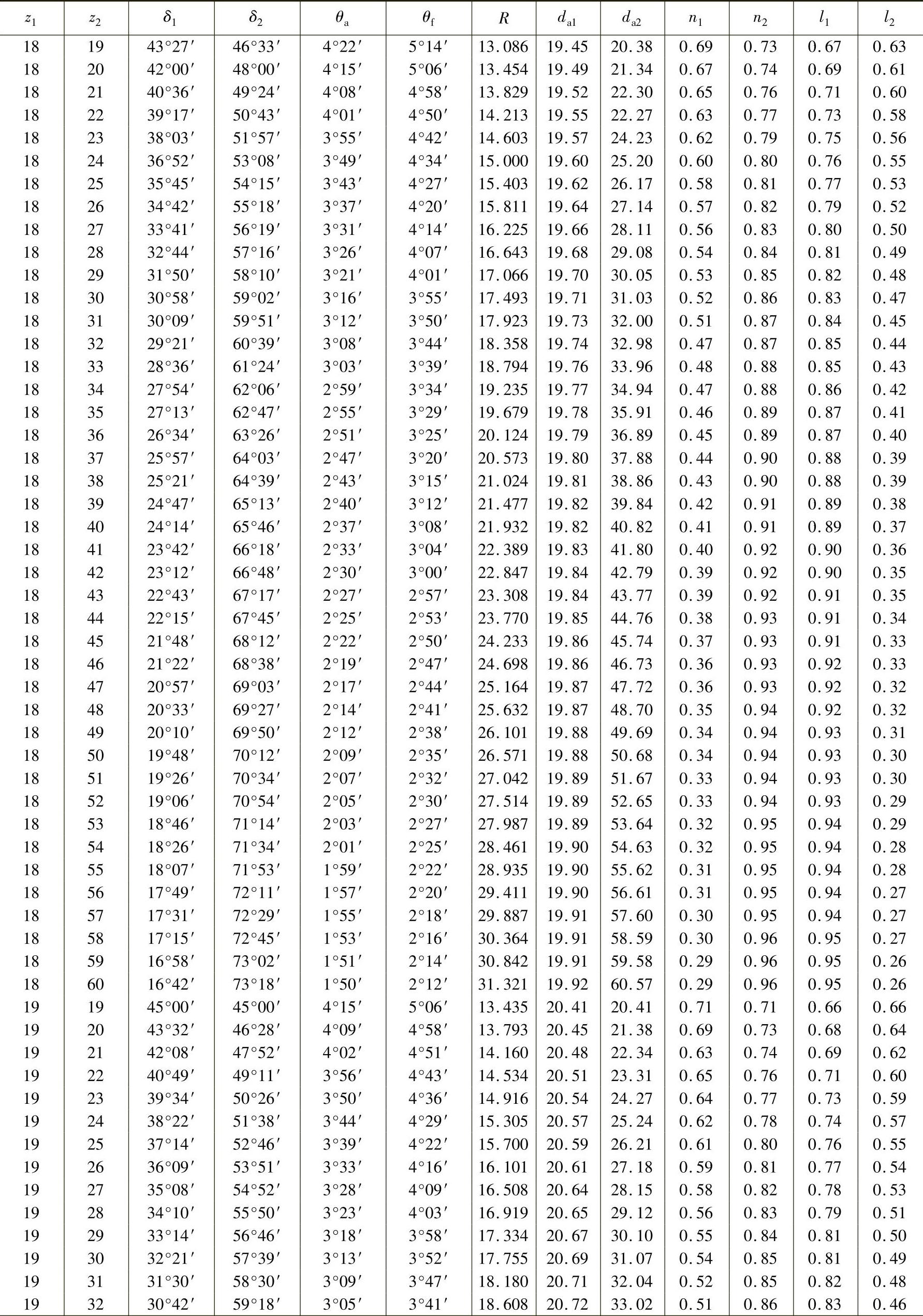
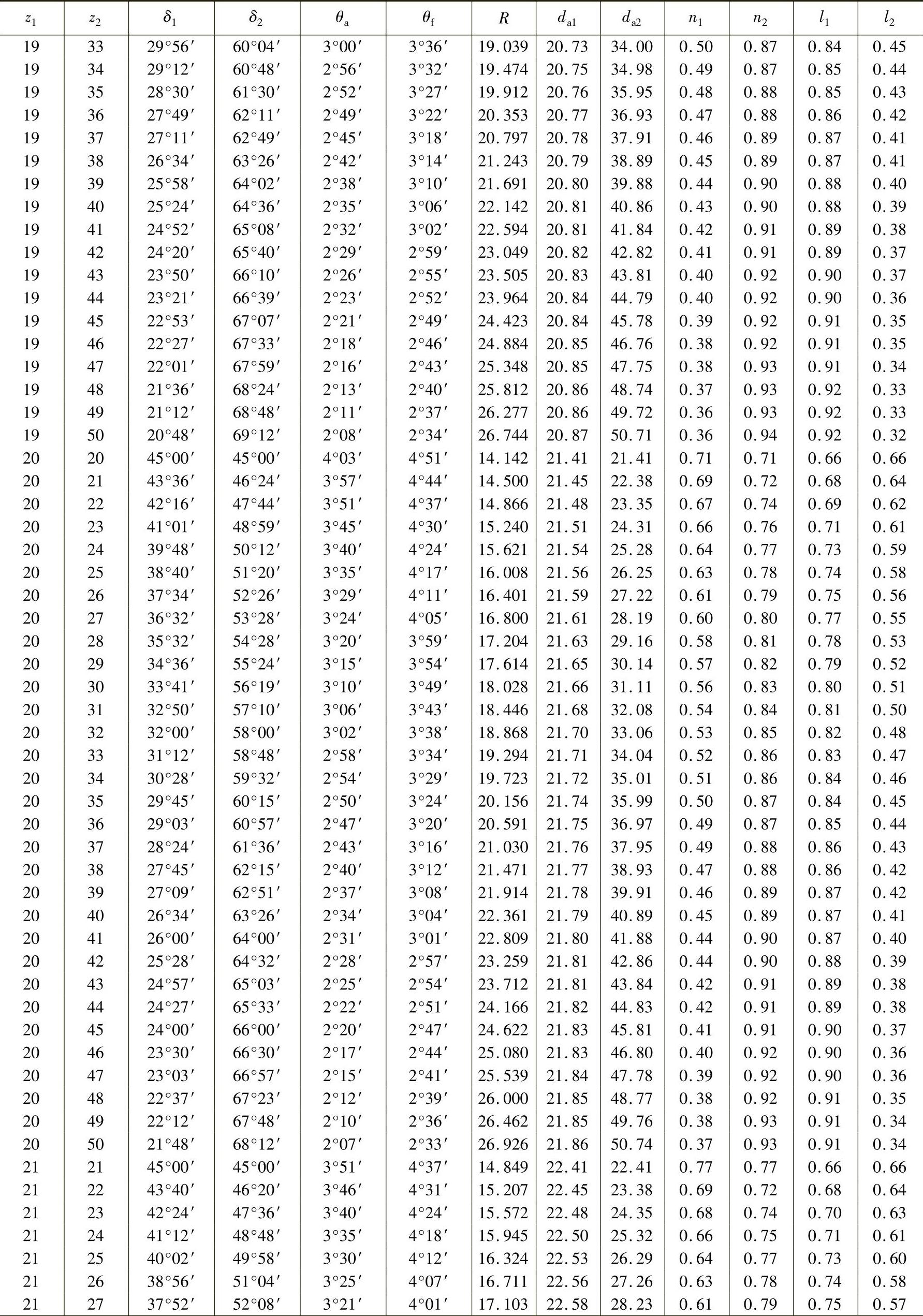
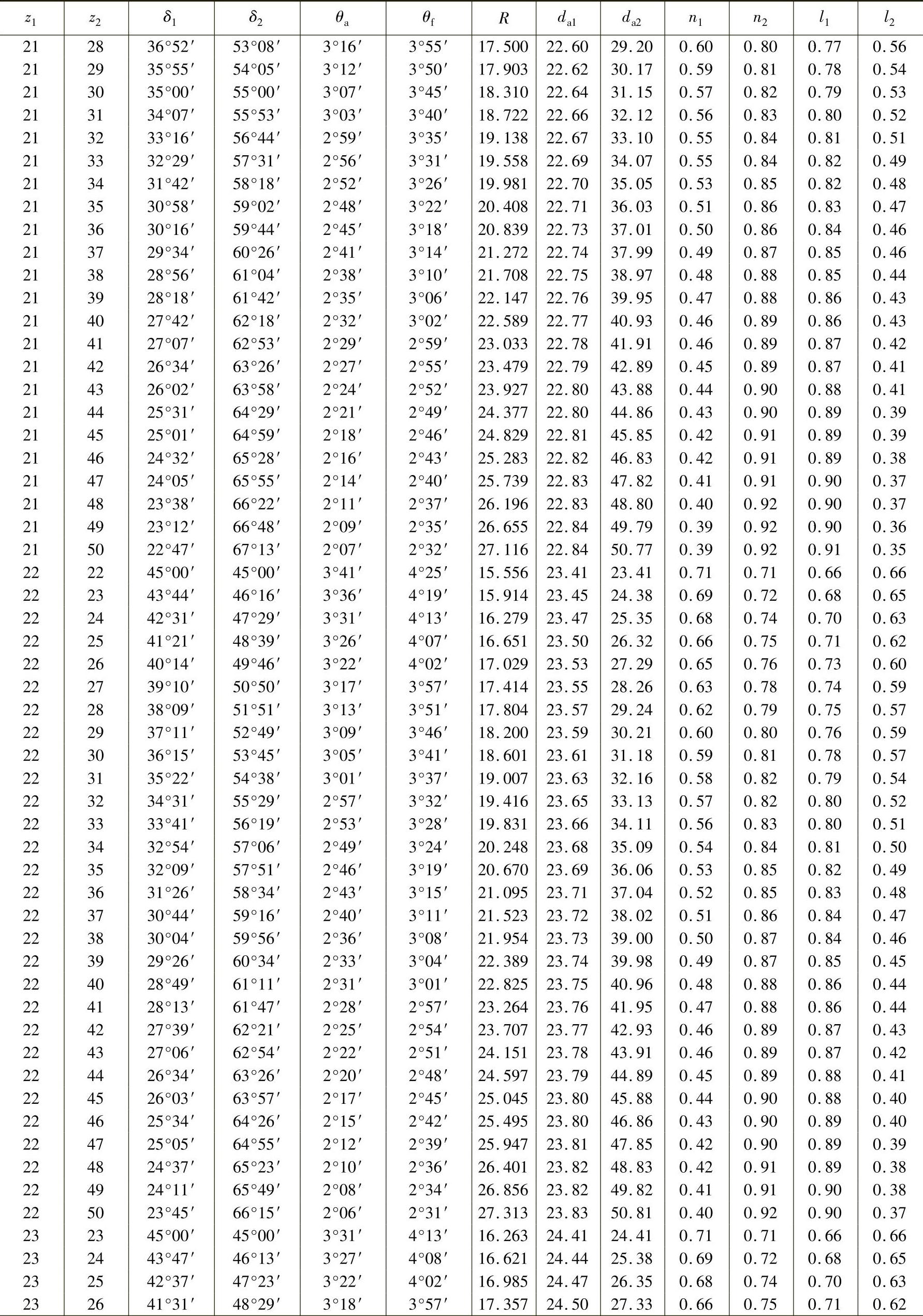
表3-17 轴交角Σ=90°时锥齿轮各部分的基本尺寸（小齿轮齿数z₁=12～30、m=1mm，h_a∗=1、c∗=0.2） （单位：mm）

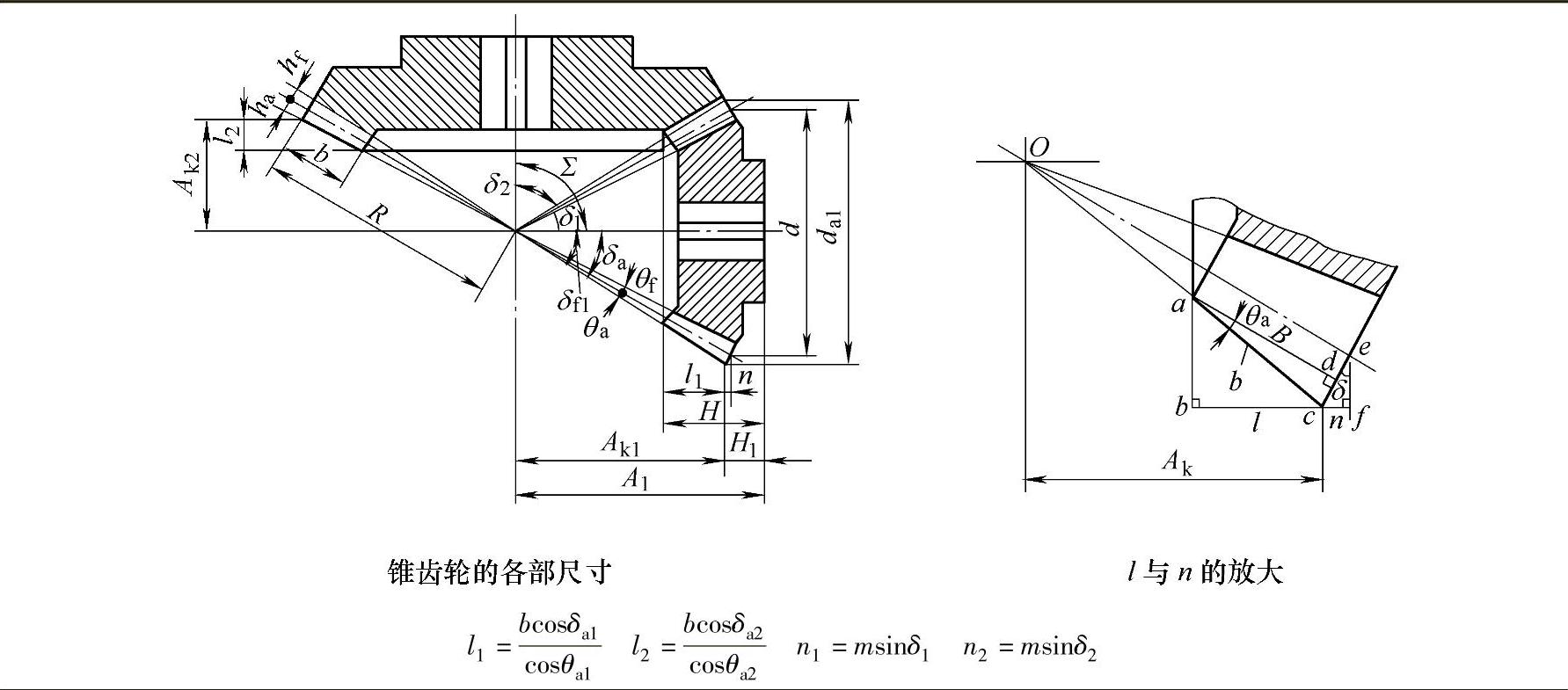
如果结构确定了H值，则安装距A便可确定。

（续）

（续）

（续）

（续）

（续）

（续）

（续）

（续）

（续）

（续）

（续）

（续）

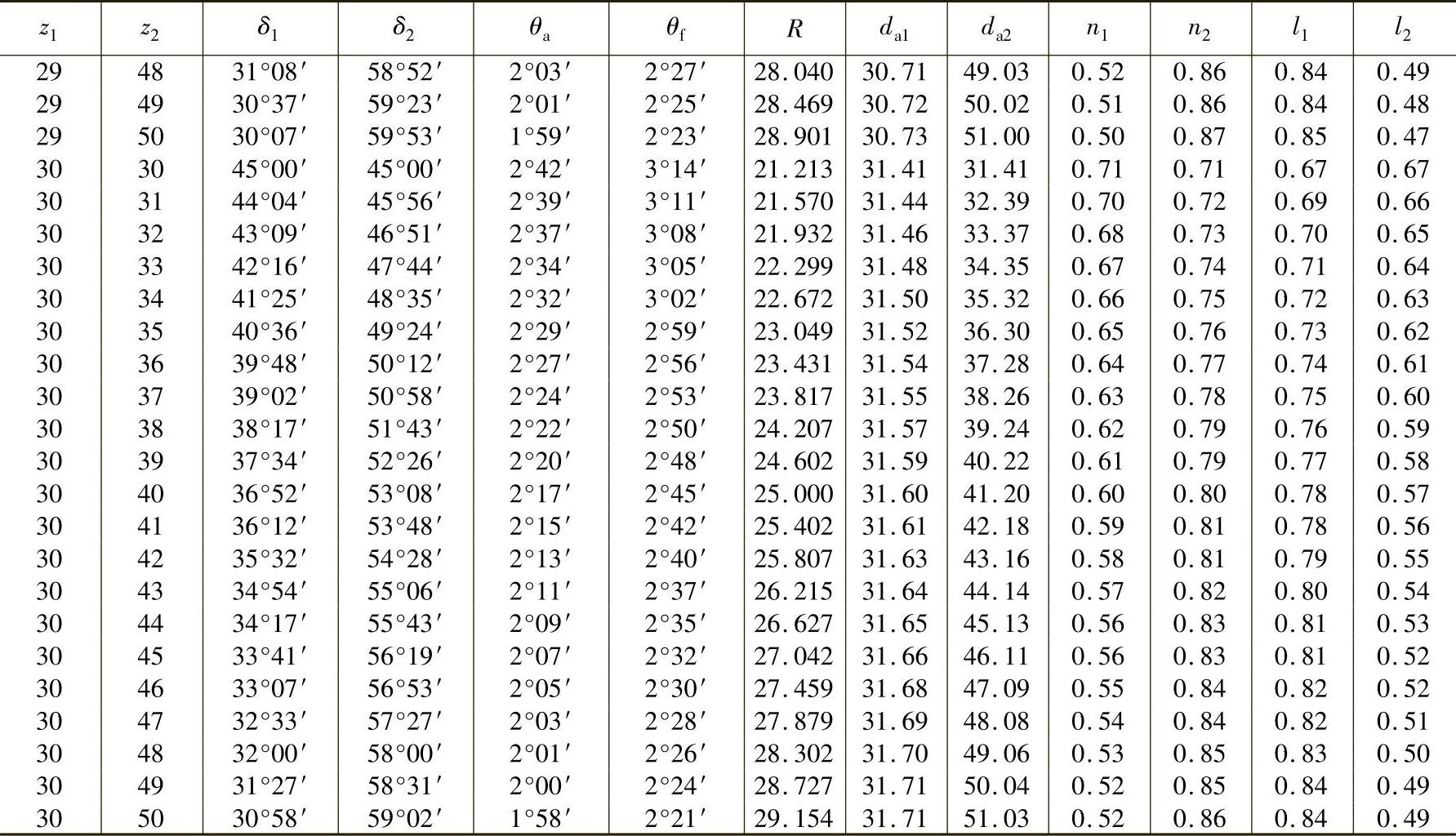
注：1.本表数值适用于所有齿形角α的齿轮，但h_a∗=1，c∗=0.2。而m≠1mm时，而R、d_a及n均须相应增减。如D_p=10mm，即m=2.54mm时，则R、d_a及n等值均须乘以2.54。

2.表中l是b=1mm时计算的。如计算的齿轮b=14mm，则l值须乘以14。

3.当计算齿轮c∗≠0.2时，则θ_f值须另行计算。当h_a∗≠1时，则θ_a、θ_f、d_a、n及l值均须另行计算。