并行性分析：探讨并发执行的效率

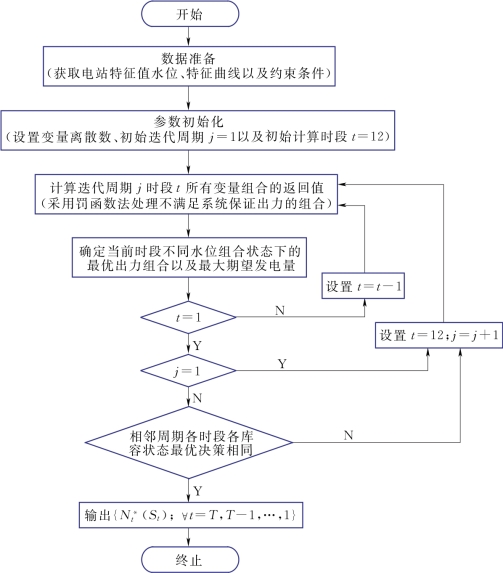
图9.2　SDP算法流程图

SDP方法求解梯级水电站群长期发电优化调度问题优化结果是各时段各蓄水状态组合下的最优决策出力组合。根据SDP递推公式（9.1），求解过程中需对电站蓄水状态St、径流Qt以及决策出力Nt进行离散，计算各变量组合状态下的梯级水电站群期望发电量，并逐时段递推寻优，直至相邻调度周期同时段同蓄水状态组合下的最优决策出力组合均相同。以单库最优决策出力递推过程为例，见图9.3。图9.3中，蓄水状态离散个数为L，入库流量离散个数为G，决策出力离散个数为C。对于任意离散值每个离散决策出力（图中蓝实线表示红虚线表示在不同的离散入库径流下，均需返回G个不同结果图9.3中表示计算末水位对应的余留效益函数，通过插值求得]，即需完成G次计算任务，才可求得初始蓄水状态决策出力的全时期（时段t到时段T）期望发电量。因此，推求初始蓄水状态的最优决策出力需完成G×C次计算任务，而单时段内所有蓄水状态的最优决策出力，则需完成L×G×C次计算任务。同理，若水电系统计算电站数目为M，则求解单时段最优决策出力组合需计算（L×G×C）M次。若蓄水状态离散个数为40，入库流量离散个数为10，决策出力离散个数为10，求解1个水电站单个时段内所有蓄水状态的最优决策出力则需完成4×103次计算任务，2个水电站则高达16×106次，计算任务呈指数迅速增长，突显“维数灾”问题。因此，考虑到递推公式求解的天然并行性，可以对单时段内所有离散变量组合（St，Qt，Nt）的返回值计算实现并行化。(www.xing528.com)

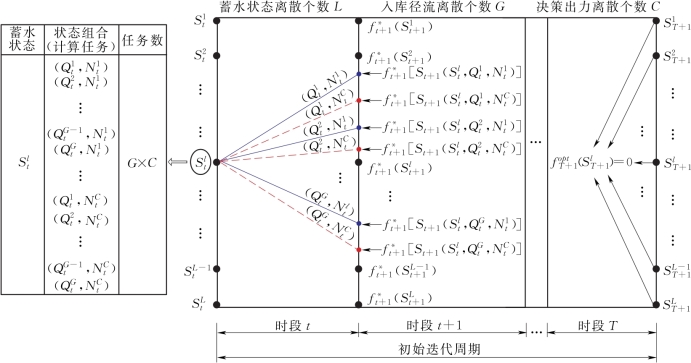
图9.3　单库最优决策出力递推过程示意图