并行方法设计优化

通过对DDDP方法的并行性分析，每次廊道优化迭代内所有离散变量组合在递推公式中的求解计算任务是独立可并行的。因此，DDDP的并行化可采用计算任务多阶段并行方式，即将每次廊道内迭代计算的所有变量组合作为父任务，其他过程为串行计算，比如初始解生成、廊道内最优轨迹确定以及廊道更替循环等。由于DDDP方法需要多次在廊道内迭代优化，本章提出的PDDDP算法将在求解过程中通过线程池的调用实现并行计算的反复执行。

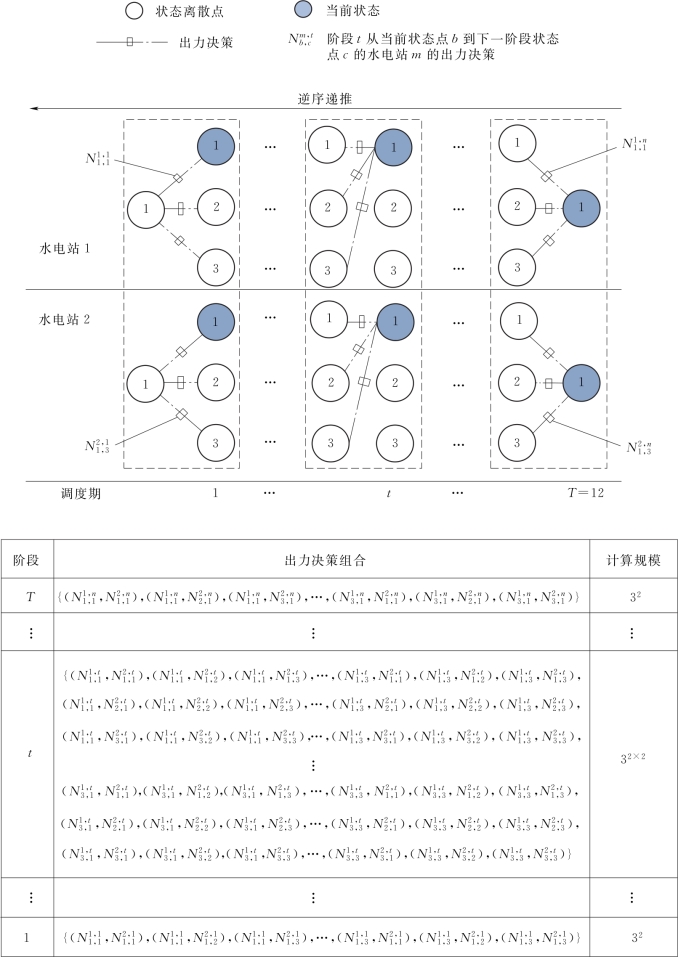
图8.5　3个离散点DDDP一次迭代计算规模示意图

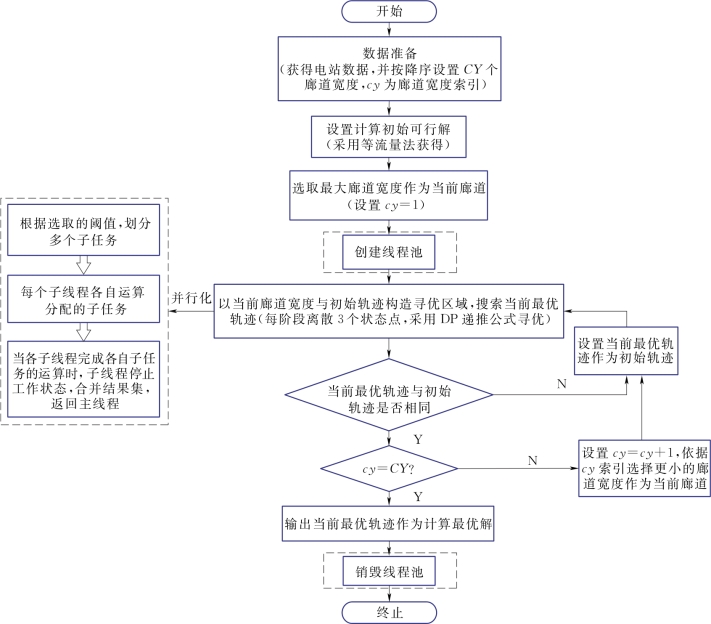
为了避免反复创建和关闭线程带来的巨大开销，在算法开始阶段创建线程池，并且在优化结束之后销毁。另外，在并行计算开始之前，需要根据参与计算的电站数目以及各个变量的离散数确定父任务的计算规模。PDDDP的父任务计算规模为3M＋（T-2）×32M＋3M，再结合应用配置的核数利用式（3.1）计算分解任务的阈值。图8.6为PDDDP算法流程图，除计算任务并行阶段步骤与串行方法有所区别外，其他过程与串行方法完全相同。

(www.xing528.com)

图8.6　PDDDP算法流程图

并行计算阶段流程如下：

第一步：划分子任务。从主线程中获取当前父任务的计算规模以及状态组合，并根据阈值划分为多个规模更小的计算子任务。为了便于父任务的递归分解，本章采用任务规模逐次对半方式分解，即每次父任务的递归分解产生两个计算规模相同的子任务。当子任务的计算规模小于或等于阈值时，停止任务的递归分解，分配各个子任务在不同的线程上同时进行计算。

第二步：子线程同时计算各自分配的子任务。每个分配到子线程的子任务由多个不同的状态组合构成，采用以水定电方法计算各组合下的返回值，包括出力、发电流量、弃水等指标。为了确保各线程之间的计算不会出现数据相关，需保证各线程之间的计算数据相互独立。计算数据主要包括静态数据与动态数据。静态数据不会造成子线程之间数据相关，直接从主线程中调用；动态数据包括各电站的计算水位、出力以及各变量组合的返回值等，则在各个线程中单独定义。

第三步：各子线程的返回值储存在各自的结果集中，当工作线程完成所有子任务的计算，将各子任务的结果集合并，返回主线程。