动态规划：多阶段决策方法

动态规划（Dynamic Programming，简称DP）最早于20世纪50年代初由美国数学家Bellman[46]提出，是目前水库群优化调度中应用最为广泛的优化方法，此方法对目标函数和约束条件没有严格的要求，数学模型和求解方法比较灵活，无论系统是连续的或离散的、线性或非线性的、确定性的或随机性的，只要能构成多阶段决策过程，便可用此方法求解。运用DP求解关键在于正确地写出基本的递推关系式和恰当的边界条件；须将问题的过程分成几个相互联系的阶段，恰当地选取状态变量和决策变量及定义最优值函数，从而把一个大问题转化成一组同类型的子问题，然后逐个求解，即从边界条件开始，逐段递推寻优，在每一个子问题的求解中，均利用了它前面的子问题的最优化结果，依次进行，最后一个子问题所得的最优解，就是整个问题的最优解。该方法主要涉及以下八个重要概念，如图8.1所示。

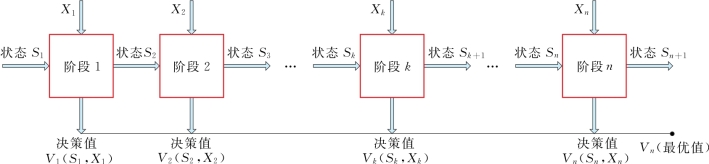
图8.1　动态规划方法多阶段决策示意图

1.阶段变量n

把一个问题的过程，恰当地分为若干个相互联系的阶段，则描述阶段的变量称为阶段变量。阶段的划分，一般可根据时间和空间的自然特征进行，但要便于问题转化为多阶段决策。

2.状态变量Sn

状态变量表示每个阶段开始所处的自然状况和客观条件。通常一个阶段有若干个状态，描述过程状态的变量称为状态变量。状态变量的取值有一定的允许集合或范围，称为状态允许集合。

3.决策变量Vn

决策变量表示当过程处于某一阶段的某个状态时可以作出不同的决定，从而确定下一阶段的状态，这种描述决策的变量称为决策变量。在实际问题中决策变量的取值往往在某一范围内，此范围称为允许决策集合。

4.多阶段决策过程

可以在各个阶段进行决策，去控制过程发展的多段过程，其发展时通过一系列状态转移来实现。系统在某一阶段的状态转移不但与系统当前状态和决策有关，而且还与系统过去的历史状态和决策相关。(www.xing528.com)

5.无后效性

若某阶段状态确定后，则在这个阶段以后过程的发展不受这个阶段以前各段状态的影响。若状态变量不能满足无后效性要求，应适当地改变状态的定义或规定方法。

6.策略

策略是一个按顺序排列的决策组合的集合。在实际问题中，可供选择的策略有一定的范围称为允许策略集合。从允许策略集合中找出达到最优效果的策略称为最优策略。

7.状态转移方程

状态转移方程是确定过程由一个状态到另一个状态的演变过程，描述了状态转移规律。

8.指标函数和最优值函数

指标函数是用来衡量所实现过程优劣的一种数量指标，称为指标函数。指标函数的最优值，称为最优值函数。

在梯级水库群优化调度中，以调度期内发电量最大为优化目标，递推方程表达式以及状态转移方程分别见式（8.1）、式（8.2），即

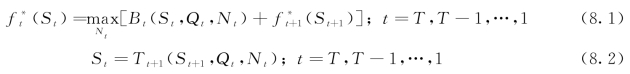
式中：t、T分别为时段序号和时段数；St、Qt、Nt分别为M维（电站个数）水电站库容、入库流量、出力，均为矢量；f*t（St）为时段t状态为St时，从时段t到末时段的系统最大发电量，亿kW·h；Bt（St，Qt，Nt）为时段t初始蓄水状态为St，入库流量为Qt，决策出力为Nt时的本时段系统发电量，亿kW·h；Tt＋1（St＋1，Qt，Nt）为时段t＋1到t的状态转移方程，通常为水量平衡方程，见4.2.2节中式（4.5）。