基于遗传算法的施工网络进度优化理论

1.遗传算法 (GA) 的思想

1971年,美国密执安大学的心理学、电工学及计算机科学教授John H.Holland提出了一种全新的、风格极不同于传统寻优算法的算法——遗传算法 (或简称GA,其思想基于达尔文的进化论与孟德尔的遗传学原理)。

GA 是一种仿生学算法,其收敛性没有绝对的保证,然而事实证明GA 是一种非常有效的算法,具有优越的性能,尤其适合于复杂问题的求解。求解一个优化问题时,将操作变量(自变量)表示成 “染色体”,在计算机上一般用二进制码串,例如:19 (十进制)=1×24+0×23+0×22+1×21+1×20=10011 (二进制),选择一群(Population)“染色体”——个体 (Individuals),将它们置于问题的 “环境” (约束)中,对它们进行交叉、变异、再生等“基因操作”,淘汰对环境适应性差的“染色体”,保留对环境适应值高的 “染色体”,反复操作,筛选出最适个体,从而求出问题的解。其相应的结构图如图3-8所示。

2.遗传算法的特点

因为利用了生物学中的进化论思想与遗传学原理,GA 是一种与传统寻优算法极不相同的算法,因而有许多不同于传统寻优算法的特点,具体来说,它在解优化问题时有以下四大优点。

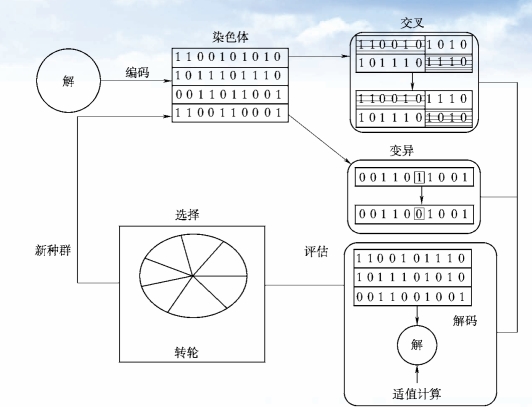
图3-8　遗传算法的一般结构

(1)遗传算法对所解的优化问题没有太多的数学要求。由于它的进化特性,它在解的搜索中不需要了解问题的内在性质。

(2)进化算子的各态历经性使得遗传算法能够非常有效地进行概率意义下的全局搜索,而传统的优化方法则是通过邻近点比较而移向较好点,从而达到收敛的局部搜索过程。这样,只有问题具有凸性时才能找到全局最优解,因为这时任何局部解都是全局最优解。(www.xing528.com)

(3)遗传算法对各种特殊问题可以提供极大的灵活性来混合构造领域独立的启发式,从而保证算法的有效性。

(4)它的搜索始终遍及整个解空间,能找到近乎全局最优解,因而在工程正网络计划优化方面具有广泛的应用价值。

3.设计GA 的基本步骤与优化算法描述

(1)确定编码方案,GA 求解问题不是直接作用在问题的解空间上,而是利用解的某种编码表示。

(2)确定适应函数,是对解的质量的一种度量,通常依赖于解的行为与环境 (即种群)的关系,一般以目标函数或费用函数的形式来表示。

(3)确定选择策略,优胜劣汰的选择机制使适应值大的解有较高的存活率。

(4)选取控制参数,控制参数主要包括种群的规模、算法执行的最大代数、执行不同遗传操作的概率,以及其他一些辅助性控制参数。

(5)设计遗传算子,遗传算子主要包括再生、杂交、变异,以及其他高级操作。

(6)确定算法的终止准则,由于GA 没有利用目标函数的梯度等信息,所以在演化过程中无法确定个体在解空间中的位置,因而无法用传统方法判定算法收敛与否,以便终止算法。常用的办法是,预先定个最大的演化代数,或算法在连续多少代解的适应值没有明显改进即终止。