串联电阻、电感、电容电路

在分析实际电路时，我们一般将复杂电路抽象为由若干理想电路元件串并联组成的典型电路模型进行简化处理。本节讨论的RLC串联电路就是一种典型电路，从中引出的一些概念与结论可用于各种复杂的交流电路，而单一参数电路、RL串联电路、RC串联电路则可看成是它的特例。

1.电压与电流之间的关系

图1-35a所示为RLC串联电路。

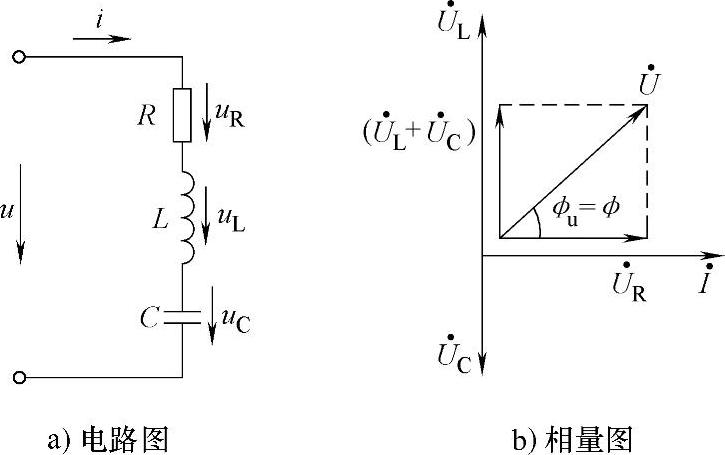
图1-35 RLC串联的交流电路

设有正弦电流i=I_msinωt通过RLC串联电路，根据上一节的分析，该电流在电阻、电感和电容上的电压降分别为

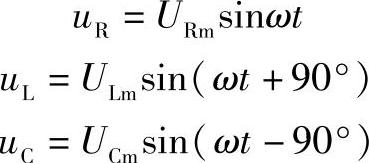
根据基尔霍夫电压定律，总电压为

u=u_R+u_L+u_C

用相量形式表示为

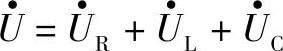
现用相量表示法讨论u、i的有效值关系及相位关系。以为参考相量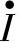，=I∠0°，则

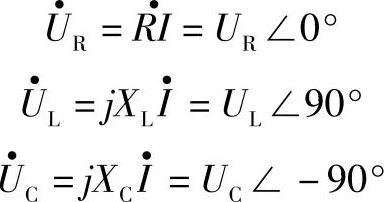
作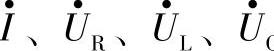的相量图，如图1-35b所示。

（1）电压有效值

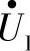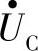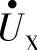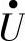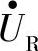将与的相量和定义为，由相量图可知外接电压相量、相量与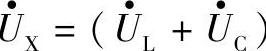构成一个直角三角形，称为电压三角形，如图1-36a所示。

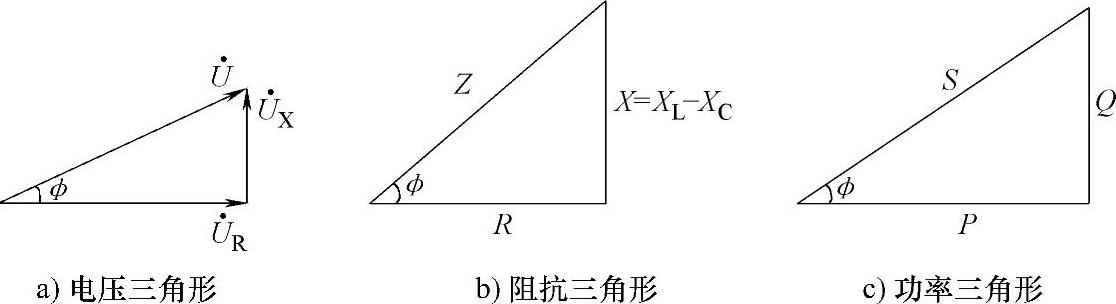
图1-36 电压、阻抗及功率三角形

不难求出：

将U_R=RI，U_L=X_L I，U_C=X_C I代入式（1-32），得

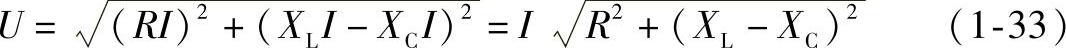
根式R²+（X_L-X_C）2具有阻碍电流的性质，称为电路的阻抗，用符号|Z|表示，它的单位也是欧姆（Ω），即

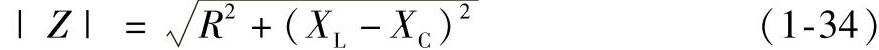
（2）电压u与电流i有效值之间的关系

阻抗中的（X_L-X_C）被称为电抗，用符号X表示，将X=X_L-X_C代入式（1-33），有

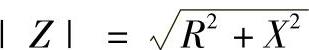
阻抗|Z|、R与X的关系也可用直角三角形表示，称为阻抗三角形，如图1-36b所示。于是，电压电流有效值关系为U=|Z|I。

（3）电压u与电流i的相位差由于以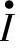为参考相量，ϕ_i=0，所以u、i的相位差ϕ=ϕ_u-ϕ_i=ϕ_u，由电压三角形可知

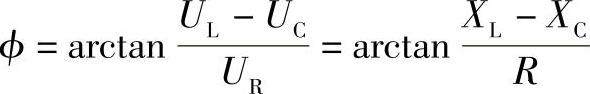
可见，当电源频率一定时，电压u与电流i的相位关系和有效值关系都取决于电路参数R、L、C。

（4）电压u与电流i的相量关系

由单一参数电路的电压关系可得

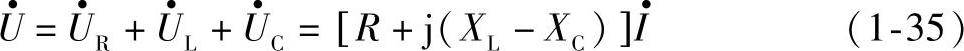
式中R+j（X_L-X_C）称为复阻抗，用符号Z表示，即

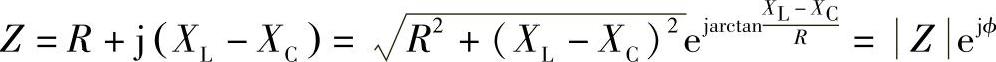(https://www.xing528.com)

式中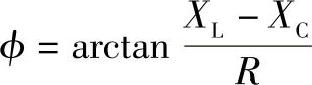是复阻抗的辐角，也称阻抗角，它决定了R、L、C串联电路中u、i的相位差。复阻抗是一个复数，具有大小和角度，但它不是表示正弦量的相量，所以其上方不加点。有了复阻抗的概念，则式（1-35）可写成

式（1-36）与直流电路中的欧姆定律有相似的形式，称为欧姆定律的相量形式。进一步展开推导，有

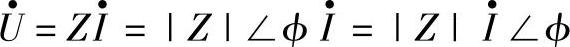
可见，式（1-36）既表达了电路中电压与电流有效值之间的关系U=|Z|I，又表达了电压与电流之间的相位差ϕ。若ϕ>0，说明电压超前电流ϕ角，这种电路称为感性电路；若ϕ<0，说明电压滞后于电流ϕ角，这种电路称为容性电路；若ϕ=0，说明电压与电流同相位，这种电路称为电阻性电路。

2.电阻、电感、电容串联电路的功率

在分析单一参数电路元件的交流电路时已经知道，电阻是消耗能量的，而电感和电容是不消耗能量的，在R、L、C串联电路中能量的交换情况是怎样的，电路的功率又是如何计算的，这些便是下面要讨论的问题。

（1）平均功率（有功功率）

在R、L、C串联的正弦交流电路中，若u、i参考方向一致，且设有正弦电流i=I_msinωt通过，则电压U_m=sin（ωt+ϕ），电路的瞬时功率为

P=ui=I_msinωt×U_msin（ωt+ϕ）

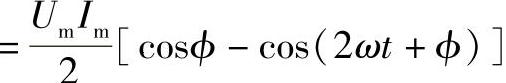
=UIcosϕ-UIcos（2ωt+ϕ）

电路的平均功率为

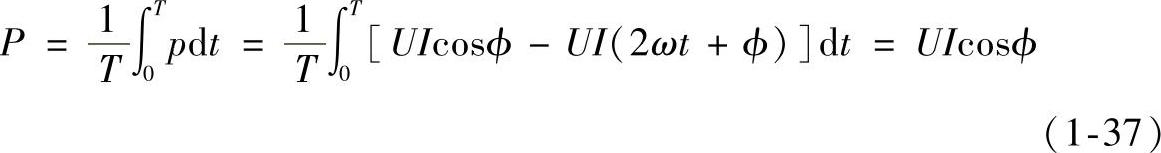
式中ϕ———电压u与电流i的相位差，cosϕ被称为功率因数，这时ϕ

又被称为功率因数角。由电压三角形可知Ucosϕ=U_R，

所以

P=UIcosϕ=U_RI=RI² （1-38）

式（1-38）说明R、L、C串联的正弦交流电路的平均功率就是电阻元件消耗的平均功率，因为电感元件和电容元件的平均功率为零。这为以后求解复杂电路的有功功率提供了理论根据。

（2）无功功率

在R、L、C串联的正弦交流电路中，电感元件的瞬时功率为p_L=u_Li，电容元件的瞬时功率为p_C=u_Ci。由于电压u_L和u_C反相，因此当p_L为正值时，p_C为负值，即电感元件取用能量时，电容元件正放出能量；反之，当p_L为负值时，p_C为正值，即电感元件放出能量时，电容元件正取用能量，因此R、L、C串联的正弦交流电路中的无功功率为

Q=Q_L-Q_C

由于Q_L=U_LI，Q_C=U_CI，所以

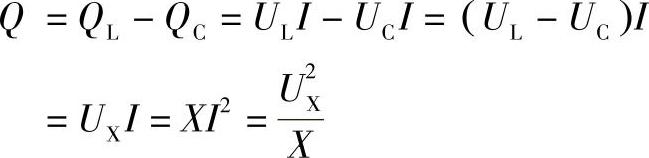
由电压三角形可知U_X=Usinϕ，故

Q=UIsinϕ （1-39）

对于感性电路，X_L>X_C，则Q=Q_L-Q_C>0；对于容性电路，X_L<X_C，则Q=Q_L-Q_C<0。为了计算的方便，有时直接把容性电路的无功功率取为负值。例如，一个电容元件的无功功率为Q=-Q_C=-U_CI。

（3）视在功率

在正弦交流电路中，把电流电压有效值的乘积定义为视在功率，用S表示，即

S=UI （1-40）

为了与平均功率相区别，视在功率不用瓦作单位，而用伏安（V·A）作单位。

由图1-36c功率三角形可知P、Q、S三者均成直角三角形，故：

P、Q、S三者也构成直角三角形，称为功率三角形，如图1-36c所示。